论文总字数:14215字
目 录
1引言.....................................................1
2麦克斯韦方程的含义,电磁场分布以及传播...................7
3求解麦克斯韦方程.........................................9
3.1 方法一 FDTD
3.2 方法二 FEM
4 严格耦合波分析........................................16
5 具体实例...............................................18
6 总结...................................................23
参考文献
致谢
时域有限差分法求解Maxwell方程的应用
李公度
,China
Abstract: Based on the understanding of the Maxwell equations, the solution of Maxwell's equations of the three methods, namely the finite difference time domain (FDTD) and finite element (FEM) and rigorous coupled wave analysis method. FDTD method using alternating sampling method for electromagnetic field E, H components are discrete in time and space, each of the four H or E field of a E or H components are surrounded by using the discrete mode four to one transformation of the Maxwell equation containing time variable for the differential equation, and the solution. The finite element method is to discretize the differential equations, to process the data on each grid point, and finally to form the differential equations of the continuum by means of the set method. Rigorous coupled wave analysis (RCWA) is based on a Maxwell equation on the theory of form of vector diffraction modeling, using Fourier series of grating region of the dielectric constant and electromagnetic field, so as to obtain the coupled wave equation, in the results after evaluation is obtained after the diffraction efficiency.
Key word:Finite difference time domain; Maxwell equations; finite element method
引 言
时域有限差分法由K. S. Yee 在1966年被提出,他提出这个计算方法的基础就是最基本的麦克斯韦方程。在FDTD方法被提出以后,伴随计算技术,特别是电子计算技术的成长,FDTD方法获得了巨大的发展空间,在电磁学,光学等多个领域被广泛利用。
时域有限差分方法是由有限差分法发展出来的直接由麦克斯韦方程组对电磁场进行计算机模拟的数值分析方法,在此我们首先分析FDTD的几种特点。
1 FDTD适用于分析系统谐振点附近的很宽频带响应
2可以分析任意三维形状的问题
3适用于研究理想导体,实际金属和绝缘物体等各类物体在电磁波作用下的效应
4适用于处理具有频谱依赖性的煤质参量
5适用于阐明多种类型的反应,包含了远近场,如散射场,穿透,内耦合等。
6适用于分析雷电,EMP,HPM,雷达,激光器等激励源。
7适用于分析多种多样的体系,如烟雾或屏蔽,防护罩,飞机,卫星,探测等等。
其次FDTD的使用方向也越来越趋近于我们的生活,时域有限差分方法最适宜使用于对瞬态相应问题的分析,特别是在复杂的地理环境和复杂的几何环境下,例如埋地天线与介质覆盖天线等情况。
影响时域有限差分方法在实际生活中的应用因素也有很多方面,需要我们在使用时首要处理,比如单元尺寸大小,时间步长以及入射场布局,场强的计算,吸收边界条件以及资源的需要与供求方面等问题。
以上是对时域有限差分方法的介绍,本文是对利用FDTD对麦克斯韦方程进行求解的应用的讨论,那么麦式方程也是我们需要了解的一大部分。
麦克斯韦方程组并不是由麦克斯韦本人发现的,而是他在前人总结关于电磁现象基本规律的基础上提出的。奥斯特等人提出了电场与磁场的产生关系,而法拉第则提出了磁场产生电场的法拉第电磁感应定律。在这些前人所拥有的理论与实验基础上,麦克斯韦又进一步提出了“位移电流”的设想。在这基础上,他创造出了麦克斯韦方程组,由此电和磁达到了完全的结合,形成了具有重大意义的电磁场理论。这个方程组所要说明的问题可以简单的概括为两句话:“变化的磁场产生电场(法拉第电磁感应定律)”、“变化的电场产生磁场(位移电流假说)”。
在介质中,麦克斯韦方程组的微分形式为:
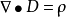
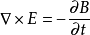
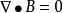
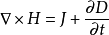
麦克斯韦利用这四个方程计算出了电磁波的传播速度,同时发现了电磁波的传播速度与光的传播速度相同。于是他大胆提出想法,那就是光的本质其实是电磁波,后来赫兹用实验证明了麦克斯韦的假设是正确的。
对于这个方程组,大部分人应该不太能理解。可它所带来的巨大的生活变革,相信大家在了解后都能从生活中感受到。比如我们所用的手机,无线电通话技术等。电动力学就是通过这个方程组进行研究,从而得出相应的应用,进而推动人类的发展。
从对麦克斯韦方程组的研究,可以得到光波其实本质就是 电磁波。经典电磁学的基础方程也就建立在麦克斯韦方程组与洛伦兹力方程之上。在这些基础上发展出的现代的电力科技与电子科技正是带给我们无限的便捷的根本。
介绍完了时域有限差分方法与麦克斯韦方程组之后,我们就开始对利用FDTD对Maxwel方程组的求解进行讨论。
第二章 麦克斯韦方程
1 麦克斯韦方程的含义
麦克斯韦方程组是一个表现了时变电磁场中的基础性质的基本方程组,在时变电磁场中,电场与磁场相互作用,形成了一个不可分割的团体。在引言中,我们已经介绍了在介质中的麦克斯韦方程组的微分形式,在这里具体再一条条的介绍。
首先第一条 指的是电场的散度定律也就是电场的通量定律,既存在独立的电荷,无旋电场的电力线是起于正电荷,止于负电荷。表明了电荷产生了电场。
第二条 是电磁感应定律,处于变化中的磁场会产生感应电场,该电场对电荷会产生力的作用,同样静电场也是一样的结果,所不同的是感应电场沿闭合回路的作用效果不为零,性质与涡旋场相同,旋涡源是变化中的磁场,通过进一步的实验,证明只要闭合曲线内磁通量发生变化,不仅仅是导体回路上存在感应电场,非导体闭合回路上同样有电场的存在。
第三条 指的是磁场的散度定律,也就是磁通连续性原理以及不存在磁单级子,磁力线是闭合状态的。
第四条 指的是全电流定律,表示传导电流与位移电流相互作用从而表现出磁场的旋涡源,传导电流也就是由电荷的定向运动形成的电流,位移电流也就是电场随时间变化形成的电流即总电流密度。
2 麦克斯韦方程的电磁场分布
- 静电场中的麦克斯韦方程分布
在静电场的环境下,电场与磁场不再结合,所以电场中的麦克斯韦方程组变为
=0 =
静电场E变为保守场,故引用电标势来描述它。但是在许多实际问题中,自由电荷只在一些导体或是介质的表面出现,空间里没有更多的自由电荷的分布,所以在这种情况下我们利用介质的表面作为区域的边界,在介质或者导体的内部是不存在自由电荷的,即自由电荷面密度为0,由此可得到拉普拉斯方程。这时问题就简化为求拉普拉斯方程中满足利用介质表面作为区域边界的解。
求静电场中的麦克斯韦方程组的分布的思路为首先求满足电荷分布的泊松方程的解,然后当电荷只在导体或者介质的表面时,求拉普拉斯方程中满足此条件的解。
(2) 静磁场中的麦克斯韦方程分布
在静磁场中,因为是由恒定电流所激发的环境,电场和磁场不会发生直接的关系,所以静磁场中的麦克斯韦方程变为
由 可知可以用磁失势的旋度来表示该磁场 。即,把该式代入可以得出用方程表示的磁失势为 ,这样就可以通过求满足电流分布的磁失势的方程的解来解决静磁场的问题。所以解决静磁场中的电磁方程的思路为,先求得满足电流分布的磁失势方程,在J=0的区域中,麦克斯韦方程变为,由此引入磁标势从而磁场中的泊松方程可写为。
- 自由空间中的麦克斯韦方程分布
在自由空间中,J=0且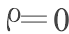 ,从而麦克斯韦方程变为
,从而麦克斯韦方程变为
剩余内容已隐藏,请支付后下载全文,论文总字数:14215字
相关图片展示:

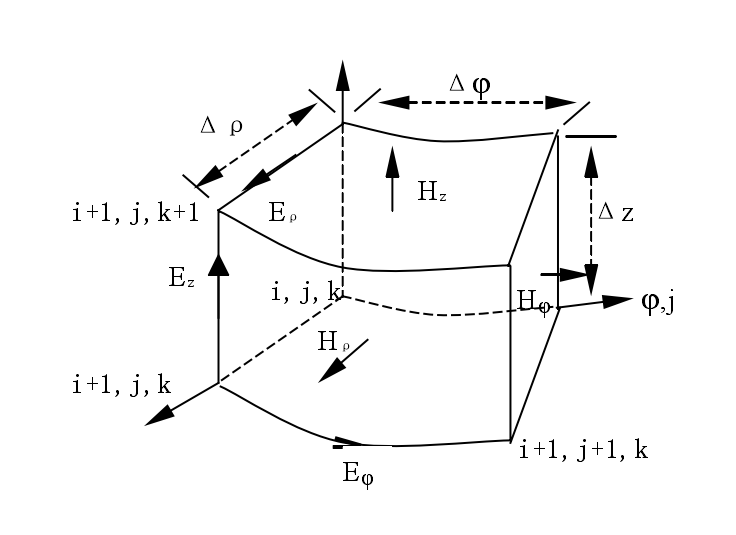

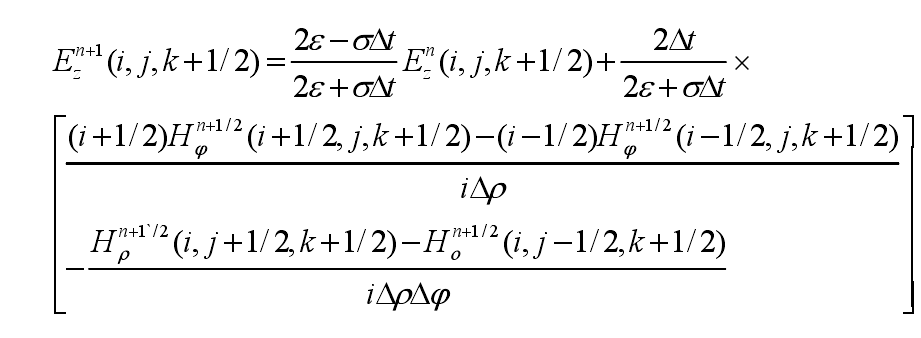

该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


