论文总字数：18736字

目 录

摘要 1

Abstract: 2

1 绪论 3

1.1 课题背景及其研究意义 3

1.2 国内外相关研究进展 3

1.3 研究内容及论文结构 4

2 经验模式分解（EMD）法原理 4

2.1 瞬时频率 4

2.2本征模函数（Intrinsic Mode Functions, IMF） 5

2.3 EMD方法分解过程 5

2.4 EMD信号分解实例 7

3 二维经验模式分解（BEMD）方法及其实现 8

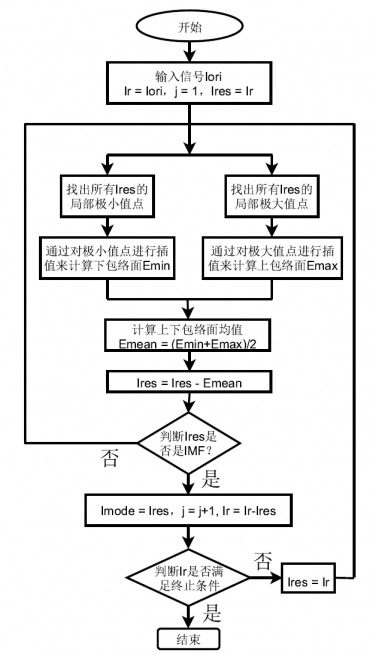
3.1 二维EMD分解流程 8

3.2 极值点的选取 9

3.3 曲面插值方法 9

3.3.1 分散数据插值 9

3.3.2 径向基函数（Radial basis function）曲面插值 10

3.3.3 多级B样条的曲面插值 10

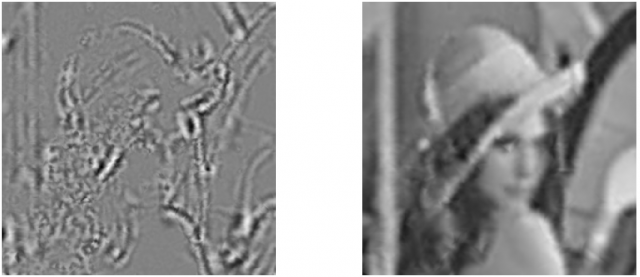
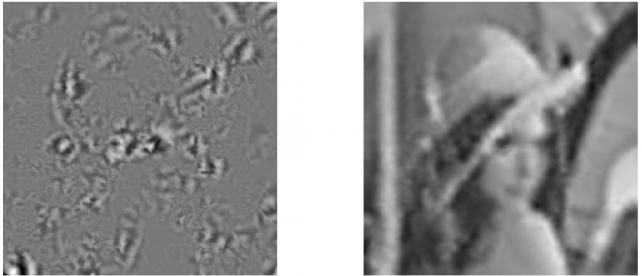
3.4 图像分解实例 11

4 二维经验模式分解在图像滤波中的应用 12

4.1基于BEMD的滤波方法 12

4.1.1 阈值法 12

4.1.2 部分IMF重构方法 13

4.2 图像滤波结果分析 14

4.3 与其他滤波方法效果比较 20

5 总结与展望 22

5.1 本文工作总结 22

5.2 EMD方法的展望 22

参考文献 23

致谢 24

基于EMD的图像滤波研究与实现

茅威

, China

Abstract: Image filtering plays an important role in the digital image processing, relating to environmental science, physics, biology and other disciplines and it is widely used in Image recognition, meteorological environment monitoring and other fields. In 1998, Norden E. Huang proposed a new analysis method with multi-scale multi-resolution characteristics called the empirical mode decomposition method. This method has a good effect on non-linear and non-stationary signals. Subsequently, the French scholar Nunes proposed the bidimesional dimensional empirical mode decomposition method based on the one-dimensional empirical mode, and then the method was applied to image filtering and other aspects.

The main work of this paper are as follows:

1. Introduce the basic concept of one-dimensional EMD method and its principle, then expound the 2d EMD method on the basis of one dimension, give its relevant algorithm steps, and then decompose the image.

2. Study the filtering algorithm based on EMD method, and use MATLAB software to write relevant codes.

3. Filter the noise image with this filtering method and analyze its denoising effect. And then analyze the advantages of the EMD method compared with traditional filter analysis method.

Key words: Empirical Mode Decomposition (EMD); Bidimensional Empirical Mode Decomposition (BEMD); Intrinsic Mode Functions (IMF); Image filtering

1 绪论

课题背景及其研究意义

1822年，法国数学家傅里叶在研究热传导理论时发表了“热的分析理论”著作，提出了傅里叶信号分析方法。[1]傅里叶变换方法搭建了时域分析和频域分析之间的桥梁。研究表明，某些事物的本质往往可以通过信号的频率来进行表示。正因如此，傅里叶分析方法在信号分析中才显得如此重要，该方法在信号分析中已经达到了不可或缺的地步。

傅立叶分析理论在信号分析理论发展过程中起到了重要作用。但是随着进一步的研究，人们注意到傅立叶变换其实是一种整体积分变换。它存在着一对矛盾：时域和频域的局部化的矛盾，即要想在时域上得到信号足够精确的信息，就得不到信号在频域上的信息，反之亦然。另外，傅立叶变换是一种典型的线性稳态变换，因此，傅立叶分析适合分析频率不随时间变化的线性平稳信号，以及对信号做全局分析；不适合频率随时间变化的非线性、非平稳信号，以及对信号作局部分析。[2]为了解决这对基本矛盾，许多研究人员在不同领域进行了相应的探索，一部分研究者将时间和频率分析结合起来分析，提出了诸如短时傅里叶变换（Short Time Fourier Transform, STFT）、盖伯变换和小波变换等。然而，这些时频分析方法的本质还是基于傅里叶分析理论的，其中小波变换还依赖于其基函数的选取，缺乏自适应性，容易出现多余信号，而且受海森堡测不准定律的限制，这些方法并不能精确描述频率随时间的变化。

1998年，美国华裔科学家黄锷（N. E. Huang）等人在美国国家宇航局创造性地提出了一种信号处理方法——经验模式分解（Empirical Mode Decomposition, EMD）法。EMD方法最大的特点就是其基函数来自信号自身，因此，与其他传统方法相比较，这种分析方法具有自适应性。[3]EMD基于信号的各种内在时间尺度相关的能量从较细的时间尺度（高频模式）开始到较粗的时间尺度（低频模式）进行连续提取。由于该方法多尺度多分辨率的特性，该方法可以很好地处理非线性非平稳信号。

1.2 国内外相关研究进展

经验模式分解（EMD）法作为一种全新的用于处理非线性非平稳信号的分析方法具有独特的优势，该方法起初主要用于信号分析和故障判断等应用层面。随后，法国学者J. C. Nunes等人于2003年利用数学形态学中的形体重建算子和径向基函数（Radial Basis Function, RBF）提出了一个二维筛分过程来进行纹理提取，实现了EMD方法从一维到二维的扩展，实现了真正意义上的二维经验模式分解（Bidimensional Empirical Mode Decomposition, BEMD）。[4]

自从BEMD分解方法被提出之后，人们开始将其应用到图像处理领域，取得了较好的成果。例如，2005年，沈滨、崔峰、彭思龙等人利用BEMD方法将图像进行分解得到包含不同空间尺度的本征模函数（IMF），从而实现图像纹理的提取。中科院的刘忠轩等人提出了一种称为方向EMD的新BEMD框架，并利用DEMD进行图像纹理分割。2010年，梁灵飞提出了一种新的经验模式分解方法——窗口经验模式分解（Window Empirical Mode Decomposition, WEMD）法，并利用WEMD进行图像边缘检测、图像滤波等得到了较好的结果。[5]

图像处理现已成为一门非常热门的学科，其应用非常广泛，例如视频影像处理、医学图像处理、气象遥感图像处理等方面。图像的基本特性之一就是其具有多尺度的特点，而二维EMD方法由于其多尺度多分辨率的特点，在图像处理领域有着其独特的优势。今后该方法还有待人们的进一步研究，在图像处理领域发挥更大的作用。

研究内容及论文结构

本文主要研究EMD及其二维推广（BEMD）的原理和实现方法并以此为基础进行图像滤波研究。本篇论文总共分为五个章节，主要研究内容如下：

第一章主要介绍本文研究内容的背景意义，介绍经验模式分解法在国内外相关研究进展。

第二章主要阐述了EMD方法的基本原理，介绍了EMD相关的概念如瞬时频率、本征模函数等，然后进行信号分解实例分析。

第三章介绍二维EMD方法的基本原理，然后介绍该方法的具体步骤，以此来进行图像的实例分解。

第四章主要利用二维EMD法进行图像滤波处理，介绍图像滤波降噪的原理，然后对图像滤波效果进行分析并与其它滤波方法相比较，总结二维EMD方法的效果。

第五章对本文所做的研究进行全面的总结，指出EMD方法的不足之处，对此进行展望。

2 经验模式分解（EMD）法原理

2.1 瞬时频率

虽然对于瞬时能量等概念人们已经广泛认可，但是人们却不太愿意接受瞬时频率这一概念。接受瞬时频率的想法有两个基本困难：第一个受到傅里叶频谱分析理论的影响，并且在传统傅里叶分析中，频率由具有固定幅度的正弦或余弦函数定义，该幅度跨越整个长度作为该定义的扩展，我们获得的瞬时频率也必须与正弦或余弦函数相关。因此，我们至少需要一个正弦波或余弦波的完整振荡来精确定义局部频率值。根据这个理论，就没有比全波更短的波了。这个定义对频率值经常改变的非平稳数据没有意义。第二个难点是我们不能以统一的方式定义瞬时频率。尽管如此，由于引入了通过希尔伯特变换进行数据分析的手段，这种困难已经不再是障碍了。[12]

对于任意时间序列，我们可以进行希尔伯特变换，

剩余内容已隐藏，请支付后下载全文，论文总字数：18736字

相关图片展示：