一类随机传染病模型的数值模拟

论文总字数：44613字

摘 要

随机传染病模型是通过运用随机微分方程的理论对传染病建立的数学模型。该模型主要致力于对加入随机因素的传染病的描述，揭示传染病发展和传播的规律，追踪与疾病流行有关的各种因素。本文主要讨论一类在确定性系统中加入随机扰动的随机传染病模型，对随机系统进行动力学分析，最后得到白噪声强度与随机模型解的稳定性的关系。

第一章介绍了传染病模型研究的重要意义和相关背景， 及近年来随机传染病模型的研究现状，简单地介绍了如何对模型加入随机干扰，以及本文所要研究的模型

第二章介绍了本文的研究工作所要了解的一些基本定义与定理。

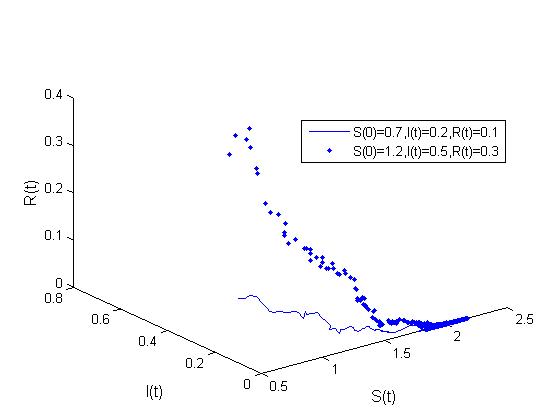
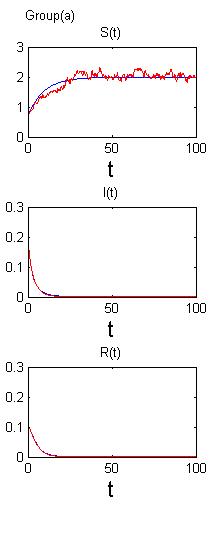
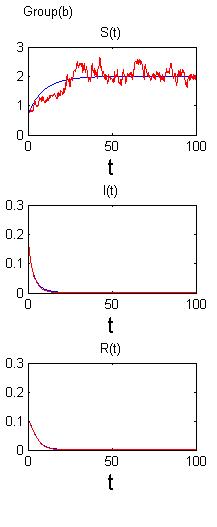
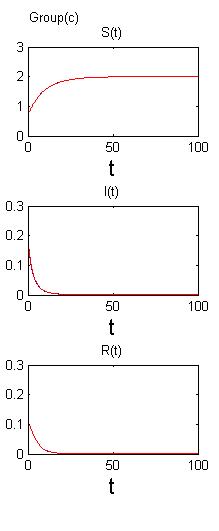
第三章，利用在确定性模型加入随机扰动建立随机SIRS模型，并用停时分析的方法给出了模型正解具备唯一性和全局性的证明。我们再分别讨论当基本再生数大于或小于等于1时模型的动力学行为。如果，随机模型的解将会在无病平衡点附近做随机振动，如果，随机模型的解将会在地方病平衡点做随机振动。最后对上述模型进行计算机模拟来验证研究的理论成果。

第四章，对本文的分析和研究成果提出总结和对今后研究前景。

关键词：随机微分方程；随机传染病模型；伊藤公式；Lyapunov 函数

Abstract

Stochastic epidemic model is a mathematical modeling method which established by applying the theory of stochastic differential equations about infectious disease. This model focuses on description of infectious disease with stochastic factors, the development and spread of infectious diseases, and tracing factors that are responsible for or contribute to their occurrence. In this paper, stochastic epidemic models were modified by introduce random perturbations in the deterministic models. Based on the theorey of dynamics for the stochastic epidemic model, relationship between the intensity of white noise and the stability of the solutions of stochastic model is obtained.

In the first chapter, we introduce the background and significance of the epidemic model and research status of stochastic epidemic model. Then we mention different possible approaches to include random perturbations in the studied epidemic models.

In the second chapter, we introduce the preliminary knowledge which will be used in this paper.

In the third chapter, we establish a stochastic SIRS model by including random perturbations in the deterministic model and show that the stochastic SIRS model has unique global positive solutions by stopping time. We find that the dynamic property of this model was determined by the basic reproduction number . When , the solution of the model is under random vibration around the disease-free equilibrium of the deterministic model; when , the solution of the model is under random vibration around the endemic equilibrium of the deterministic model. Finally, numeric simulation is given to verify the conclusion.

In the fourth chapter, we make a summary and outlook of this research work in the future.

Keywords: Stochastic differential equation; Stochastic epidemic model; Ito formula; Lyapunov function

目录

摘要 i

Abstract ii

目录 iii

第一章 绪论 1

1.1 研究背景及意义1

1.2 随机传染病模型的研究现状1

1.3 本文的主要内容2

第二章 预备知识 4

2.1 基本定义4

2.2 基本定理5

第三章 一类随机传染病模型 7

3.1模型的建立7

3.2正解的全局唯一存在性8

3.3随机模型的解围绕无病平衡点的渐近行为9

3.4随机模型的解围绕地方病平衡点的渐近行为11

3.5数值模拟15

第四章 总结与展望 21

致谢 22

附录 23

参考文献 42

第一章 绪论

• 1. 研究背景及意义

由于科学研究不断深入，在1940年左右，随机微分方程开始逐渐发展起来成为一门交叉学科。随机微分方程是微分方程的扩展，最早的概念由爱因斯坦提出，主要考虑的是噪声用Brown运动建模的模型。之后由保罗继续这项学科的研究。此后伊藤清和鲁斯兰斯特拉托诺维奇对该领域进行了补充和完善，使之成为一个新的研究领域。随机微分方程主要用来对现实世界中的随机现象进行描述和建模，例如统计物理、股票模型中都有应用。在最近50年，许多专家对随机微分方程各类性质和现实模拟做了很多的研究，如文献[1-4]。

传染病学是研究疾病传播的科学，目的在于追踪与疾病流行有关的各种因素。现阶段在大部分的流行病研究中，研究人员需要运用各类数学模型对流行病进行描述和建模。因此进一步出现了传染病动力学模型。在1927年，Kermack与McKendrick建立了最基本的SIR模型。现在所研究的传染病模型很大一部分都是以该模型为基础而建立的，参见[5]。

在确定性SIR模型中，已经有众多学者对SIR模型及其扩展进行了大量的研究分析，参见[6-13]。由于现实世界具有不可预测的随机性，确定性模型不能够满足我们对传染病的研究，需要在确定性模型的基础上建立更为复杂的模型，因此现在有很多学者在研究随机生物系统和随机传染病模型，参见[14-26]。在随机传染病模型中，需要考虑如何对模型加入随机因素，而用不同的形式加入随机因素的干扰将会产生不同的作用，所以随机传染病模型具有重要的意义。

• 1. 研究现状

由于传染病问题的分析需要各种数学模型及理论，因此大力推动传染病动力学的迅速发展。在1926 年，为了研究1666年左右发生在伦敦的鼠疫的传播规律以及1906 年发生在孟买的疫病的流传规律，Kermack和McKendrick建立了最基本的SIR模型[5]。通过对传染病仓室模型的研究，他们提出如果基本再生数流行病将会持续下去，而如果流行病则会在一段时间后灭绝。

传染病模型建立之初，大部分学者研究的是确定性系统，但是随着科学的发展，研究者发现世界具有不确定性，确定性模型不能够满足我们对传染病的分析，因此需要在确定性模型的基础上构建更为复杂的模型来研究传染病。例如在文献[26-28]中，作者考虑了模型参数的随机扰动。Dalal等人在文献[26]中，研究了在AIDS模型(使用了避孕套)中加入随机扰动，他们将参数替换为，其中是环境白噪声，是该白噪声的强度，于是变为与确定性AIDS系统相对应的随机系统。在文献中，作者得到了该随机系统具有唯一全局正解，且一方面感染群众将会在时间的变化中灭绝，另一方面易感者将会变得平稳。最后，证明了噪声项驱动系统几乎必然指数稳定和依概率稳定，但如果则不是p阶矩指数稳定的。在Dalal等人的另外一篇文章中，研究了一种HIV-1型艾滋病模型，该模型的死亡率与环境白噪声相关。一方面该模型具有非负解且被传染的病毒颗粒和细胞的个数几乎必然收敛到0，另一方面未被传染的细胞以概率1迫近一个均值回复随机过程。最后，他们进一步给出了此过程的方差以及其数学期望。在文献[28]中，Tornatore讨论了对流行病传播系数加入随机因素的随机SIR模型，再讨论该模型是否带有时滞时的动力学行为，提出了在模型中加入干扰后，该模型的再生数与确定性模型不一样，然后用解析与计算机模拟的方法得到了该模型的阈值。

在文献[30,25]中，研究了在传染病模型的地方病平衡点周围关于白噪声的随机波动。在文献[30]中，Beretta研究了一种特殊的流行病的传播模型。他们假设随机扰动类型为白噪声，对,,与,,的距离添加白噪声随机波动，从而影响,,。即下述随机模型

式中,,是确定性模型的正平衡点，为常数，是相互独立的标准Brown运动(i=1,2,3)。文献利用Lyapunov函数，阐明了当系数满足一定条件时条件随机模型依概率稳定。在文献[22]中，作者加入随机波动的方法与文献[30]相似。通过在平衡点附近作随机波动，作者扩展了一种在海洋生态环境中由噬菌体所导致的传染病模型，通过用解析和计算机模拟的方法，证明了新的随机系统的解是均方渐近稳定的这个结论。

在文献[17]中，Imhof和Walche考虑了另一种在生物模型引入随机扰动的方法。他们讨论了一个特殊的确定性的单一底物恒化器模型。此外，通过使用比较原理，他们发现所有物种具有持续性。最后，在该确定性系统中添加白噪声的影响，得到了下列随机系统

式中，相互独立的标准Brown运动。文献讨论了上述的随机微分方程，他们证明了确定性模型各个变量是持续的，而另一方面随机模型各个变量将会逐渐消失。

近半个世纪以来，众多专家构造了许多互不相同的随机传染病模型，而且分析和讨论这些模型的动力学性态，获得了丰富的理论结果。随机传染病模型主要是关于模型的解各种动力学特性的研究，用来分析流行病的发展过程，规律和原因。

• 1. 本文的主要内容

本文研究下列SIRS模型，其中加入随机扰动的方法与文献[14]中的方法相同。,

式中,,表示相互独立的标准Brown运动，表示该Brown运动强度。

第三章将应用停时分析的方法给出模型的正解具有全局存在性和唯一性的证明。我们

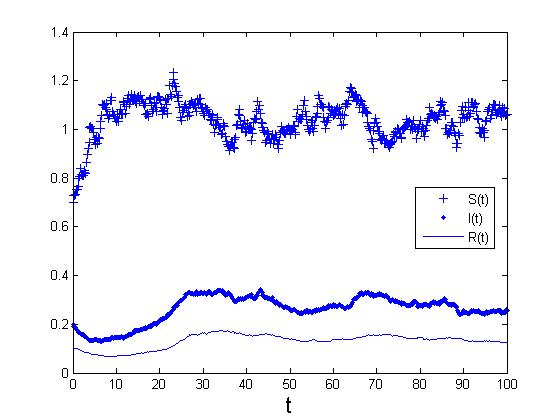
将分别讨论和的解的行为。当，只要满足一定条件，那么很小，因而系统存在稳定性。而在，我们将证明是有界的，且与白噪声强度有关，并且存在稳态分布。最后，我们将利用数值模拟来说明我们的发现。

第二章 预备知识

• 1. 基本定义

设为完备的概率空间，其中为上的一个代数且满足一定条件（单增，右连续，包含所有零测集）。是定义在这个概率空间上的布朗运动，。记，表示欧式范数。

考虑随机微分方程

(2.1)

其中初值，该方程和下列方程等价

(2.2)

定义 2.1.1[24] 解 若满足：

1. 是连续且为适应的；
2. ;
3. 方程(2.1)对于以概率1成立，

则称是随机方程(2.1)的解。

定义 2.1.2[2,24] 停时 设，是定义在上的非降代数族，是在上变化的随机变量，如果对，，则称是相对于的停时。

定义 2.1.3[2,24] Brown运动 设是n维适应随机过程，若满足：

1. 若，则是正定矩阵；
2. 若，则与独立；

则称是一个n维Brown运动或Winner过程。如果成立，称是n维标准Winner过程。

定义 2.1.4 白噪声 设是一个平稳时间序列，满足下列条件：

，

就称是一个白噪声。

定义 2.1.5[2,24] 微分算子 记为所有定义在上的非负函数所组成的族，是连续的，对x二次可导，对t一次可导。下列式子定义成随机微分方程(2.1)的算子

L作用于方程，得到

剩余内容已隐藏，请支付后下载全文，论文总字数：44613字

相关图片展示：