论文总字数:23785字
摘 要
本文详细阐述了微纳尺度的发展现状以及分子动力学模拟的内容,对采用分子动力学模拟研究纳米材料导热系数的原因,原理和方法给出了全面的介绍。选取典型纳米材料二氧化硅气凝胶作为研究对象并对其导热系数的研究现状给出了说明。鉴于气凝胶中气相导热比重很大,本文采用非平衡分子动力学模拟分别对自用空间下氩的导热情况和带有气凝胶骨架下氩的导热情况进行研究,并将两种导热情况进行对比。
根据对比,得到气凝胶独特的微纳孔隙结构是其低导热系数的重要原因。骨架的存在会影响内部气体的扩散并引起原子的漫反射,使得导热系数降低。
关键词:分子动力学模拟,非平衡态分子动力模拟,导热系数,纳米材料,二氧化硅气凝胶
MOLECULAR DYNAMICS SIMULATION ON THERMAL CONDUCTIVITY OF NANOMATER MATERIALS
Abstract
This paper elucidates the recent research of micro-scale thermal transport and the basic theory of molecular dynamics simulation. Besides, the basic theory, the detailed steps and the classification of molecular dynamics simulation on thermal conductivity are also discussed in this thesis. As one of the most representative nanometer materials, silica aerogel is chosen as the research objet. And in this paper, the recent research of thermal conductivity of silica aerogel is introduced as well. Since the gas phase play an important role in heat conduction, nonequilibrium molecular dynamics simulations were used to analysis the heat conduction of Argon in the free space as well as silica aerogel.
Through comparing the results, aerogel is of great significance for the low heat conductivity. The aerogel strictly confine the movements of gaseous molecules.
KEY WORDS: molecular dynamic, nonequilibrium molecular dynamics, thermal conductivity, nanometer materials, silica aerogel
目 录
摘 要 2
Abstract 2
第一章 绪 论 4
1.1. 研究背景 4
1.1.1. 纳微尺度的传热研究背景及发展 4
1.1.2. 二氧化硅气凝胶的基本介绍和应用 4
1.2. 二氧化硅气凝胶导热系数的研究进展和现状 4
1.3. 课题的研究内容 5
1.4. 分子动力学模拟方法简介 5
1.5. 分子动力学模拟的基本步骤 5
1.6. 导热系数的分子动力学模拟方法 7
1.6.1. 平衡态分子动力学模拟方法 8
1.6.2. 非平衡分子动力学方法 8
1.7. 分子动力学模拟的实现和基本软件介绍 11
第二章 自由空间下氩气导热系数的分子动力学模拟 12
2.1. 前言 12
2.2. 模拟模型 12
2.3. 无量纲化过程 13
2.4. 模拟方法 14
2.5. 模拟结果和分析 14
2.5.1. 速度自相关函数 14
2.5.2. 扩散系数 15
2.5.3. 径向分布函数 16
2.5.4. 导热系数 17
2.6. 本章小结 18
第三章 具有气凝胶骨架下的氩气的导热系数的分子动力学模拟 19
3.1 前言 19
3.2 骨架模型及模拟参数 19
3.3 模拟方法 21
3.4. 模拟结果 21
3.4.1. 速度自相关函数 21
3.4.2. 温度分布 21
3.4.3. 扩散系数 22
3.4.4. 导热系数 24
3.5. 本章小结 25
总结及展望 26
致 谢 27
- 绪 论
- 研究背景
- 纳微尺度的传热研究背景及发展
- 研究背景
微纳尺度的导热问题很早就进入研究范围,之后,随着研究的成熟,微纳的传热问题也开始设计对流和辐射方式。关于微尺度下的导热系数的问题可以追溯到20世纪30年代。随后,一些热物理学家注意到一系列工程器件中的传热问题的尺度效应,于是微纳尺度传热问题的研究由此开始。
到了80年代,由于计算机的快速发展和高密度微电子器件的冷却,使得全面了解特定尺度下热物性和热行为已成为很重要的工作重心。于是,在1997年,国际传热传质中心首次召开了微传热的国际会议,微尺度传热这一学科正式成立。
微尺度传热研究的重点所在是在时间和空间均微细化后,出现了很多与经典体系小不同的物理现象。原因可以分为两个方面,一个方面是连续介质的假设不再适用,另一类则是各种作用力相对重要性发生变化。因而对于导热系数来说,尺度效应成为一个很有挑战性的问题。
微尺度传热的需要从微观的能量入手,以便揭示材料微结构中的动量和能量运输机制。到现在为止,有以下四种方法适合研究微纳尺度下的传热和流动问题,分别是:量子分子动力学方法、 Boltzmann方程方法、Monte-Carlo模拟方法及分子动力学模拟方法。
微电子器械的利用和发展必然会成为以后经济的重要组成部分,相应的随着计算机科学快速,利用计算机科学计算研究微纳尺度传热问题会成为研究热点[[1]]。本文将讨论利用分子动力学模拟研究典型纳米材料的热物性,为微纳尺度传热研究提供基础研究参考。
- 二氧化硅气凝胶的基本介绍和应用
气凝胶通常是由纳米尺度的超微颗粒团簇形成的纳米多孔网络结构和网络结构中充满的气态物质组成的。气凝胶在常温下是固态物质,但是体积重近98%都是气体,所以密度很小,气凝胶外观透明,看起来和云一样,也因此被称为“固态烟”或者“冻住的烟”。
最常见的气凝胶为二氧化硅气凝胶。二氧化硅气凝胶是一种防热隔热性能都十分优秀的轻质纳米多孔非晶体固体材料,其孔隙高达80~99.8%。空洞的典型尺寸为1—100nm,比表面积为200~10000㎡/g,密度则低达3kg/m³,室温导热系数可低到0.012W/(mk)。正是由于这些特定使得气凝胶材料在热学,声学,微电子等方面均有广阔利用。
- 二氧化硅气凝胶导热系数的研究进展和现状
二氧化硅气凝胶导热系数的研究现有的方法有三种:分子动力学模拟、理论分析和实验研究。
实验研究方法可以很直接的得到所需要的数据,且速度快,可靠性好。常用的方法有:瞬态热带法、差式量计法和激光脉冲法。这些方法对实验仪器,实验条件的要求比较高,实验成本大。除此,由于是直接测量,对于对材料的导热机理无法有深入的认识。
理论分析方法也有很多进展, 在微观模型方面,Zeng[[2]]等提出了二氧化硅气凝胶的微观结构模型,给出了三种交叉立方阵列来描述气凝胶的骨架结构。并在研究过程中采用非晶二氧化硅材料的导热系数计算固相骨架的导热系数,得到的结果与实验数据相比是有出入的。魏高升[[3]]等通过探究微观结构特点,建立了一种气凝胶复合材料的微观模型,提出了一种可以描述材料内气固耦合导热的体传热模型。。BI[[4]]等采用动理论计算了颗粒单元的导热系数,在计算过程中考虑了初级粒子之间的界面热阻。张欣欣[[5]]等用分子运动论对二氧化硅气凝胶的传热机理进行了研究。但是,可以看出,由于理论分析是需要根据计算需要简化和假设,这样和实际情况就会存在误差,而且由于分析误差来源比较困难,得到的误差往往不可预计。
分子动力学方法很简单的说就是通过建立力场得到势场,然后建立分子的运动方程,并通过求解该方程得到分子的运输情况,以此可以模拟系统随时间变化的微观过程,并利用统计物理学的方法得到系统的宏观参数和输运特性。分子动力学方法仅需要分子/原子间的作用势函数,因为其更接近实际情况,而且直接从原子尺度入手,特别适用于研究纳米尺度范围内的热传递问题[[6]]。HUANG 等[[7]]采用非平衡分子动力学(Non-equilibrium molecular dynamics,NEMD)方法对比计算了晶态和非晶态二氧化硅纳米薄膜的导热系数,THOMAS[[8]] 等采用NEMD计算了非晶态二氧化硅纳米孔材料的导热系数。对于气凝胶内部的气相传热过程,研究较为成熟。刘育松[[9]]等采用Green-Kubo模型,借助分子动力学模拟的方法可以有效的研究气凝胶结构纳米孔隙内的氮气导热系数,证明了利用分子动力学模拟的方法可以有效地研究气凝胶内部的热传导。但其缺陷在于对于壁面的模型过于简单,没有真实的考虑二氧化硅结构的影响。郭雨含等结合现有实际结构参数,建立了气凝胶内部的微观结构模型,让分子动力学模拟更加细化,研究了气凝胶内部的导热特性。但对于气凝胶的固相骨架内的微观导热过程研究还不是很充分。苏高辉[[10]]等通过分子动力学模拟研究了二氧化硅气凝胶初级粒子导热系数,对气凝胶的固相传热的进一步研究提供很好的基础。
时至今日,对于二氧化硅的导热系数和传热机理,还没有比较完善的解释和说明[[11]]。所以,对于二氧化硅气凝胶导热系数的探究,就很有意义[[12]]。
- 课题的研究内容
SiO2气凝胶是一种典型的纳米多孔材料,它具有开放性的纳米孔隙和空间连续的网络结构。由于多空的问题使得其表观导热系数比较复杂,表面传热系数、气相导热系数、固相导热系数和辐射传热系数[[13]]都会影响其表观导热系数。因此要对三种传热机理分开并深入研究,最终能得到SiO2 气凝胶等效热导率。
本论文是二氧化硅气凝胶导热系数基础性研究。由于其导热系数的80%—90%[[14]]都是由气相导热系数影响,先针对孔隙中的气态物质建立模型,研究其导热性能以探究基本气凝胶的基本导热机理。课题采用先通过分子动力学模拟研究气态物质在自由空间中的导热系数,再进一步考虑二氧化硅骨架结构,建立在有骨架结构存在时的气态物质导热模型,对两者分别通过分子动力学模拟研究计算导热系数,通过对比,对气凝胶的导热机理有更为深入的认识。
- 分子动力学模拟方法简介
分子动力学模拟(molecular dynamic simulation)计算,简称MD。该方法主要是依靠牛顿力学来模拟分子体系的运动,通过求解由相互作用的各个粒子的运动方程,得到每个粒子的空间位置、运动状态随时间的变化。结合粒子运动的基本描述和统计热力学的相关内容,得到物质的宏观行为特性。即为通过系统的微观细节得到工程中的宏观参数。
Alder和Wainwright[[15]]于1957年首次在硬球模型下,运用分子动力学研究物质的运动方程,开创了运用分子动力学模拟方法研究物质宏观性质的先例。随后,计算机技术的快速发展,MD技术也不断完善和发展。加上之后多体势函数的提出与发展,为分子动力学注入了新的活力。时至今日,MD的运用近六十年,由于分子动力学模拟可以得到许多实际实验中无法捕获的微观细节,分子动力学模拟在计算物理、化学、材料已被广泛应用,是比较成熟的研究手段。
- 分子动力学模拟的基本步骤[[16]]
- 确定研究对象
进行分子动力学模拟第一步要确定研究对象。研究的目的不同会采取不同的系综,如正则系综、为正则系综,等温等焓系综。在模拟环境中,如果体系粒子数、体积和温度保持不变,便是经常用到的正则系综。若粒子数,压力和温度保持不变,可以采取等温等压系综。若对于体系粒子数变化,可以采用巨正则系综。
- 确定分子的初始位置和速度
执行分子动力学计算必须要选取适当的初始条件,如起始位置、速度、执行温度和步长等。若初始条件选择不当,则往往需要浪费相当长的计算时间才能到达系统的热平衡,或者没有办法平衡。分子初始位置最好与实际情况类似,简单的分布有、简立方晶格分布、金刚石晶体分布和体心立方晶格分布。当模拟平衡后,得到的分子速度满足麦克斯韦统计速度分布。
- 确定势能模型
势能模型表现的是对于粒子的约束条件,模拟的精准度和势能模型的建立密切相关。因此,势能模型的建立是模拟的最重要的一个环节。由于研究对象的多样性,其微观结构十分多变且复杂,分子间的相互作用模型也不完全相同。对于简单分子,简单的有硬球、软球、(LJ)势、Born-Lande势、Morse势等。对于多体作用势有如:Stillinger-Weber作用势、Tersoff势。
描述含有N个原子作用的普遍作用势包括有单体、两体和多体,形式如(1-1)式:
(1-1)
此处代表第i个原子的位置,代表了N体作用势。当N增大,随着N的增大而趋向为零。一阶势能项用来描述固壁情况或者外加作用力。第二项描述两个粒子间的相互作用。
最常见的两体作用势是LJ作用势:
(1-2)
其中为粒子间的间距,为LJ势陷阱,为LJ平衡常数。LJ作用势是短距离作用关系,它经常用来描述液体或气体间的相互作用。
- 分子运动方程的建立
分子动力学方法的重点是对物理系统确定的微观表征。可以通过哈密顿描述和拉格朗日描述,也可以通过牛顿运动方程描述。每一种描述都会匹配一种运动方程,具体形式有分子间相互作用势决定。MD方法的具体过程就是通过分子运动方程求解数值解。通过离散替代连续,通过差分替代微分,建立一个有限差分格式,求解,从而在相空间中生成一条路径,沿这条路径的参数可以得到所需的各种理化参数。
以牛顿方程作为例子说明,原子的受力和运动关系如下:
(1-3)
上面对于速度和位移的计算运用了速度verlet。此方法编程简单,而且需要的存储空间小,所以目前的模拟程序,基本都是运用此算法实现。
- 边界条件
因为研究分子原子是很小的一部分,所以选择合适的边界条件可以大大减小模拟误差。常用的边界条件有:周期性边界条件、对称边界条件和固壁边界条件。
在模拟计算中,为了使得计算中系统的密度保持不变,常常采用周期性边界条件。周期性边界条件就是使自定义的元胞在自定义的空间中周期性重复排列,如图(a)显示二维盒中系统粒子的排列及移动方向,即:当计算系统中任一粒子移出盒外,则必有一粒子由相对的方向移入。这样可以使得模拟系统中的粒子数始终保持不变。
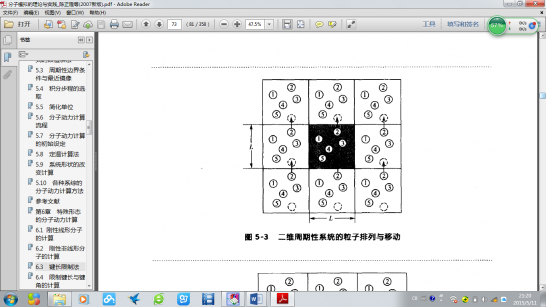
图1-1 二维模拟盒
这样,粒子的坐标可以表示为晶胞边长的倍数加上象粒子坐标,这样是可以得到无限大的体系。不过周期性元胞不能得到波长大于原胞长度的波动。
- 作用势的截断距离(cutoff distance)
小于模拟盒子的边长的一半以避免与同一粒子两个镜像同时作用。有简单截断,截断平移,最小镜像法三种处理方法。
- 特征长度(characteristic length)
某一特定物理量在空间的相关性的长度。原则上,模拟盒子的边长应该大于所关心的物理量的特征长度。具体操作上,可以通过变化模拟尺寸来了了解有限尺度效应的影响。
- 邻居列表(neighbor list)
每两个粒子都记算距离的遍历复杂度是O(N的平方),而实际上因为短程力可以做截断,大量远距离的力为零。除此,为了加快计算速度,把空间划分成立方块,每个立方块的边长为截断距离。计算粒子间距离时,对于给定粒子最临近的27个立方块(包括自身所在的立方块)内的粒子。计算复杂度降为O(N)。
- 导热系数的分子动力学模拟方法
近几年,器件尺寸的不断微小化推动了微电子、光电子技术和纳米技术。但同时,由于尺度效应,对传统的传热科学提出了新的挑战。在微纳米尺度下的传热问题,也是现今的重要课题。由于研究对象的尺度特殊性,传热问题也需要从原子和分子层面入手解决问题。同时,微纳米尺度实验的要求高,进行困难,加之计算机科学的不断发展,采用模拟方式是非常好的一种选择。综上,对于微纳尺度下的热传导问题,通过分子动力学模拟进行研究是有效和有前景的方法。
导热系数是材料的重要参数,通过对纳米材料的导热系数的分子动力学模拟研究,可以更加深入的理解纳米材料的导热机理同时也为对微尺度传热流体流动的研究提供基础帮助。
- 平衡态分子动力学模拟方法
平衡分子动力学模拟的概念是完全基于通过平衡状态计算物质导热系数而来的。在热科学还未引进分子动力学模拟的时候,分子动力学模拟已经可以得到经典粒子的输运特性,结合热导率的计算公式得到了最基本的算法。
剩余内容已隐藏,请支付后下载全文,论文总字数:23785字
相关图片展示:


该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


