论文总字数:12374字
目 录
1 引言 1
2 MGM(1,m)模型 2
2.1 MGM(1,m)模型的提出和构建 2
2.2 离散多变量MGM(1,m)模型 4
3基于线性时变参数的离散MGM(1,2)模型5
3.1 线性时变参数的离散MGM(1,2)模型的构建5
3.2 线性时变参数的离散MGM(1,2)模型系数矩阵的确定 6
3.3 线性时变参数的离散MGM(1,2)模型的推导及其求解 8
3.4 数乘变换下模型的参数特征 9
3.5 线性时变参数的离散MGM(1,2)模型的误差分析10
4 应用实例 11
4.1 实例背景11
4.2 数据收集、处理及参数求解12
4.3 模型预测13
4.4 模型的误差求解15
5 结论17
参考文献17
致谢18
基于线性时变参数的离散MGM(1,2)模型的构建
杜禹
,China
Abstract:Based on the analysis of GM (1, 1) model, this paper analyzes the original form of the modeling mechanism of MGM (1, m) model,and study a class of discrete multivariate MGM (1, m) model,and then have a further expanding and deepening. This paper added the linear time-varying parameters, and then calculate the parameters of the model by solving linear equations,which effectively avoid the error brought by the albino equations and the differential equations. Finally, this paper study data through analyzing actual examples for the construction of the model, and forecast the future data, then make a suggestion according to the conclusion.
Key words:Grey system theory;Multivariable grey model;Time-varying parameters;Forecast
1 引言
现代科学技术正在不断地飞速发展,无论是在现今的经济活动、科学教研活动还是人类的社会活动中,信息技术的交流都在扮演着越来越重要的角色。于是人们开始普遍重视信息的筛选、提取以及相应的处理方法,在这样的背景形式下,灰色系统理论应运而生。1982年,邓聚龙教授发表的《灰色系统的控制问题》,为其第一篇灰色系统论文,这标志着灰色系统理论的创立,作为新创建的一门理论,这是科学发展史上的一个飞跃。灰色系统是指内部信息不完全已知,其中部分信息已知,部分信息未知的系统。灰色系统的基本特点为:整体化、优化与模型化。灰色系统的研究对象是信息不完整、不确定的系统,其主要通过在经过处理的部分已知信息的基础上,提取那些有价值的信息,从而有效监控系统内部的运行情况以及对系统的演化规律进行正确的描述。在现实的生产实践活动中,由于普遍存在这种信息不完整、不明确的情况,使得灰色系统理论有着十分广泛的应用领域和发展前景。
灰色系统预测法是通过对原始数据序列进行适当的处理,根据数据显示出的特性选取构建适合的灰色模型,并且通过模型发现、挖掘、掌握系统中的转变及演化规律,并作出相应预测。灰色过程是指在一定方位内变化,并且与时间相关的过程,灰色过程中包含已知信息,同时也包含未知信息,灰色系统预测正是对这类过程的预测。虽然预测结果有时是随机的,或者数据显示杂乱无章,但是其仍然有序有界,这表明数据集合拥有其潜在的发展规律,而灰色预测正是运用这种规律,同时根据数据的特性来构建相应的灰色模型并且对灰色系统的发展作出预测。
在灰色系统领域中,GM(1,1)模型最先发展及应用,是灰色系统模型的基础与核心,根据其发展衍生出的许多灰色预测模型广泛应用于生产生活的各个领域。 GM(1,1)模型主要是针对复杂系统中某一个主导因素特征值的拟合以及相应的预测,从而能够揭示主导因素的演化规律以及其未来的发展变化趋势。但是,在实际应用中发现,GM(1,1)模型的拟合或预测效果有时好,有时又会出现较大的偏差,甚至有时候会完全失去效用。仔细分析GM(1,1)模型的建模原理,可以发现,从本质上讲其为一种指数预测模型,因此被预测对象自身的递变规律以及选用的数据序列的光滑程度等因素会影响到模型的预测精度,并且不能够保证构建的灰色系统模型的系统误差是可以忽略不记的,所以想要对数据序列进行较为精准的模拟和预测,GM(1,1)模型在这方面仍然有一定的欠缺。因而便有了GM(1,n)模型的推广,然而GM(1,n)模型又只能反映系统内部特征序列之间的变化规律,并不能用来进行系统预测,由此便有了多变量灰色模型的产生以及发展。早在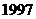 年,翟军等人[1]提出了多变量灰色模型,是从微分方程的角度构建模型并根据实例进行预测,是本文模型构建的基础。和本课题相关的国内文献中,杨保华[2]提出了将固定的参数转化为时变函数,从而与传统的灰色
年,翟军等人[1]提出了多变量灰色模型,是从微分方程的角度构建模型并根据实例进行预测,是本文模型构建的基础。和本课题相关的国内文献中,杨保华[2]提出了将固定的参数转化为时变函数,从而与传统的灰色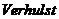 模型区分开,体现了新模型在提高灰色模型的预测精度上的优势,也给本文在参数的创新上一定的启发。张可等[3]在文中模型的构建给本文以思考。罗党等 [5]在文中提出一类离散多变量MGM(1,m)模型,从离散形式的角度构建模型,并根据实例数据进行预测优化,给本文以引导。熊萍萍等[7]在文中通过对原始数据的数乘变换,并进行相应的理论推导,来探讨多变量模型的性质及参数特征。熊萍萍等[8]在非等间距的情况下对多变量进行建模,并且提高了模拟预测精度,其思想和建模机理有广泛的应用价值和现实意义。
模型区分开,体现了新模型在提高灰色模型的预测精度上的优势,也给本文在参数的创新上一定的启发。张可等[3]在文中模型的构建给本文以思考。罗党等 [5]在文中提出一类离散多变量MGM(1,m)模型,从离散形式的角度构建模型,并根据实例数据进行预测优化,给本文以引导。熊萍萍等[7]在文中通过对原始数据的数乘变换,并进行相应的理论推导,来探讨多变量模型的性质及参数特征。熊萍萍等[8]在非等间距的情况下对多变量进行建模,并且提高了模拟预测精度,其思想和建模机理有广泛的应用价值和现实意义。
本文研究的主要内容为二元多变量灰色模型——MGM(1,2)模型,是单一变量的GM(1,1)模型在多元变量下的一种推广,将选择好的数据做完适当处理之后,本文致力于对选择的人均生活能源消费数据构建线性时变参数的离散MGM(1,2)模型,文章通过引入线性时变参数,从而构造出时变参数的多变量灰色模型。进一步研究模型性质,并接着对构建的模型进行误差分析检验。结果显示,本文模型能够较为准确地对序列数据进行模拟预测,能给生产生活提供一定的参考价值。
2 MGM(1,m)模型
2.1 MGM(1,m)模型的提出和构建
现实生产生活中,经济系统中的变量数量较多,各个变量之间相互关联、相互影响、共同发展,而且每一变量的变化发展并不是孤立的,一个变量会受到其他变量变化发展的影响,同时也在影响着其他的变量发展走向。针对这一点特性,翟军、盛建明、冯英浚等人提出了MGM(1,m)模型,即多变量灰色模型,它旨在从系统的角度对各个变量进行统一的描述,这考虑了上述变量的特性,更能适应实际生产和生活。
设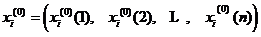 为原始数据序列,其一次累加序列为
为原始数据序列,其一次累加序列为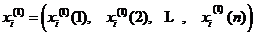 ,即
,即
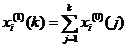
其中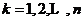
在利用数据序列来构建数学模型时,常常需要收集数据,然而因为一些特殊情况或者其他方面的困难,导致收集的数据序列并不完整,会出现部分空缺。当然,有的数据序列数据量是完整的,但是某些系统行为导致在某些时间节点上出现一些异常数据,这将会给进一步的研究工作带来许多麻烦,而若将异常数据剔除,又会产生数据空缺。因此,既要剔除异常数据,又要使得序列没有空缺,便需要使用构造新数据并且生成新序列的方法。
在灰色系统建模时,在一阶累加生成序列的基础上使用紧邻均值算法,从而减小数据序列的误差。记紧邻均值生成序列为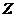 ,序列
,序列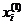 的紧邻均值生成序列为:
的紧邻均值生成序列为:
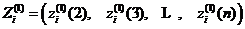
其中
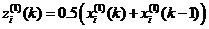
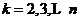
MGM(1,m)模型可以写成以下微分形式:
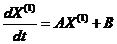 (1)
(1)
其中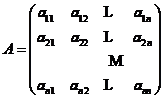 ,
, 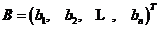
上式的连续时间响应式为:
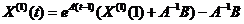 (2)
(2)
式(1)的离散化形式为:
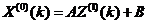
其中
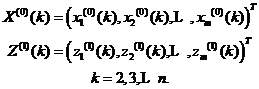
记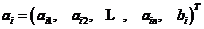 ,
,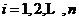 ,由最小二乘法得
,由最小二乘法得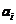 的辨识值
的辨识值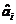 :
:
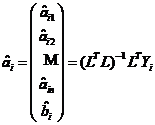
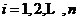 (3)
(3)
剩余内容已隐藏,请支付后下载全文,论文总字数:12374字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


