论文总字数：10597字

目录

一、引言 1

二、基本概念和方法 1

(一)贝叶斯思想 1

(二)LASSO算法 2

(三)EM算法 3

三、E步变量筛选算法 3

四、实例分析 5

五、讨论 9

六、结束语 10

参考文献 11

致谢 12

基于贝叶斯思想的变量筛选

冯泽洳

，China

Abstract:Implementation of high-dimensional data from the extraction of important information, data analysis is often encountered problems. Based on the Bayesian idea, this paper proposes the E-step variable selection algorithm, which can be used to estimate the posterior distribution by E-step iteration, so as to realize the variable selection of high-dimensional data under the linear model. The E-step variable selection algorithm is applied to select variables that affect Boston house prices, choosing the most variable for Boston's house prices: the DIS-weighted distance with the five Boston employment centers and the lower status of the population. By comparing the variables selected by the E-step variable selection algorithm with the variables selected by the LASSO algorithm, the fitting superiority of the E-step variable selection algorithm is 90%, while the LASSO algorithm has a good fit of 85% The E step variable screening is superior to LASSO algorithm.

Key words: Bayesian variable selection；the E-step variable selection algorithm；EM algorithm；LASSO algorithm

一、引言

在贝叶斯公式中，通过已知数据中的先验信息来求得后验分布。先验分布是基于经验和历史资料获得的，但是由于人为的误差和时间变化，先验分布可能会与实际数据中的信息不一致。为了获得与实际数据较为精准的信息，通过贝叶斯公式的计算，能够得到数据的后验分布。后验分布能够反映数据中的实际信息。在E步变量筛选算法中，运用贝叶斯思想，基于线性回归模型，依据回归系数的先验分布，通过E步算法迭代求得变量的后验分布，根据后验分布来观察变量的筛选情况。

本文运用贝叶斯理论的算法中进行学习讨论和实现，从中汲取和深化相关知识，借助EM算法^[1]，提出了对于变量筛选的算法：E步变量筛选算法。通过E步不断的进行抽样迭代，最终来得到变量的后验分布，观察后验分布来选取相关有效变量。

在E步变量筛选算法中，从高维数据中筛选出的变量为“最佳”数集。系数的先验分布是相互独立的，并且假定其为一个混合二元正态分布。而其正态分布的中心为0，对于协方差有两种情况：有一个分布的协方差很小，这时的分布是不被选入“最佳”数集变量系数的先验分布。而除此之外，其他的被选入“最佳”数集的变量系数的先验分布有较大的协方差。这一假定能够节省计算量和达到所要求的对高维数据进行降维，从而能够达到变量筛选。

E步变量筛选算法假定了回归系数的先验分布都是正态分布，在此基础上，E步通过系数的先验分布，利用詹森不等式和对数函数的凹性推导出了变量的后验分布，变量时，变量从数据中筛选出来；时，变量则没被筛选出来。由于变量与系数相关，因此从变量的后验分布中可以观察到高维数据的筛选情况，来达到降维目的。这一算法避免了其他的计算后验概率的繁杂过程以及收敛速度慢的不足之处，是个能够快速求得后验分布的算法。最大的优点是快速稳定和简单，在具体实现上简单易行，结果很直观，能够快速的从中选择出需要的变量的后验分布，实现了高维数据的变量筛选。

LASSO算法实际上也是贝叶斯算法。它是一种压缩估计，通过构造一个惩罚函数得到一个相对精简的模型，从而压缩了一些系数和一些系数为零，保留了子集收缩的优点。惩罚函数越大筛选出来的变量越少。这是一种可处理复共线性数据的有偏估计。LASSO算法不仅拥有模型的作用，还能够发挥贝叶斯统计的优点。LASSO算法避免了在高维数据的条件下，最小二乘法的不稳定性，将不显著的参数系数自动估计为0，从而得到筛选变量，实现降维目的。

二、基本概念和方法

(一)贝叶斯思想

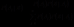(1)

式为贝叶斯公式，在试验没有进行之前，事件发生的概率为，称为先验概率或者经验分布。在试验进行之后，得到新的信息，即的新的信息。与此同时，通过贝叶斯公式可以计算出条件概率，而就是已知事件发生的情况下事件后验概率。总的来说，贝叶斯思想就是一个“由果导因”，经验分布推出后验分布的过程。

在对高维数据进行降维，筛选变量过程中，运用了贝叶斯思想，依据数据中的先验信息

求得后验概率，从获得的后验分布来筛选数据中重要变量，得到的数集就是“最佳”数集。

(二)LASSO算法

Tibshirani在1996年提出了LASSO算法。这种算法构造一个惩罚函数从而来获得一个精炼的模型；通过最终确定一些指标的系数为零，LASSO算法实现了指标集合精简的目的。该算法是一种处理具有复共线性数据的有偏估计。并且Tibshirani还提出：在我们假定回归系数的分布服从独立的双指数分布时，在本质上，LASSO的估计可以认为是一种贝叶斯后验的众数估计。LASSO的基本思想起源于线性回归，是在回归系数的绝对值之和小于一个常数的约束条件下，使得残差平方和最小化，从而能够产生某些严格等于0的回归系数，得到解释力较强的模型。根据模型改进的需要，数据挖掘工作者可以借助于LASSO算法，利用AIC准则和BIC准则精炼简化统计模型的变量集合，达到降维的目的。因此，LASSO算法是可以应用到高维数据的变量筛选中的实用算法。LASSO算法避免了在高维数据的条件下，最小二乘法的不稳定性，将不显著的参数系数自动估计为0，从而得到筛选变量和进行模型选择。

在线性回归中，通过最小二乘法来对数据进行拟合求解，但是在这一过程中，最小二乘既没有考虑到参数的先验信息，又没有考虑到根据实际的情况对参数进行限制，因此LASSO在最小二乘的基础上增加了约束形式，使得在对参数的估计上进行了一定的修正，不仅解决变量选择问题，还能够压缩回归系数。

LASSO算法主要的目的：。其中是惩罚参数。假设有数据是自变量，是因变量。在一般回归建立过程中，我们假定观测值独立或者关于给出的独立，假设是已标准化的，即。令，则用LASSO预测的结果：，并服从，这里是个可调参数。对于所有的，对的预测就是，不失一般性的假定，从而舍弃。