论文总字数:29914字
摘 要
我们研究了通过掺杂3d过渡金属原子的方法来在Bi2Te3, Sb2Te3三维拓扑绝缘体中建立铁磁性的可能性。通过基于第一性原理的密度泛函理论计算,我们研究了掺杂过渡金属原子在Bi2Te3和Sb2Te3中的分布情况,以及掺杂材料的能带结构和磁性。我们的结果显示,对于在Bi2Te3中单个掺杂的Co原子从能量上来看处于层内空隙位置比层间间隙掺杂位置更稳定,而对于Cr原子和Cu原子,分别处于Sb2Te3和Bi2Te3的层间间隙掺杂位置更稳定。进一步详细研究表明,当有多个3d金属原子插入层状三维拓扑绝缘体时,Co原子倾向于在Bi2Te3层间形成团簇结构,而Cu形成团簇的概率和均匀掺杂的概率相近,Cr倾向于在Sb2Te3中均匀掺杂。同时我们还发现Co原子掺杂的Bi2Te3显示了稳定的铁磁耦合,而且在外应力作用下,这种铁磁性变得更加稳定。而Cr掺杂的Sb2Te3则显示出了弱的反铁磁耦合。电子结构分析显示Co原子掺杂后的块体材料仍然是绝缘的,但是本征带隙减小。
关键词:拓扑绝缘体,掺杂,磁性,密度泛函理论
TAILORING MAGNETIC DOPING IN THE
THREE-DIMENSIONAL TOPOLGICAL INSULATORS
Abstract
We theoretically investigate the possibility of establishing ferromagnetism in the topological insulator Bi2Te3,Sb2Te3 via magnetic doping of 3d transition metal elements. The charge states, band structures, and magnetic properties of doped Bi2Te3, Sb2Te3 are studied using first-principles calculations within density functional theory. Our results show that Co prefer to form clusters in Bi2Te3 and Cr prefer to distribute uniformity. Electronic structure analysis reveals that Co doped materials are still insulating in the bulk but the intrinsic band gap of Bi2Te3 is substantially reduced. The calculated magnetic coupling suggests that Co doped Bi2Te3 is possible to be both ferromagnetic and insulating, while Cr doped Sb2Te3 tends to be weakly antiferromagnetic.
KEY WORDS: topological insulator, dope, magnetic properties, density functional theory
目 录
摘要 ……………………………………………………………………………………Ⅰ
Abstract ………………………………………………………………………………Ⅱ
- 绪论 ………………………………………………………………………1
1.1 引言 ………………………………………………………………………1
1.2 量子霍尔效应与拓扑绝缘体 ………………………………………………1
1.2.1量子霍尔效应与量子自旋霍尔效应…………………………………1
1.2.2拓扑绝缘体…… ………………………………………………………2
1.3量子反常霍尔效应 …………………………………………………………3
1.4磁性掺杂拓扑绝缘体 ………………………………………………………4
参考文献 ……………………………………………………………………5
- 理论基础和计算方法 ………………………………………………………6
2.1 引言 ………………………………………………………………………6
2.2 第一性原理 ………………………………………………………………6
2.3 Hartree-Fock近似 ……………………………………………………………6
2.4密度泛函理论 ………………………………………………………………7
2.4.1 Hohenberg-Kohn定理 …………………………………………………7
2.4.2 Kohn-Sham方程 ………………………………………………………8
2.4.3 LDA 近似………………………………………………………………8
2.4.4 GGA 近似………………………………………………………………9
2.5 Bloch定理 …………………………………………………………………10
2.6赝势 …………………………………………………………………………11
2.7本论文所用的软件 …………………………………………………………12
2.7.1 VASP ……………………………………………………………………12
2.7.2 VASP的主要输入文件…………………………………………………13
2.7.2 VASP的主要输出文件…………………………………………………13
参考文献 ……………………………………………………………………14
第三章 过渡金属掺杂三维拓扑绝缘体 ……………………………………………15
3.1 引言 ………………………………………………………………………15
3.2 模型和方法 …………………………………………………………………16 3.3 结果和讨论 …………………………………………………………………17
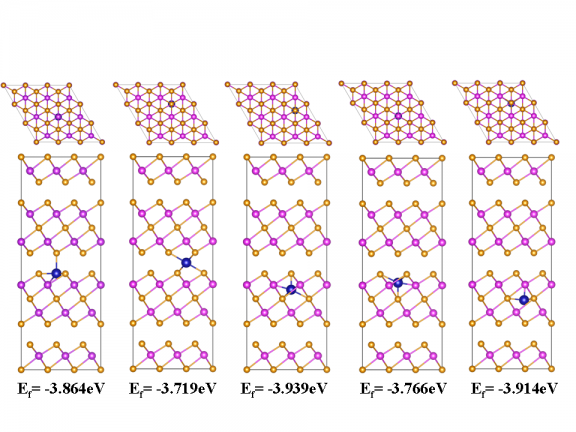
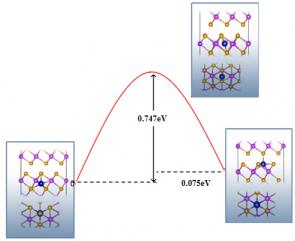
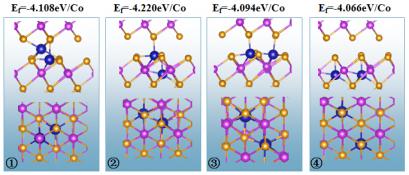
3.3.1 Co修饰下的Bi2Te3晶体结构和动力学特征 ………………………17
3.3.2 Cu修饰下的Bi2Te3晶体结构和动力学特征 ………………………19
3.3.3 Cr修饰下的Sb2Te3晶体结构和动力学特征 ………………………20
3.3.4 Co、Cr修饰下的Bi2Te3和Sb2Te3晶体的磁性与应力作用的影响…21
3.3.5 Co修饰下的Bi2Te3晶体的能带结构 ………………………………22
3.4总结……………………………………………………………………………22
参考文献 ……………………………………………………………………22
第四章 总结和展望 …………………………………………………………………24
致谢 ……………………………………………………………………………………25
第一章 绪 论
1.1 引言
在传统意义上固体材料可以按照其导电性质分为导体和绝缘体,而拓扑绝缘体是介于导体和绝缘体两者之间的一种新的宏观量子物态。拓扑绝缘体材料的内部是有能隙的绝缘态,但表面或边界是没有能隙的金属态,并且时间反演对称性保护着材料表面或边界的金属性 [1-2]。随着人们研究的推进,从二维结构的(Hg,Cd)Te量子阱到三维结构的Bi1-xSbx,Bi2Te3,Bi2Se3,Sb2Te3,Bi2Te2Se等[2-5],拓扑绝缘体材料家族的成员在不断增加。
理论预言,可能在被引入磁性杂质的拓扑绝缘体材料中发现一些奇特的物理效应以及预言中的粒子[6-8],例如通过拓扑绝缘体和常规超导体的近邻效应,有可能生成Majorana费米子[8]。由于拓扑绝缘体磁性材料的众多独特性质,在过去的几年中掀起了巨大的研究热潮。这一章主要介绍和拓扑绝缘相关的物理效应以及我们主要研究的磁性原子掺杂拓扑绝缘体。
1.2 量子霍尔效应与拓扑绝缘体
1.2.1 量子霍尔效应与量子自旋霍尔效应
整数量子霍尔效应(IQHE)于1980年被Klitzing等人发现,当时他们正在低温环境下测量二维半导体的霍尔电组[9]。他们在测量过程中发现,二维半导体的霍尔电导随着磁场的增强总是在直线上升趋势中出现一系列平台,并且总是整数倍变化,表现出量子化。在这之后的1982年,人们发现了分数量子霍尔效应(FQHE)[10],在更强磁场和更低温度条件下测量AlGaAs/GaAs异质结中的二维电子气的霍尔效应的实验中,霍尔电导出现了分数倍变化。整数量子霍尔效应和分数量子霍尔效应统称为量子霍尔效应(QHE)。量子霍尔效应产生的物理机制是,在外加磁场的作用下,体系内部产生了朗道能级,有的能级被电子占据而有的并没有被占据,于是在没有被占据和被占据了的能级之间出现了能隙,这和传统意义上的绝缘体的能隙非常相似。虽然体系内部是绝缘的,但是载流子仍然在样品边缘的通道中传导(图 1.1(a)),构成特殊的边缘态,从而在同一体系中出现了体态和边缘态两种状态,形成量子霍尔效应。在量子霍尔效应发现之前,人们总是认为某种对称性的破缺导致物质量子态的出现,量子霍尔效应的出现打破了这种观点,因为在量子霍尔效应体系中,对称性并没有破缺,波函数的拓扑性质对应了特殊的量子态。
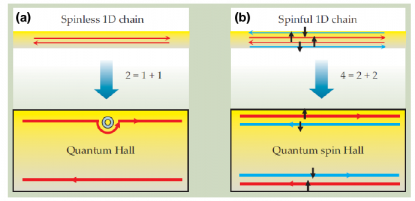
图 1.1(a) 量子霍尔效应的边缘态;(b) 量子自旋霍尔效应的边缘态,两支边缘态自旋方向不同。
在量子霍尔效应的基础上,我们将电子的自旋考虑进来,就可以得到量子自旋霍尔效应。量子自旋霍尔效应的物理图像如图 1.1 (b) 所示。和霍尔效应一样,量子自旋霍尔效应中电子在边界上传导,但在霍尔效应中,在某一边界上电子只沿着一个方向传导,而在量子霍尔效应中,每一个边界上有两条边界态构成的带,两个边界态对应的电子自旋是相反的,因此电子可以沿着两个相反的方向传导,但两个方向上的电子数目相同,没有净电流,没有霍尔电导,然而有一个净自旋流,并且它也是量子化的,因此称为量子自旋霍尔效应。在2005年,Pennsylvania 大学的 Kane C. J. 和 Mele E. J. 教授首次提出在单层石墨烯中可能存在量子自旋霍尔效应 [11] ,但是中国科学院物理研究所的姚裕贵研究员等随后的工作表明单层石墨烯中很难观察到量子自旋霍尔效应,因为虽然自旋轨道耦合在石墨烯中打开了能隙,但其仅为μeV量级,大小可忽略不计,因此将很难在实验上观测到[12]。很快Stanford大学的张首晟研究组在理论上预言在HgTe/CdTe 量子阱体系中能够实现量子自旋霍尔效应[13],之后不久该预言就被德国的Laurens Molenkamp研究组在实验上证实[14]。在量子自旋霍尔体系中,由于强的自旋轨道耦合作用,载流子沿着边缘无耗散地传输,因此有希望应用于下一代自旋电子学器件。
1.2.2 拓扑绝缘体
通常来说,广义上的拓扑绝缘体包含两种拓扑量子态,一种是系统不受到时间反演对称性保护,另一种是系统受到时间反演对称性保护。以二维体系为例,第一种是量子霍尔态,它的时间反演对称性由于磁场作用而破缺,这种非平庸的拓扑态能够和量子霍尔电导直接联系起来。第二种是量子自旋霍尔态,本质上由体系内强烈的自旋轨道耦合引起,并受到时间反演对称性的保护。拓扑绝缘体的共同的特点是在其内部不存在载流子的运动,表现出绝缘性,但在其边缘却有载流子传输,图 1.2(a)是第二种二维拓扑绝缘体的能带结构。在体能隙之间有两支边缘态,它们具有不同的自旋取向,在 k=0 处它们相交于一点,在交点附近,能量-动量的色散关系是线性的(即 E∝ k)。
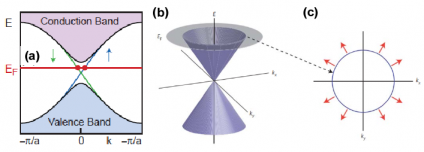
图 1.2 (a) 二维拓扑绝缘体的能带结构 (b) 三维拓扑绝缘体的表面态。
二维拓扑绝缘体的边缘态是一维的,可调控的自由度有限。三维拓扑绝缘体的边缘态是二维的,就便于可调控的自由就增多。2007 年,Pennsylvania 大学的 Kane C. J. 和 Mele E. J.教授将量子自旋霍尔态的概念由二维扩展到三维,从而在理论上预言了一种新的拓扑绝缘态,称作为强拓扑绝缘体 [15] 。至此,拓扑绝缘体的研究领域被大大拓宽。对于三维拓扑绝缘体的二维的表面拓扑态,其不同方向的E-k关系曲线形成形成圆锥形状,称为狄拉克锥(Diraccone),如图1.2(b)所示。
剩余内容已隐藏,请支付后下载全文,论文总字数:29914字
相关图片展示:
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


