分层媒质结构中的电磁场散射计算

论文总字数：22268字

摘 要

在很多实际应用中，人们都需要计算分层媒质结构内的电磁场，比如地球探测，遥感以及微波/毫米波多层电路等。本文基于分层媒质空域并矢Green函数的精确、快速计算，利用积分方程矩量法，计算分层媒质表面有限周期阵列贴片的散射场。

若在分层媒质结构的表面附有一导体贴片阵列，则当有电磁波从上方空间入射时，表面贴片上将产生一定的电流分布。同时周围空间也将形成一定的散射场。为了能运用矩量法计算表面贴片的电流分布，将贴片进行三角形网格剖分，并用各小三角形面上的电流值来表示整个贴片上的电流分布。在矩量法的具体应用与计算中，选用定义在三角形面对上的RWG基函数。在阻抗矩阵的计算填充中，选用三角形面上的数值积分以避免Green函数的奇异性。当根据入射电磁场确定电压激励向量后，便可通过求解矩阵方程得出各RWG边元的电流系数，从而求出整个贴片上的电流分布并在MATLAB中绘制出电流分布图。简要介绍了由混合位积分方程推导得出平面分层媒质空域并矢Green函数的过程。并在此基础上根据贴片天线的远场与近场辐射算法，计算空间的辐射强度并绘制出分布图。同时，针对给定的贴片形状与排列形式的贴片阵列，以及在一定频率与介电常数的情况下的具体计算结果进行了讨论。

关键词：分层媒质，矩量法，并矢Green函数，混合位积分方程，RWG基函数，贴片天线

Abstract

In lots of practical applications, it is necessary to calculate the electromagnetic field within the multilayered structures. For example, earth detection, remote sensing, microwave/millimeter wave multilayered circuits, etc. Based on the accurate and fast computation methods of spatial domain dyadic Green’s function for multilayered structures, this dissertation concentrates on the calculation of the scattering field generated by a periodical patch array on the surface of multilayered structure, using method of moments of the mixed potential integral equation (MPIE-MoM).

If a patch array is attached to the surface of multilayered structure, there will be a certain current distribution on the patch when electromagnetic waves incident from above. Also, the scattering field will exist in the surrounding space. To calculate the current distribution on the surface patch by MoM, triangulate meshing is applied, and then represent the current distribution with the current value on each triangle. In the specific calculation of MoM, the RWG base function defined on a triangle pair is choosed. The numerical integral on triangle surface is used in the calculation of the impedance matrix, to avoid the singularity of Green’s function. After the determination of the voltage excitation vector, the current coeffients of each RWG edge element can be acquired by solving a matrix equation. Then we can have the current distribution on the whole patch and show the current map in MATLAB. The procedure of deducing the spatial domain dyadic Green’s function for multilayered structures by MPIE is also briefed. According to the far-field and near-field radiation algorithm of patch antenna, the radiation intensity is calculated along with the space distribution map. Meanwhile, as for certain shapes and certain arrangement form of the patch array, the specific results in the case of given frequency and dielectric constant are discussed.

KEY WORDS: multilayered structure, method of moments(MoM), dyadic Green’s function, mixed potential integral equation, RWG base function, patch antenna

目 录

摘 要 3

Abstract 4

第一章 绪 论 6

1.1 引言 6

1.2 分层媒质中电磁场散射的研究现状 6

1.3 本文的研究目的和主要研究内容 7

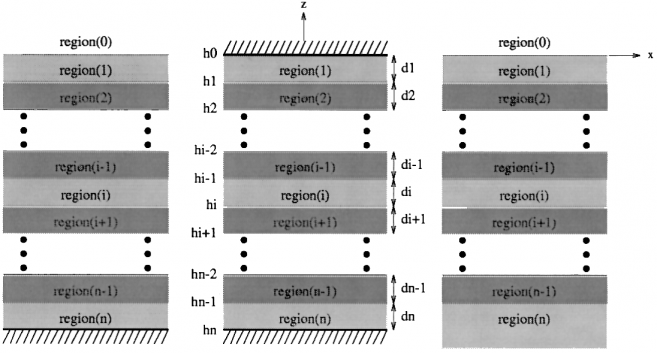
第二章 分层媒质结构中的矩量法数学模型 9

2.1 矩量法的数学原理 9

2.2 RWG基函数与表面贴片的三角网格剖分 10

2.3 阻抗矩阵及表面电流分布的计算 12

第三章 基于分层媒质并矢Green函数的辐射场计算 15

3.1 混合位积分方程 15

3.2 分层媒质的并矢Green函数 17

3.3 表面贴片辐射场的计算 20

第四章 数值算例与讨论 22

4.1 表面贴片电流分布 22

4.2 辐射场分布 24

致谢 27

参考文献 28

1. 绪 论
   1. 引言

在很多实际应用中，人们都需要计算分层媒质结构内的电磁场，比如地球探测，遥感以及微波/毫米波多层电路等。此外，大气层、地理岩层、海洋、热带雨林植被等真实环境都可以被抽象为多层媒质结构。而微波毫米波集成电路以及超大规模集成电路技术的快速发展，使得人们越来越多地关注分层电路的严格、精确、快速建模与仿真。计算机科学的飞速发展大大促进了信息技术领域中精确电磁仿真科技的发展。很多国防与民用研究都涉及到电磁建模与仿真，需要精确、快速、稳定的电磁仿真软件作为辅助设计工具。成熟可靠的电磁仿真系统，需要具备两种特性：准确建立环境与目标物体的物理模型，以及应用快速、精确、稳定的数学方法对该模型进行求解。

矩量法（MoM）以稳定、准确等特性被广泛应用于各种复杂电磁问题的数值计算，而分层媒质空域并矢Green函数及混合位积分方程是矩量法应用于分层媒质结构全波电磁仿真的关键。随着计算机技术日益发展，矩量法早已得到了高度关注，在计算电磁学领域中已经是一不可缺少的重要分支。而在对平面分层媒质的分析中，矩量法的应用常需要以混合位积分方程（MPIE）为基础的对分层媒质适用的空域并矢Green函数。若能快速准确地得出分层媒质的空域并矢Green函数，则矩量法的优势将能得到充分体现。

电磁波在分层介质结构中传播，会发生反射、透射、吸收以及能量转化等物理过程。如果分层介质表面的金属贴片单元以一定的周期阵列形式出现，则平面电磁波在透射过该结构后将汇聚于一点。即多层有限周期阵列结构可实现平面波的聚焦，这一结构被称为平面透镜。根据光路的可逆性，若在一平面透镜的焦点处有一点电磁波源（如喇叭天线），其产生的球面波经此结构透射后将形成平面波。这是实现平面电磁波的有效方法，并已被广泛应用。因此，对分层媒质结构中传播的电磁波的散射场进行快速、精准的计算，是决定其能否有效用于电磁仿真等实际应用的关键。本文基于分层媒质空域并矢Green函数的精确、快速计算，利用积分方程矩量法，计算分层有限周期阵列的散射场。

• 1. 分层媒质中电磁场散射的研究现状

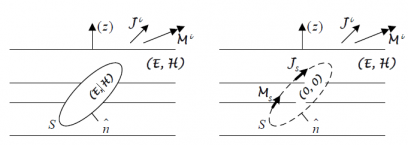
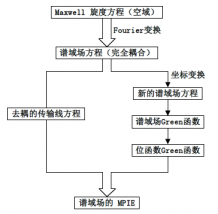
在对分层媒质中传播的电磁波进行分析时，Green函数具有显而易见的重要意义。从实质上来讲，Green函数是一线性系统对一点源激励的响应函数。Green函数在电磁场中一般以并矢形式出现，因此也称做电磁并矢Green函数。为对分层媒质结构中有限周期阵列的散射场进行精确的分析计算，需要精确、快速地得到平面分层媒质空域并矢Green函数。如果能够得到给定源的空域并矢Green函数，则可以求得其在空间任意处产生的电磁场。而在电磁场积分方程中，场量的Green函数往往具有高阶奇异性，这给问题求解带来了困难。相比于电场积分方程(EFIE)，混合位积分方程 (MPIE) 更适合分层媒质结构的建模分析。若借助标量位和矢量位来表示场，则可导出混合位积分方程，而关于位函数的Green函数的奇异性则相对容易处理^[1]。混合位积分方程在分层媒质中的优势在于，相比于场函数，位函数核中Sommerfeld型积分收敛更快，更易于快速计算。目前，已有很多文献详尽推导了多层（三层以上）媒质中的并矢Green函数。而在本文中，我们更关心如何将其运用于求解多层媒质中电磁波的散射场。

将谱域Green函数转化为空域，需要对其谱域表达式做Sommerfeld变换，即计算Sommerfeld型积分。鉴于被积函数是高振荡且衰减缓慢的，这一步骤非常耗时。曾有离散复镜像方法（DCIM）被提出来近似计算带有多个复指数项的被积函数，使计算非常有效。离散复镜像法可直接得到空域并矢Green函数而不需要计算数值积分。然而，应用DCIM之前必须确定以下参数：采样范围、展开项与表面波极点。前两个参数强烈依赖于层的属性，而超过三层的媒质的表面波极点很难找到^[2]。因此DCIM并不适用于三层以上的分层媒质。

在具体计算分层媒质中的电磁场分布时，需要对数学模型进行离散。本文中选用矩量法（MoM）将混合位积分方程转化为矩阵方程进行求解。离散方法除矩量法（对积分方程进行离散）外，还有有限元法（对Maxwell微分方程组的泛函变分形式进行离散）以及时域有限差分法（直接对Maxwell微分方程组进行离散）等。其中矩量法以稳定、准确等特性被广泛应用于各种复杂电磁问题的数值计算。不同于有限元法与时域有限差分法的是，基于Green函数的核心作用，矩量法只需要对分层媒质中的导体表面进行离散，而不需要剖分介质部分。将导体表面的未知电流分布展开为适当的局域基函数的线性组合，然后将积分方程转化为线性代数方程组。对线性代数方程组进行求解即可得到导体表面的电流分布。

矩量法的计算效率由其阻抗矩阵的填充技术直接决定。获得闭式空域并矢Green函数能够极大减少阻抗矩阵的填充时间，从而提高计算效率。而且现已有方法得出适合矩量法计算的空域并矢Green函数。目前，基于混合位积分方程的矩量法这一数学模型已成熟，且已具备基础的程序框架。以上核心算法已在简单模型上得到验证。现需要推广与扩展应用，并根据结果绘制贴片表面电流分布。在建立贴片天线三维远场辐射分布（天线方向图）的数学计算公式后，便可据此编写计算程序。此外，对于多层媒质结构，每一层的外加激励源（入射场）都不同，表面电流分布也不同，需要逐层推导计算。同时，该问题中阻抗矩阵的规模相当大，在实际编程计算时需要反复调试并对算法进行一定的优化。

• 1. 本文的研究目的和主要研究内容

本文以平面分层媒质的空域并矢Green函数及混合位积分方程矩量法为基础，对电磁波在分层介质中的散射场进行了计算分析。其中分层介质表面带有以有限周期阵列形式排列的金属贴片。主要内容如下：

1. 针对有限周期阵列结构的表面金属贴片，运用基于MPIE的矩量法模型，在MATLAB中建模分析，运行调试普通贴片天线的矩量法计算程序，计算得出贴片的表面电流分布并绘制分布图；
2. 针对分层介质（其中各层介电常数不同），在分层媒质的空域Green函数快速算法的基础上推导散射场分布，建立贴片天线的三维远场辐射分布（天线方向图）的数学计算公式，并根据表面贴片的电流分布计算辐射场；
3. 根据计算结果绘制场分布图，并针对给定的入射电磁波及介质的介电常数的情况对结果进行分析。

本文撰写安排如下：

在第二章中，首先介绍矩量法的数学原理与平面分层媒质结构中基于混合位积分方程的矩量法数学模型，包括矩量法中定义在三角面形对上的RWG基函数，表面贴片的三角网格剖分，以及阻抗矩阵的计算中对角线元素的奇异性处理；然后，针对从上方空间入射的平面波，得出电压激励向量并通过求解矩阵方程计算分层介质表面贴片的电流分布；

在第三章中，首先介绍由电磁场的混合位积分方程得出分层媒质的并矢Green函数的数学推导过程，其中包括不同形式偶极子激励，不同场-源相对位置对应的矢量位和标量位Green函数，并介绍了3层以上平面分层结构中不同场-源位置对应的谱域Green函数的计算；简要阐述了将谱域Green函数转化到空域的算法以及对Sommerfeld积分中被积函数奇异性的处理；并运用表面贴片天线辐射场的算法计算空间的辐射场强度；

剩余内容已隐藏，请支付后下载全文，论文总字数：22268字

相关图片展示：