论文总字数:6529字
目 录
1预备知识 3
1.1 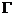 函数 3
函数 3
1.2 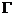 函数 4
函数 4
2狄利克雷公式与余元公式 5
2.1 狄利克雷公式 5
2.2 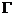 函数的余元公式 7
函数的余元公式 7
2.3 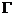 函数的余元公式 8
函数的余元公式 8
3应用解析 10
3.1 用于定积分计算 10
3.2 用于极限求解 14
参考文献 16
浅谈欧拉积分及其应用
胡可旺
,China
Abstract:In this paper, we talk about two kinds of parameter improper integral including the first kind of Euler integral Beta function and the second type Gamma function, which are widely applicated in many fields like mathematics, physics and so on. We mainly discuss some properties of the two types of Euler integral. As a supplement to the relevant content of the textbook, we deduce and demonstrate Dirichlet Formula and Odd Element Formula, which reveal the relation between the two kinds of Euler integral. Last, we elaborate some applications of Euler integral in calculating integrals and solving limits by giving examples.
Key words: Beta function; Gamma function; calculating integrals; solving limits
欧拉积分是瑞士数学家欧拉首先提出并研究的,包括以下两类含参量反常积分:第一型欧拉积分即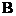 函数,第二型欧拉积分即
函数,第二型欧拉积分即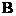 函数.欧拉积分应用广泛,不仅仅应用于数学的一些分支,例如概率论与数理统计、数理方程等学科,在物理学、工程学等众多领域中都有着积极的作用.作为在含参量积分基础上引进的非初等函数,欧拉积分可以帮助我们解决仅靠初等函数难以解决的问题.例如一些比较复杂的定积分计算问题,计算定积分的方法一般而言是先求出被积函数的原函数,然后再根据牛顿-莱布尼茨公式代入上下限进行计算,然而有许多定积分的原函数的计算过程非常繁琐,工作量庞大.但是通过作适当的变量代换将其转化为欧拉积分就可以轻松求解.再如一些含参量无穷积分趋于无穷时的极限问题,一般来说用常规方法去求解这类问题是非常困难的,甚至无从下手,然而合理地运用欧拉积分却可以轻松地将其解决.掌握欧拉积分的性质以及一些重要的结论,将会给我们对许多问题的研究带来很大的便利,这也是本文的目的所在.
函数.欧拉积分应用广泛,不仅仅应用于数学的一些分支,例如概率论与数理统计、数理方程等学科,在物理学、工程学等众多领域中都有着积极的作用.作为在含参量积分基础上引进的非初等函数,欧拉积分可以帮助我们解决仅靠初等函数难以解决的问题.例如一些比较复杂的定积分计算问题,计算定积分的方法一般而言是先求出被积函数的原函数,然后再根据牛顿-莱布尼茨公式代入上下限进行计算,然而有许多定积分的原函数的计算过程非常繁琐,工作量庞大.但是通过作适当的变量代换将其转化为欧拉积分就可以轻松求解.再如一些含参量无穷积分趋于无穷时的极限问题,一般来说用常规方法去求解这类问题是非常困难的,甚至无从下手,然而合理地运用欧拉积分却可以轻松地将其解决.掌握欧拉积分的性质以及一些重要的结论,将会给我们对许多问题的研究带来很大的便利,这也是本文的目的所在.
本文主要讨论欧拉积分的性质及其应用.在本文第1节,两类欧拉积分的基本定义以及连续性等基本性质都以预备知识的形式给出;作为教科书内容的补充,在本文第2节将着重讨论两类欧拉积分的余元公式以及沟通它们联系的狄利克雷公式;最后,在本文第3节将着重介绍欧拉积分在计算定积分和求解极限的一些具体应用.
1预备知识
本节介绍有关欧拉积分的一些基本知识.由于多数教科书都对这些基本知识进行了详细的介绍,所以对于两类欧拉积分的定义域及一些基本性质的证明,本文不再赘述.
1.1 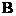 函数
函数
定义1[1] 由下式定义的含参量的瑕积分称为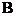 函数:
函数:
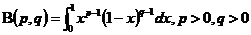 .
.
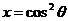 函数除了定义1中的形式外还有其他形式.例如令
函数除了定义1中的形式外还有其他形式.例如令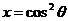 ,则有
,则有
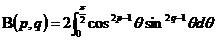 ; (1)
; (1)
令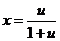 ,则有
,则有
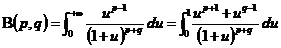 . (2)
. (2)
性质1 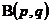 在定义域内连续且具有各阶连续偏导数,且有
在定义域内连续且具有各阶连续偏导数,且有
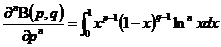 ,
,
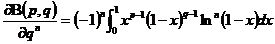 .
.
性质2(对称性) 对任意的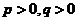 ,有
,有
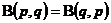 .
.
性质3(递推公式) 对任意的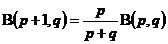 ,有
,有
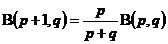 ;
;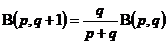 ;
;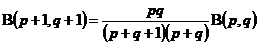 .
.
特别地,对任意正整数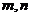 ,有
,有
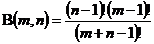 .
.
当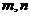 都取1时,有
都取1时,有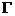 .
.
1.2 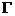 函数
函数
定义2[1] 由下式定义的含参量的无穷积分称为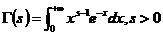 函数:
函数:
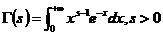 .
.
除了定义2中的形式之外,在应用中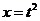 函数经常以其他形式出现,例如令
函数经常以其他形式出现,例如令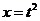 ,则有
,则有
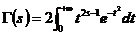 ; (3)
; (3)
令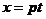 ,则有
,则有
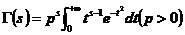 ; (4)
; (4)
令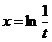 ,则有
,则有
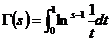 . (5)
. (5)
性质1 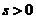 在定义域
在定义域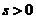 内连续且具有任意阶导数,且有
内连续且具有任意阶导数,且有
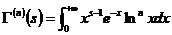 .
.
性质2(递推公式) 对任意的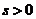 ,有
,有
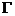 .
.
推论 利用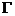 函数的递推公式我们还可以推导出如下结论:
函数的递推公式我们还可以推导出如下结论:
(1)对任意的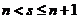 ,令
,令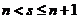 (
(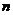 为自然数)有
为自然数)有
剩余内容已隐藏,请支付后下载全文,论文总字数:6529字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


