超几何级数恒等式与π的级数展开式

论文总字数：5293字

目 录

1引言 3

1.1 超几何级数简介 3

1.2 无理数的无穷级数展开 4

2 超几何方法与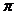的展开式 4

3结论 7

4讨论 8

参考文献 8

致谢 10

超几何级数恒等式与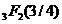的级数展开式

杨建龙

，China

Abstract：This article mainly expounds the applications of hypergeometric series into expansion for some important mathematical constants. By Gosper’s two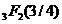-series summation formulae, two 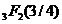-expansion formulae with free parameters are established．

Key words：generalized hypergeometric series；Gosper’s 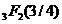-series sum; series expansion of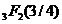

1引言

1.1 超几何级数简介

超几何级数属于特殊函数范畴，与组合数学密切相关，在数论、理论物理和计算机代数等领域具有广泛的应用．尤其对超几何级数恒等式的研究一直是组合学者和特殊函数学者感兴趣的课题．

定义１^[1,2] 关于参变量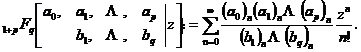的幂级数

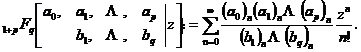
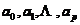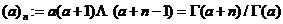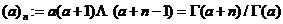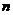称为超几何级数．其中和分别叫做该级数的分子参量和分母参量，称为的次升阶乘．

1655年，John Wallis在他的《Arithmetica Infinitorum》一书中第一次使用了“超几何的”(hypergeometric)术语，并且研究了如下级数：

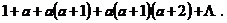
之后很多数学家研究了与之类似的级数，特别是Gauss在其著作中给出了含有三个参变量的Gauss级数的定义

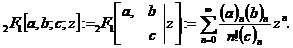
Euler对这上述级数的终止形式给出了下述著名关系式^[3]

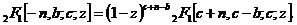
Vandermonde在1770年给出了二项式定理的推广形式

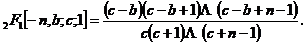
Gauss在1812年他的博士论文“Disquisitiones generales circa seriem infinitam”里，证明了著名的“Gauss求和定理”^[1]：

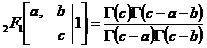，其中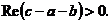

1836年，Kummer首次将“超几何”这一专业术语用于级数

，

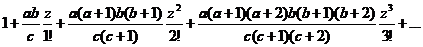并证明了Gauss函数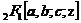是下列二阶微分方程的解

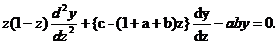
在这期间，许多数学家开始推广Gauss级数，也有很多方法去推广，比如增加参数的个数等等．慢慢的一般超几何级数的求和定理被数学家们给出．值得一提的是E.Heine用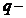模拟：

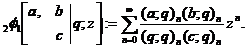
来推广Guass函数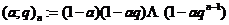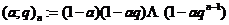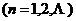，，，．这类级数称为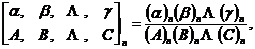-级数或基本超几何级数．

为表述方便，我们常用下列两个缩写形式来表述多个升阶乘和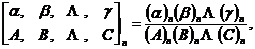-函数的分式形式

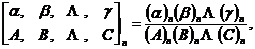
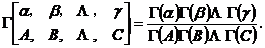
1.2 无理数的无穷级数展开

无理数是无限不循环小数，在实际应用中，我们往往只使用其近似值，从这个角度考虑，探索无理数的级数展开式具有重要意义．圆周率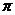是重要的的无理数之一，早在古老的埃及文物中，就有着对圆周率的记载．刚开始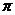并没有圆周率的意思，是英国数学家Jones首先将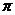作为符号来用．对于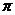的计算大致可以分为3个时代，第一是微积分出现之前的阶段，然后就是利用微积分计算的时代，最后就是现在计算机计算的时代．

大约在1400年，Sangamagrama发现了第一个关于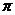的级数展开式：

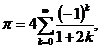
在17世纪Gregory和Leibniz又重新发现了这个展开式，此展开式因此被称为Gregory-Leibniz级数．1914年 Ramanujan举例写出了17个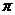的级数展开，随后，各种各样的方法被应用在这方面的研究上．比如利用超几何方法、差分算子理论、WZ方法、Eisenstein级数表示等等方法，Chu^[4,5]、Baruah-Berndt^[6]、Wei-Gong^[7]、Guillera^[8,9]、Liu^[10,11]等人推导出来一系列的与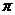和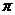有关的级数展开式．这些工作足以说明，与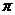相关的无理数展开式的研究越来越被重视．

2 超几何方法与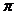的展开式

在本节中，我们来探讨超几何级数恒等式在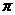的无穷级数展开方面的应用．首先我们要提到的是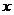函数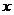，函数与超几何级数的恒等式是密切相关的．对于一个复数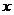，通过欧拉积分定义了函数

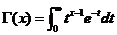, 其中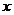

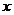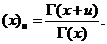对于两个复数和，存在

剩余内容已隐藏，请支付后下载全文，论文总字数：5293字