论文总字数:8617字
目 录
摘要 ················································1
引言·················································3
1概率论在不等式及积分上的应用··························3
1.1利用方差的非负性证明不等式·················· ········· ······3
1.2利用詹森不等式证明不等式·················· ········· ······· 4
1.3利用常见分布的数字特征求积分················ ········· ······ 7
1.4通过构造概率模型法计算积分················ ········· ········9
2概率论在极限上的应用············· ········· ··········· 9
2.1求解数列极限··········································· 9
2.2构建概率模型求无穷级数的和································ 10
3概率论在生活中的应用································· 12
3.1期望与方差的应用······································· 12
3.2伯努利概型的应用········································13
3.3贝叶斯公式的应用······································· 13
总结················································· 14
参考文献··············································14
浅谈概率论的应用
陶盈春
.
Abstract:Probability theory is an important branch of mathematics, which is a subject with a widerange of applications. Probability calculation and description can make people more clearly
understand and solve the problems. In this paper, probability theory penetrates to the
mathematical analysis, and solves inequalities in mathematical analysis, integral, limit, and
simplify solving process by using the knowledge of probability theory. The explanation of these
problems in the theory of probability is given, compared with the method of mathematical analysisto explain the convenience of probability theory. Moreover,it introduces the application of
probability theory in economic, markets, insurance and other fields briefly from the angle of
numbers, and illustrate the probability brings so much convenience to the human life.
Key words: Jansen’s inequality; probability model; probability integral; limit.
0引言
早期,人们普遍把概率中的理论与方法应用在人口统计和赌博等方面.而随着人类社会的高速发展,人类需要了解更多在不能确定的现象中所隐含的必然规律,并且运用数学的方法来研究出现既定结果的可能性,继而产生了概率论,并且使它逐渐发展成为一门具有广泛应用性的学科.概率论的研究方法正在逐步渗透到各领域,如生物科学,军事科学,自然科学等也体现了概率论的广泛应用性.本文将概率知识渗透到数学分析以及实际应用中,运用詹森不等式,林德贝格-勒维中心极限定理等概率论知识解决数学分析中不等式,积分以及极限等问题.利用数学分析法解决某些问题,解题过程较困难并且复杂,而运用概率论的方法不仅可以简化解题过程而且可使问题更加简单易懂.同时从数字的角度就概率论在实际生活中的应用进行了简单介绍,说明概率论的广泛应用性.
1概率论在不等式及积分上的应用
1.1利用方差的非负性证明不等式
性质1.1.1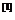
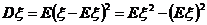 ,因为
,因为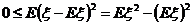 ,则
,则
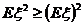 . (1.1.1)
. (1.1.1)
定理1.1.2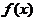 (Schwarz不等式)若
(Schwarz不等式)若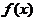 ,
,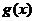 在
在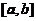 上可积,则
上可积,则
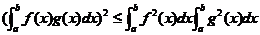 . (1.1.2)
. (1.1.2)
例1.1.1 若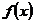 在
在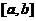 上非负连续,且
上非负连续,且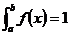 ,则
,则
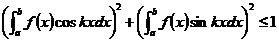 .
.
证明:法1应用Schwarz不等式求解式子左端,则
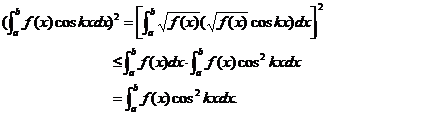
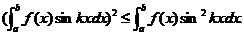
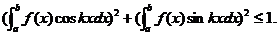 .
.
则
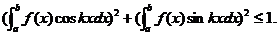
法2因为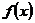 在
在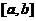 上非负连续,且
上非负连续,且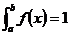 ,则依据概率密度函数定义,
,则依据概率密度函数定义,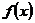 为随机变量
为随机变量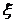 的密度,
的密度,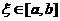 .
.
令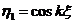 ,
,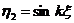 ,所以
,所以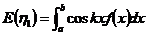 ,
,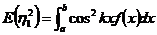 ,
,
且因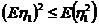 ,则
,则
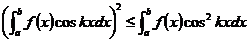 . (1.1.3)
. (1.1.3)
同理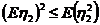 ,所以
,所以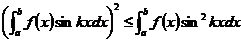 . (1.1.4)
. (1.1.4)
由(1.1.3)与(1.1.4)得
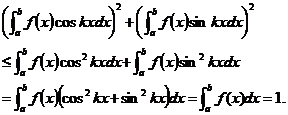
法1利用Schwarz不等式直接证明上述不等式,求解过程简单,但如果不熟悉Schwarz不等式,那么求证起来会很困难.法2将不等式赋予概率论的性质,解题过程更加清晰易懂,有助于问题的理解.
1.2利用詹森不等式证明不等式
剩余内容已隐藏,请支付后下载全文,论文总字数:8617字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


