论文总字数:13931字
目 录
1引言……………………………………………………………………5
2四色定理的几代计算机证明概述……………………………………6
2.1第一代证明 6
2.2第二代证明 7
2.3第三代证明 7
2.4几代证明总结 7
3几种四色定理非计算机解法探究……………………………………8
3.1利用数学归纳法证明四色定理 8
3.1.1方法概述 8
3.1.2方法分析总结 9
3.2利用图论中平面的欧拉公式来证明四色定理 9
3.2.1方法概述 9
3.2.2方法分析总结 11
3.3将图论与数学归纳法结合的证明方法 11
3.3.1方法概述 11
3.3.2方法分析总结 11
4探究四色定理的意义及其应用………………………………………11
4.1探究四色定理对数学与计算机科学共同发展的意义 11
4.2探究四色定理对图论发展的意义 12
5结论及讨论……………………………………………………………14
参考文献…………………………………………………………………15
致谢………………………………………………………………………16
四色定理的探究
魏斯宇
,China
ABSTRACT: Four-Color Theorem is one of three-largest mathematical conjecture in the world and it is a difficult problem for many years. So far, the four-color theorem has not been proved that a non-computer solution can be widely recognized by the mathematical community. This paper is divided into three parts, respectively from three aspects of the four-color theorem of research: the first part describes the process of proposed and development about four-color theorem, summarize the characteristics and impacts of respective four-color theorem after the third generation computer solution; the second part presents four-color theorem of the three kinds of non-computer solution and analyze the respective advantages and disadvantages of the solution; the third part discusses the practical significance of four-color theorem, and give an example to analyze the important significance about four-color on theorem progress of computer science and the graph theory development. Four-color theorem contains a wealth of mathematical thinking and logical thinking, has a very high practical significance and research value, it is worth to continue to explore.
Key words: four-color theorem non-computer solution graph theory
1.引言
四色定理又被称为四色猜想、四色问题,是世界三大数学猜想之一。它被人称为是图论中、甚至是整个数学中最难的问题之一。这与四色定理简洁、平凡的论述形成了非常鲜明的对比。四色定理通俗的说法是:每个平面地图,不管划分多少地理单元,可以只用四种颜色来染色,保证两两邻接区域的颜色不相同,(如示意图1-1所示,每个数字代表一种颜色)。它的理论看似容易,以至于可以向任何一位没有数学研究经历的平常人解释清楚;证明它却又如此之难,难到令多少位伟大的数学家困惑不已。从四色定理中散发出的数学研究的魅力,令人心驰神往,这也是笔者撰写此文的初衷。本文从四色定理的提出和发展出发,探讨了四色定理研究的历史意义和现实价值,着重于分析和研究四色定理的几种富有鲜明数学特点的非计算机解法,旨在能从这些证明方法中总结数学思想与方法,为后人的学习和研究提供帮助。
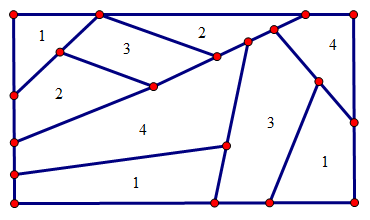
1-1四色定理示意图
1852年,毕业于伦敦大学的葛斯瑞来到一家单位进行地图着色的相关工作时,发现一个奇妙的现象:每幅地图都可以只用四种颜色着色。平时就热爱数学研究的葛斯瑞开始思考:这个现象能不能运用数学知识加以严格证明呢?他决定对这个现象进行研究。但几个月之后,他的研究工作却没有任何进展。之后,他曾向著名数学家德摩根、物理学家汉密尔顿等人求助,但他的问题并没有得到重视。
1873年,英国当时最著名的数学家凯莱在他的文章中,第一次从数学角度明确陈述了这一猜想,指出了证明这一猜想的要点和困难性,并承认自己“还无法给出证明”。他的论文引发了数学家们强烈的求解欲望,四色猜想成为了世界数学界最关注的问题之一。在当时一个普遍的观点是,四色定理看起来并不复杂,应该很快就能得到解决。然而事实却并非如此。经过了一个世纪,历经许多次尝试与否定,仍然没有人能准确地证明四色猜想。
1878年,著名的律师兼数学家肯普提交了证明四色猜想的论文,宣布证明了四色定理,但在之后被证明是错误的。不过他的思想方法为后人铺平了道路,四色定理的第一代证明就是建立在他的理论基础上的。
正当全世界的数学家被这个问题困扰之时,电子计算机的出现和普及改变了局面。1976年,美国数学家阿佩尔与哈肯在电子计算机上,用了1200个小时,作了100亿次判断,终于宣布完成了四色定理的证明,轰动了当时整个数学界。不过在当时这个证明方法并未获得数学界的一致认同,原因在于证明中使用了计算机,关键步骤无法进行手算核实。在那个计算机技术刚刚萌芽的时代,无法进行手算核实的计算机解法是不被信任的。现在,人们把阿佩尔和哈肯的证明方法称作四色定理的第一代证明。第一代证明当时虽被广泛质疑,但现在来看却有着重要的时代意义:阿佩尔和哈肯提出的计算机证明方法是人类第一次运用计算机技术证明著名数学猜想。从这之后,计算机证明开始被广泛地运用于各种数学难题的解决过程中。
1994年,四位数学家西缪尔、罗伯逊、桑德斯和托马斯提出了第二代证明。第二代证明虽然也使用了计算机,但它对第一代证明过程中的试错过程进行了简化,达到了人工进行复核的条件。第二代证明得到了数学界的普遍认可,但该证明方法隐藏在计算机内部的逻辑步骤仍然不够透明。
第二代证明发表十年后,英国剑桥大学的贡蒂埃以它为基础,提出了一种新的证明方法,将计算机证明过程的每一个逻辑步骤都完成了证明与复核,这就是现如今最为数学界所承认的第三代证明。下面我们来简要的概括分析一下四色定理几代证明的内容与思想方法。
2.四色定理的几代计算机证明概述
2.1第一代证明
1879年,肯普宣称他已经证明了四色定理。他运用欧拉公式,证明任意地图都至少伴随有一个需要同样多颜色的正规地图,因此,他只需对正规地图证明四色。但他还是无法克服四色问题的最大难点之——研究对象是无穷多个地图。在一段时间的思考后,肯普使用了归谬法(也就是我们今天常用的反证法):假设存在需五种颜色才可以染色的正规地图,然后从该命题中寻找矛盾,从而证明四色定理。
在论证过程中,肯普引入了两个重要的概念:不可避免性和可约性。不可避免性是指任意正规地图至少有一国具有2-5个邻国,2-5个邻国的构型是不可避免的。而可约性,是指从正规地图中移去某一个子图,所得新图的四色性蕴含原图的四色性。肯普当时认为,只要能够证明不可避免集中的每个构型都是可约的,四色定理就能被证明。而这两个概念为后人的求解作出了巨大的帮助。
之后,对事先假定的五色地图,他分成了存在二、三、四、五个邻国的四种情况来检查构造的可约性。我们可以看出,如果以上四种情况都可约,就与需要五种颜色产生矛盾,从而能够证明四色定理成立。但是,肯普在证明过程进行到存在五个邻国的情况时却失败了。虽然肯普失败了,但他的研究成果却让后人受益非浅。后来,希伍德通过修补肯普的证明过程得到了著名的五色定理。肯普的研究成果还为后人指明了方向:寻找可约构型的不可避免集。
1950年,一位名叫希什的数学家猜测存在一个有限的可约构型的不可避免集,而且其中构型的个数有一个上限——约一万。他把证明构型可约性的现有方法形式化,提出至少有一种方法在原则上是计算机所能完成的纯机械过程。希什对四色定理的研究作出的最大贡献,来自他发明的一种叫做放电法的方法。希什利用放电法,来寻找构型的不可避免集。根据前人的研究,希什发现,若一个图不可四色,那么图中必定存在某个局部障碍。希什发明放电法目的,就是要把这些局部障碍列为一个清单。他在研究中发现,这些障碍恰好是肯普所谓的“不可避免的构型”。希什在肯普研究的基础上进行了深化和改进,他的成果为之后人们利用计算机寻找可约构型提供了坚实的理论基础。希什也是第一位把计算机理论与技术运用到四色定理求解中的数学家。阿佩尔和哈肯在之后的研究工作中表示,他们的工作受到了希什研究成果的很大启发。
1972年,阿佩尔与哈肯合作,开始进行四色定理的研究。从希什的经历中,他们意识到了计算机辅助对证明过程的重要性。他们在充分考虑了运算机时后,合理地简化了问题。之后,他们在希什的基础上,提出了一种新的放电程序,构造了一个含有1936个构型的不可避免集。最终,阿佩尔和哈肯在在当时的巨型计算机上耗费了上千个小时,完成了构型可约性的证明。后来,他们又将可约构型的不可避免集的个数减少到了1482个。1976年6月,阿佩尔和哈肯宣布,四色定理已经被他们证明。
阿佩尔和哈肯的证明过程震惊了整个数学界。人们开始意识到,计算机不仅可以用来进行复杂的运算过程,更可以用于数学逻辑的证明。然而他们的证明方法也受到很多人的质疑,原因在于他们的方法本质上使用的是穷举法检验了几百万种情况。显然,这种方法具有不可复核性和不透明性,与传统的数学证明方法背道而驰。一代证明的两大派别“支持派”与“质疑派”彼此各执一词,象征着计算机辅助的证明方法此时还未被广泛接受。
剩余内容已隐藏,请支付后下载全文,论文总字数:13931字
相关图片展示:
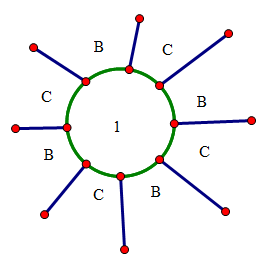
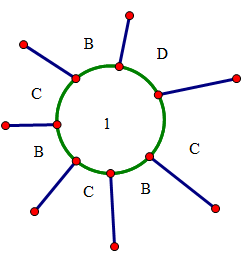
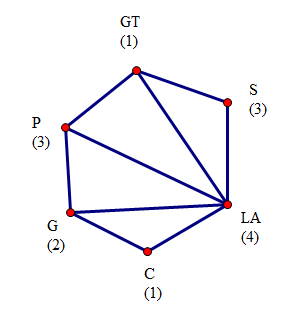
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


