论文总字数:7532字
目 录
0、引言 4
1、高阶等差数列的定义 4
2、高阶等差数列的通项公式 6
2.1定义法求通项公式 6
2.2公式法求通项公式 7
2.3待定系数法求通项公式 8
3、高阶等差数列的前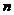 项和以及求和公式 8
项和以及求和公式 8
3.1定义法求和 9
3.2待定系数法求和 10
3.3拓展:利用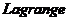 差值公式求和 13
差值公式求和 13
4、高阶等差数列的应用 14
参考文献 16
致谢 17
高阶等差数列
陈瑀
,China
Abstarct:Firstly,the paper narrates the defination of high order arithmetic progression through the concept of the arithmetic progression we learned in high school.After that,we start to explore the general term formula of high order arithmetic progression through the examples,in addition,it’s important to explore how to get the general term formula of high order arithmetic progression.Then,we begin to mainly discuss the sum of the former n terms of high order arithmetic progression,and take some examples to study the properties of high order arithmetic progression.At the same time,we also list the corresponding methods and steps to solve problems.Finally, we list the related application of higher order arithmetic progression.
Key words:arithmetic progression;high order arithmetic progression;the general term formula of high order arithmetic progression;the sum of high order arithmetic progression.
0、引言
在初高中的学习中,我们只是系统的学习了“等差数列”和“等比数列”.当然,除了最基本的“等差”“等比”数列,我们也接触过”非等比”以及“非等差”数列的前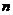 项求和以及求它的通项.“高阶等差数列”就是其中一类.所以,在该文章中我将会就“高阶等差数列”做一些相关的陈述和探究.其中,“高阶等差数列”的通项式和求和公式将会是我着重分析的部分,基本概念和实际应用部分也会做出详细的个人见解.
项求和以及求它的通项.“高阶等差数列”就是其中一类.所以,在该文章中我将会就“高阶等差数列”做一些相关的陈述和探究.其中,“高阶等差数列”的通项式和求和公式将会是我着重分析的部分,基本概念和实际应用部分也会做出详细的个人见解.
1、高阶等差数列的定义
研究数学课题,概念是第一位的.要研究“高阶等差数列”,不妨先从“差数列”入手.
定义1:给定一个数列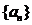 ,假设从第二项开始,依次减去它的前面的一项,可得出一个新的数列
,假设从第二项开始,依次减去它的前面的一项,可得出一个新的数列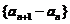 ,记作
,记作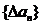 ,我们可以称它为原数列
,我们可以称它为原数列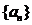 的一阶差数列,可以称它为一阶差.接下来,继续对一阶差数列
的一阶差数列,可以称它为一阶差.接下来,继续对一阶差数列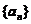 再进行求差,则把
再进行求差,则把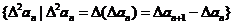 称做为原数列
称做为原数列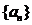 的二阶差.以此类推,可以求得三阶差,四阶差….{其中,
的二阶差.以此类推,可以求得三阶差,四阶差….{其中,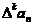 的
的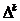 不是表示幂的意思,只是表示
不是表示幂的意思,只是表示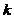 阶差的符号}
阶差的符号}
借着“差数列”的定义,接下来引入“高阶等差数列”的内容.
定义2:若某数列的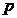
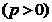 阶差是一组不为零的常数列,那么叫它是
阶差是一组不为零的常数列,那么叫它是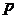 阶等差数列.
阶等差数列.
定理1:数列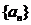 是
是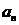 阶等差数列的充分必要条件是其通项
阶等差数列的充分必要条件是其通项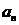 可以表示成
可以表示成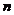 的
的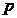 次多项式.其中,我将定义一个
次多项式.其中,我将定义一个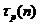 用来表示通项
用来表示通项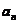 ,即
,即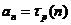 .
.
【证明】 充分性:若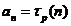 ,则
,则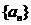 为
为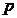 阶等差数列.我们可以用数学归纳法来证明.
阶等差数列.我们可以用数学归纳法来证明.
设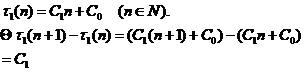 ,则有
,则有
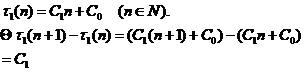
所以,当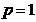 时,
时,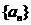 为一阶等差数列.
为一阶等差数列.
此外,设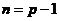 时命题也成立,即当
时命题也成立,即当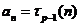 时,
时,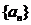 为
为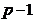 阶等差数列.假设存在一个
阶等差数列.假设存在一个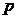 次多项式:
次多项式: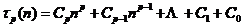 .
.
可以得出: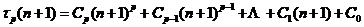
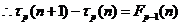 为一个有关
为一个有关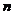 的
的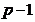 次多项式,所以可得
次多项式,所以可得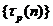 是一个
是一个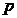 阶等差数列,即当
阶等差数列,即当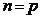 时也成立.由此可知,命题对于一切自然数
时也成立.由此可知,命题对于一切自然数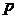 均能成立.
均能成立.
必要性:假设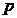 是
是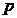 阶等差数列,则有
阶等差数列,则有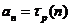 .
.
设数列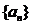 为:
为: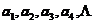 ,则一阶差数列为:
,则一阶差数列为: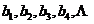
二阶差数列为: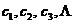 ,三阶差数列为:
,三阶差数列为: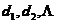 ,
,
剩余内容已隐藏,请支付后下载全文,论文总字数:7532字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


