论文总字数:7745字
目 录
摘要 ··················································1
引言 ··················································3
1 无穷量与等价无穷量 ··································4
2 等价无穷量替换定理推广 ·······························5
2.1 在极限式中有加、减运算的等价无穷量替换 ··················5
2.2 涉及变上限积分函数的等价无穷量替换 ····················8
2.3 涉及幂指函数不定式的等价无穷量替换 ······························9
3 等价无穷量在极限中的应用 ····························9
总结 ·············································11
参考文献 ·········································11
致谢 ················································· 13
等价无穷量在极限中的应用
蔡 贵
.
Abstract: Substitution of Equivalence Infinitesimal is one of the most important methods for the limits. Usually mathematical analysis textbooks only give us the product and quotient forms of equivalent Infinitesimal Substitution Theorem, which only has a smaller range of application. In this paper, we do a variety of promotion, thereby expanding the theorem applicable scope, so as to be applied to the infinitive of sun and difference consisting of two equivalence infinitesimal or a limited number of equivalence infinitesimal, the infinitive of power and exponential functions and the infinitive of variable limit integrals. Using the extended theorems in the limits can simplify the solving steps, which makes the calculations more flexible and convenient.
Key words: infinite quantity; equivalent infinite quantity; limit; L'Hospital Rule.
引言
函数极限是数学分析中最基本的知识点,也是学习的重点与难点. 在这些求极限的问题中,不太不好处理的便是 型,
型,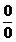 型这类不定式的极限,通常我们容易想到的方法就是以导数为工具的洛必达法则. 洛必达法则是以柯西中值定理为理论依据,它有一定的限制条件,对于某些问题可能会越用越复杂,并且出现循环. 例如,一个求如下
型这类不定式的极限,通常我们容易想到的方法就是以导数为工具的洛必达法则. 洛必达法则是以柯西中值定理为理论依据,它有一定的限制条件,对于某些问题可能会越用越复杂,并且出现循环. 例如,一个求如下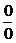 型的不定式极限:
型的不定式极限: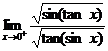 ,若用洛比达法则求解,则有:
,若用洛比达法则求解,则有:
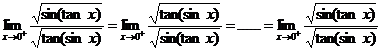 .
.
该计算过程出现了循环,得不到明确结果,洛必达法则在这并不适用. 若我们改用等价无穷小量替换来求解,由于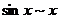
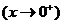 ,
,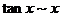
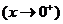 ,因而
,因而
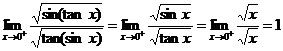 ,
,
该计算过程十分简单明了. 该实例充分体现了等价无穷量替换的便利性与实用性,往往能够正确有效地得出结果.
但在现行很多数学分析教材中,通常只给出了两个无穷小量的等价替换定理,该定理的适用范围也只限于积与商的形式,对极限式中的相加或相减的部分并不适用. 如极限问题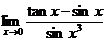 ,若由
,若由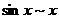
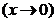 ,
,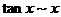
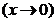 ,则推出
,则推出
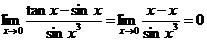
这样一个错误的结果. 既然等价无穷小量不能随意替换,那么在什么样的情况下可以替换,替换条件是什么?例如,在涉及和差的不定式中替换条件是什么?对于幂指函数形如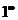 ,
,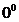 ,
,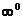 形式的不定式极限,还有涉及变上限函数积分不定式极限,计算时能否用等价无穷小量来替换呢?这些问题在很多教材里都没有具体的体现. 然而,我们在学习的过程中却常常遇到此类问题.
形式的不定式极限,还有涉及变上限函数积分不定式极限,计算时能否用等价无穷小量来替换呢?这些问题在很多教材里都没有具体的体现. 然而,我们在学习的过程中却常常遇到此类问题.
本文在已有基本知识点的基础上对定理进行了多方面的推广,扩大了定理的适用范围,使之适用于由两个或有限个无穷小量和与差组成的不定式,幂指函数不定式以及由变限积分组成的不定式.,对我们所学的知识做了一定的补充和完善.
作为预备知识,本节根据《数学分析》教材给出无穷小量,无穷大量的概念以及相关性质.
1 无穷量与等价无穷量
定义1.1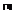 设
设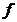 在某
在某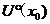 内有定义. 若
内有定义. 若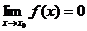 ,则称f为当
,则称f为当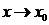 时的无穷小量.
时的无穷小量.
类似地定义当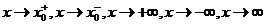 时的无穷小量.
时的无穷小量.
定义1.2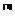 设当
设当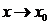 时,
时,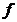 与
与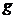 均为无穷小量, 若
均为无穷小量, 若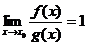 ,则称
,则称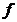 与
与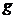 是当
是当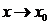 时的等价无穷小量. 记作
时的等价无穷小量. 记作 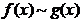
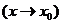 .
.
定理1.1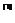 设函数
设函数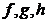 在
在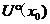 内有定义,且
内有定义,且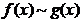
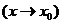 ,
,
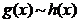
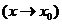 .
.
(i) 反身性: 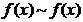
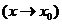 ,
,
剩余内容已隐藏,请支付后下载全文,论文总字数:7745字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


