论文总字数:4695字
目 录
1前言·····················································3
1.1超几何级数简介···························································3
1.2三次超几何级数恒等式·····················································4
2新超几何级数恒等式Ⅰ的证明·······························5
3新超几何级数恒等式Ⅱ的证明·······························7
4结论·····················································9
5讨论·····················································9
参考文献··················································9
致谢······················································11
两个新的超几何级数恒等式的证明
李欣
,China
Abstract:Generalized hypergeometric series is an important branch of special function and is closely related to combinatorics. It has important theoretic value and wide-ranging application in number theory, theoretical physics and computer algebra. In this article two new hypergeometric series identities are proved through four known cubic hypergeometric series identities.
Key words:generalized hypergeometric series; cubic hypergeometric series
1前言
1.1超几何级数简介
称关于变量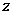 的幂级数
的幂级数
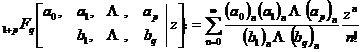
为超几何级数[ 1,2],其中 和
和 分别称为分子参量和分母参数,
分别称为分子参量和分母参数,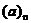 :=
:=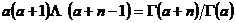 称为
称为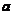 的
的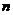 次升阶乘.这里的
次升阶乘.这里的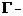 函数是由Euler积分给出的,即当
函数是由Euler积分给出的,即当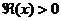 时,
时,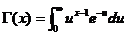 .需要注意的是
.需要注意的是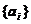 和
和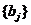 均为复参数并且保证分母中不出现零因子.为表述方便,我们通常使用以下符号来表示多个升阶乘和
均为复参数并且保证分母中不出现零因子.为表述方便,我们通常使用以下符号来表示多个升阶乘和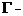 函数的分式形式
函数的分式形式
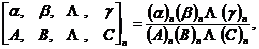
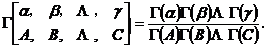
“超几何”这一名词源于希腊语,最早是英国牛津大学教授John Wallis在他的著作《Arithmetica Infinitorum》中研究了级数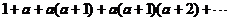 ,并称之为“超几何”级数,以区别于普通的几何级数,在其之后,很多数学家研究了与之类似的级数,特别是数学家C. F. Gauss在他的著作中给出了含有三个参变量的Gauss级数的定义
,并称之为“超几何”级数,以区别于普通的几何级数,在其之后,很多数学家研究了与之类似的级数,特别是数学家C. F. Gauss在他的著作中给出了含有三个参变量的Gauss级数的定义
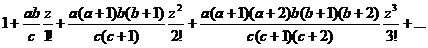 ,
,
并引入符号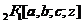 表示. Swiss L. Euler也给出了下述著名的关系式
表示. Swiss L. Euler也给出了下述著名的关系式

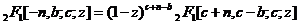 .
.
Vandermonde于1770年给出了一种推广的二项式定理:

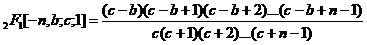 .
.
1812年,Gauss在他的博士论文“Disquisitiones generales circa seriem infinitam”中给出了超几何级数的定义,并同时证明了现称为“Gauss求和定理”的著名定理,即
 ,其中
,其中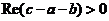
1836年,E.E.Kummer首次将“超几何”这一专业术语用于级数
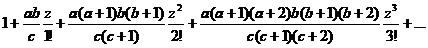 ,
,
并证明了Gauss函数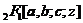 为二级微分方程
为二级微分方程

的解,指出这种类型的解共有二十四个,即Kummer24解.之后越来越多的数学家投入到了超几何级数的研究中,大家开始逐渐推广Gauss级数.Clausen首先采取了通过增加参数的方式来推广Guass函数,他研究了包含3个分子参量和2个分母参量的一类超几何级数.更多的关于超几何级数的著名求和定理被Dixon和Dougall等人给出.二十世纪初Bailey和Whipple在一系列的研究工作中完成了对超几何级数理论的比较完整的分析和完善,尤其是1935年Balley出版了专著《Generalized Hypergeometric Series》,详细介绍了一般超几何级数理论,并将之作为对Bailey著作的补充和完善,Slater于1966年出版专著《Generalized Hypergeometric Functions》,这两本著作也是介绍一般超几何级数理论最全面的著作.
1.2三次超几何级数恒等式
具有如下结构的超几何级数
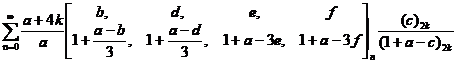 ,
,
称为三次超几何级数.
目前已知的两个非终止型的三次超几何级数恒等式有
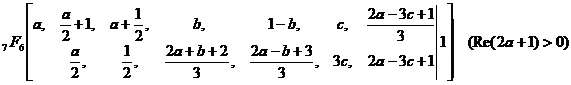
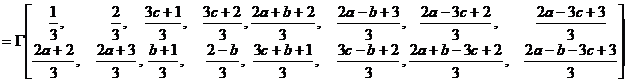 , (1)
, (1)
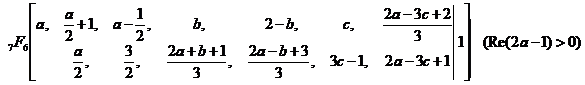
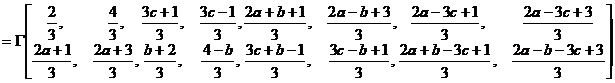 . (2)
. (2)
其中(1)式是Gosper(1977)在给Askey的信中给出的一个猜想,后被Gasper-Rahman[3]通过建立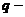 模拟的方式证明,同时Gasper-Rahman还发现了三次超几何级数求和公式(2).此外,2015年wang[5,6]利用Abel分部求和法分别给出了上述两个三次超几何级数求和公式一个新的简短的直接证明.等式(1)和(2)对应的终止型求和公式[7]是
模拟的方式证明,同时Gasper-Rahman还发现了三次超几何级数求和公式(2).此外,2015年wang[5,6]利用Abel分部求和法分别给出了上述两个三次超几何级数求和公式一个新的简短的直接证明.等式(1)和(2)对应的终止型求和公式[7]是
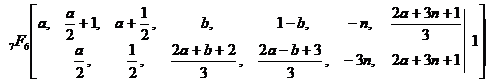
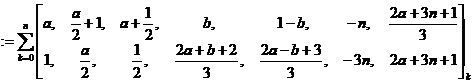
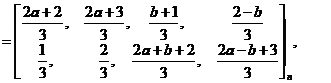 (3)
(3)
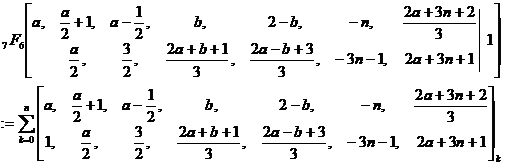
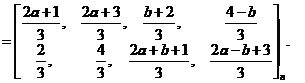 (4)
(4)
需要注意的是(3)和(4)并非(1)和(2)分别在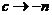 时的特殊情况,本文主要通过分析非终止型超几何级数恒等式(1)和(2)在
时的特殊情况,本文主要通过分析非终止型超几何级数恒等式(1)和(2)在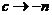 时的情况,结合终止型级数恒等式(3)和(4),来推导两个新的非终止型的超几何级数恒等式.
时的情况,结合终止型级数恒等式(3)和(4),来推导两个新的非终止型的超几何级数恒等式.
2新超几何级数恒等式Ⅰ的证明
定理1 对于满足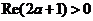 的任意实数
的任意实数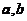 ,有如下求和公式成立
,有如下求和公式成立
剩余内容已隐藏,请支付后下载全文,论文总字数:4695字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


