全概率公式和贝叶斯公式的应用

论文总字数：10898字

目 录

1 引言………………………………………………………………………1

2 全概率公式和贝叶斯公式的定义………………………………………2

2.1 全概率公式的定义…………………………………………………………………………2

2.2 贝叶斯公式的定义…………………………………………………………………………3

3 全概率公式和贝叶斯公式的应用………………………………………4

3.1 全概率公式和贝叶斯公式在医学上的应用………………………………………………4

3.1.1诊断甲状腺疾病………………………………………………………………………5

3.1.2普查肝癌………………………………………………………………………………5

3.2 全概率公式和贝叶斯公式在信号传输方面的应用………………………………………6

3.2.1通信系统的信号传输…………………………………………………………………7

3.3 全概率公式和贝叶斯公式在概率推理方面的应用………………………………………8

3.3.1交通工具的概率推理…………………………………………………………………8

3.4 全概率公式和贝叶斯公式在经济方面的应用 ……………………………………………9

3.4.1不合格品的概率 ……………………………………………………………………10

3.4.2责任分担问题 ………………………………………………………………………10

4 结论……………………………………………………………………11

5 参考文献………………………………………………………………12

6 致谢……………………………………………………………………13

全概率公式与贝叶斯公式的应用

袁维逍

，China

Abstract：The total probability formula and Bayes formula are two basic formulas in probability theory and mathematical statistics, by which the probability of a more complex event can be detemined by the probability of some simple events. Therefore, these formulas have been widely used in medicine, economics and other modern research.This paper introduces the definition of total probability formula, Bayes formula and their related theory, and then supplies specific examples to show their applications in medical, signal transmission, probabilistic inference, economic and other aspects. Finally, a comprehensive summary is given to to the application methods and rulls of the both formulas.

Key words：The total probability formula; The Bayes formula; Application

1 引言

概率论是概率统计的基础，在概率论里有两个非常重要的公式，它们是全概率公式和贝叶斯公式，它们在各个领域都有着非常广泛的应用。全概率公式和贝叶斯公式自身就包含了非常深刻的数学思想，但对于刚开始学习概率论的同学来讲，主要难点是对公式的理解及其应用。虽然公式形式简单，但是想要将它们理解透彻并能熟练应用，还是有必要进行深入地理解和全面的总结。

由简入繁、由易知难是解决数学问题的重要思想。当遇到一个比较抽象、复杂且不易入手的事件时，若能将这个复杂事件分解为若干个互不相容的简单事件的和，通过计算每个简单事件的概率以求解原复杂事件的概率，这便是全概率公式运用的思想。

贝叶斯公式主要用来计算复杂事件的概率,它本质上是乘法公式和加法公式的综合运用。贝叶斯公式在17世纪出现，从刚发现到如今，已经深入到社会和科学的各个方面。它是在观察到事件已经发生的前提下，寻找导致其发生的每个原因的概率。贝叶斯公式在实际生活中有广泛的应用，它能帮助人们确定某结果发生的可能性最大的原因。

当今社会正在飞速地发展中，市场竞争日益强烈，决策者必须综合考虑以往的信息及现状再作出综合判断，决策概率分析变得越来越重要。在决策概率分析中，有一种决策称为贝叶斯决策，它是通过贝叶斯公式来进行概率判断的。贝叶斯公式主要用来计算先验概率与后验概率，是实行决策的重要工具，在解决医学、市场预测、信号估计、概率推理以及产品检查等不确定问题上有非常重要的应用。

在科技和工程中的众多交叉领域中，对于全概率公式和贝叶斯公式的研究和应用引起了国内外众多学者的兴趣，取得了大量的成果。夏敏轶、张焱在2006年发表了《贝叶斯公式在风险决策中的应用》，文中在金融领域中应用了贝叶斯公式，通过分析在风险决策中信息的作用，利用贝叶斯公式提供了方法来确定信息价值和提高风险决策的可靠性。李新军、刘晓明、黄松、夏洪亚在在2009年发表了《基于贝叶斯公式的软件缺陷模型研究》，文中在军事通讯技术中应用了贝叶斯公式，构想出一种软件缺陷模型，它的基础是根据贝叶斯公式提出的贝叶斯网络理论，根据分析软件中存在缺陷的对象之间相互影响的关系建立了贝叶斯网络模型，通过现有的经验数据评估贝叶斯网络模型中各节点的缺陷概率分布，利用贝叶斯公式分析了导致结果发生的影响因素，并在实际项目中应用该模型，且取得了良好的效果。该模型为往后的开发项目提供了一定的经验数据，预防再次发生同样的错误。张全超、李海燕在2009年发表了《基于贝叶斯公式的诊断模型》，在医疗体系中应用了贝叶斯公式，从一个颇具争议的诊疗案例出发，以贝叶斯公式为基础，结合我国现阶段的医疗体制，构建了一个定量化的诊断模型，得出诊疗方案合理性的指标，通过经验数据检验了模型，并评估了该模型，更加证明在我国建立医疗责任保险制度是非常紧迫和必要的。这些成果充分证明了全概率公式和贝叶斯公式强大的应用价值和广阔的应用前景。

本文在深入理解全概率公式和贝叶斯公式的基础上，全面、系统介绍了全概率公式和贝叶斯公式在医学、信号传输、概率推理和经济决策方面的应用。这些应用对于加深理论知识的理解、体现数学的应用价值方面有重要的现实意义。

2 全概率公式和贝叶斯公式

2.1全概率公式

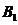
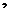
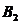
定理^[1] 设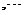是一列互不相容的事件，且有

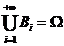
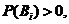
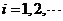
则对任一事件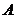，有

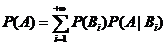（1）

公式（1）通常称作全概率公式，它是概率论中最基本的公式之一。

证明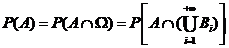

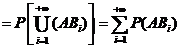
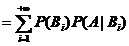
注1：运用全概率公式来解题的一般步骤为：

（1）确认题目中要求的事件,然后依照题设来将所求的事件正确分解开来；

（2）将已知数据一一罗列出来；

（3）在全概率公式中代入已知数据,求出。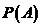

在解题过程中应当注意不要被问题的表面所迷惑。很多问题并不是只简单地代全概率公式就能解决的。

在应用全概率公式解比较复杂抽象的问题时,先要具体化这些问题,才能达到简化题目的目的，使得我们能够更简单的解决这些问题。

运用综上所述解题方法,能够解决需要运用全概率公式的更加复杂的实际问题。

2.2贝叶斯公式

定理^[1] 若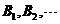为一列互不相容的事件，且

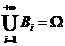
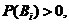
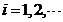
则对任一事件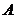，有

剩余内容已隐藏，请支付后下载全文，论文总字数：10898字