论文总字数:13069字
目 录
摘要…………………………………………………………………1
Abstract…………………………………………………………………2
1引言………………………………………………………………………3
2数值格式的构造………………………………………………………4
2.1 时间分裂法………………………………………………………………………………4
2.2 非线性子问题的精确解…………………………………………………………………6
2.3 可直接积分的线性子问题一的求解……………………………………………………8
2.4 紧致差分法求解线性子问题二…………………………………………………………8
2.5 具体的数值格式…………………………………………………………………………11
3数值结果分析…………………………………………………………12
4结束语…………………………………………………………………16
参考文献…………………………………………………………………17
致谢………………………………………………………………………19
二维复值金兹堡-朗道方程基于时间分裂的
四阶紧致交替方向隐格式
朱晨怡
,China
Abstract:This paper design a time splitting fourth-order compact alternating direction implicit (ADI) finite difference scheme for two-dimensional complex Ginzburg-Landau(GL) equation.At first, this paper divides the GL equation into one nonlinear and two linear subproblems by using time-splitting method,the nonlinear subproblem and one of the linear subproblem can be regarded as an ordinary differential equations which can be solved exactly by using direct integral calculation, then another linear subproblem is approximated by constructing a compact alternating direction implicit finite difference scheme.The proposed numerical method is of fourth-order accuracy in space and of second-order accuracy in time,respectively.At each time level just only several tri-diagonal system of linear algebraic equations need to be solved by Thomas method (i.e.,double-sweep method).Thus the proposed method is not only accurate but also efficient.Lastly,extensive numerical results are recorded to testify the accuracy and efficiency of this numerical method,and some dynamic behaviors of the GL equation are simulated.
Key words:2D complex Ginzburg-Landau equation;Time-splitting method;Compact finite difference scheme;Alternating direction implicit scheme
1 引言
在这篇文章中,我们对含有周期边界条件的二维复值金兹堡-朗道(Ginzburg-Landau)方程展开了如下研究
其中 是
是 上的有界域,
上的有界域, 、
、 分别是未知和给定的复值函数;参数
分别是未知和给定的复值函数;参数 ,
, ,
, ,
, 和
和 都是实数且
都是实数且 ,
, ;参数
;参数 是线性项的系数,当
是线性项的系数,当 ,
, 时,所有解
时,所有解 将趋于0.
将趋于0.
复值金兹堡-朗道(GL)方程为1950年由Ginzburg和Landau基于朗道二级相变共同构造出的一个描述超导理论的简化数学模型 .它在众多领域中描述了非线性系统的广泛应用,如非平衡流体动力学和化学系统,非线性光学和量子力学.它还能够对物质的超导、超流性,对流问题,物理相变过程和激光非线性波以及玻色-爱因斯坦凝聚现象等进行描述,具体参见文[2].当问题
.它在众多领域中描述了非线性系统的广泛应用,如非平衡流体动力学和化学系统,非线性光学和量子力学.它还能够对物质的超导、超流性,对流问题,物理相变过程和激光非线性波以及玻色-爱因斯坦凝聚现象等进行描述,具体参见文[2].当问题 中的
中的 时,复值金兹堡-朗道方程便是近几年以来被广泛议论的非线性薛定谔方程,因此越来越多的国内外数理理论学者对GL方程都展开了深入研究.其中,郭柏灵教授和他的学生们就对该类方程展开了非常系统深入的研究,包括该类方程的非齐次初边值问题、有限维行为、周期解的存在性、整体解的存在唯一性、整体吸引子的存在性等性质,详尽内容可参见文献[3]-[10].另外,文献[11]证明了GL方程带有初边值问题条件下的强解和弱解的存在性.文献[12]采用拟解法求解得到GL方程的暗孤子解同时还对其进行了稳定性分析.
时,复值金兹堡-朗道方程便是近几年以来被广泛议论的非线性薛定谔方程,因此越来越多的国内外数理理论学者对GL方程都展开了深入研究.其中,郭柏灵教授和他的学生们就对该类方程展开了非常系统深入的研究,包括该类方程的非齐次初边值问题、有限维行为、周期解的存在性、整体解的存在唯一性、整体吸引子的存在性等性质,详尽内容可参见文献[3]-[10].另外,文献[11]证明了GL方程带有初边值问题条件下的强解和弱解的存在性.文献[12]采用拟解法求解得到GL方程的暗孤子解同时还对其进行了稳定性分析.
虽然已有大量研究分析了复值金兹堡-朗道方程的精确解及其稳定性,但极少数情况可以获得该方程的解析解.一旦不存在解析解时,比如出现五次或更高次的代数方程,那么就需要运用数值方法来求解近似值.数值研究对方程的所有特征都可以有一个较为完全透彻的概括.针对复值金兹堡-朗道方程,对于一维情况,该方程的一种特殊情况便是Kuramoto-Tsuzuki(KT)方程,孙志忠在文献[13]中构造了KT方程的非线性隐式有限差分格式,并证明了该格式是无条件收敛于 的.此外,针对一维复值金兹堡-朗道方程的周期初值问题,文献[14]中张晶等人提出了一个收敛阶能达到
的.此外,针对一维复值金兹堡-朗道方程的周期初值问题,文献[14]中张晶等人提出了一个收敛阶能达到 的非线性三层紧致差分格式.对于二维情况,许秋滨等人在文献[15]-[16]中提出了该方程的时间分裂差分格式、半显式的线性两层差分格式和半显性三层差分格式,证明了上面三种线性化的差分格式均在
的非线性三层紧致差分格式.对于二维情况,许秋滨等人在文献[15]-[16]中提出了该方程的时间分裂差分格式、半显式的线性两层差分格式和半显性三层差分格式,证明了上面三种线性化的差分格式均在 处收敛.裴等人在文献[17]中对该方程的周期边界问题又构造了三个数值格式,得到二阶隐式差分格式和四阶紧致格式的精度都为
处收敛.裴等人在文献[17]中对该方程的周期边界问题又构造了三个数值格式,得到二阶隐式差分格式和四阶紧致格式的精度都为 ,谱方法的精度是
,谱方法的精度是 (m为方程的光滑度),并通过数值模拟分析了平面波解,表明了四阶紧致格式计算效果最好.为了增加高维格式的计算精度,文献[18]和[19]都引入了一种交替方向隐式法来计算我们所研究的方程,文献[19]中对处理后的方程提出了一个预测-校正格式,该格式主要是为了对非线性项进行复迭代处理,最终得到算法在空间方向具有四阶精度,时间方向具有二阶精度,虽然避免了解决非线性项并提高了精度,但是迭代仍有增加方程计算量的效果,依然会影响计算效率.
(m为方程的光滑度),并通过数值模拟分析了平面波解,表明了四阶紧致格式计算效果最好.为了增加高维格式的计算精度,文献[18]和[19]都引入了一种交替方向隐式法来计算我们所研究的方程,文献[19]中对处理后的方程提出了一个预测-校正格式,该格式主要是为了对非线性项进行复迭代处理,最终得到算法在空间方向具有四阶精度,时间方向具有二阶精度,虽然避免了解决非线性项并提高了精度,但是迭代仍有增加方程计算量的效果,依然会影响计算效率.
本文的主要目的就是基于时间分裂对二维复值金兹堡-朗道方程提出一个紧致交替方向隐式差分格式.该算法首先将GL方程分裂成了一个非线性子问题和两个线性子问题,对其中一个线性子问题以及非线性子问题均可视为常微分方程进行精确积分计算,然后对另一个线性子问题构造一个紧致交替方向隐差分格式来进行数值求解.该算法在时间和空间方向上分别具有二阶和四阶精度,其优点在于每一个时间层只需运用追赶法求解一族常系数三对角线性代数方程组,便可以得到较高的精度且较快的计算效率.
剩余内容已隐藏,请支付后下载全文,论文总字数:13069字
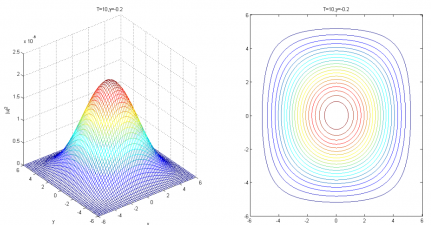
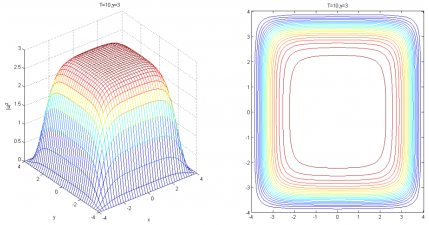
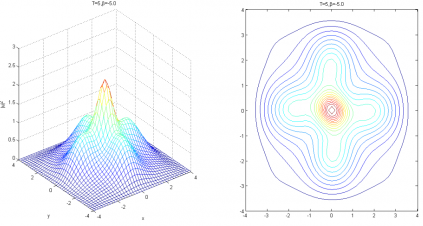
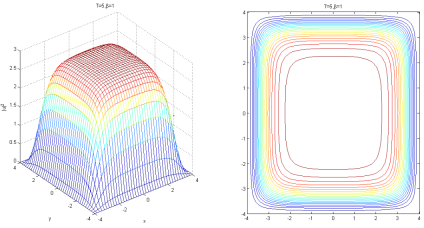
相关图片展示:
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;