论文总字数:10557字
目 录
0引言··················································3
1预备知识··············································3
1.1期权的定义 ··········································3
1.2概率论预备知识 ·······································4
2二叉树模型············································5
2.1单期二叉树模型 ·······································5
2.2多期二叉树模型 ·······································6
3二叉树模型的应用······································7
3.1二叉树模型在欧式期权中的应用·····························7
3.2二叉树模型的数值算例 ··································8
4关于二叉树模型参数的讨论······························11
参考文献·············································· 12
二叉树模型在期权类金融衍生产品的应用
代昕瑶
Abstract:In recent years,the applications of the mathematical model for the financial derivatives development and pricing problems play an important role.Because the option financial derivatives have good risk aversion and found value of the function,it has become the most active on the market of financial derivatives.This anthology choose the option pricing model with two binary tree representative models are discussed.Firstly,we introduce the two tree single period and multi period model;secondly,we discuss the application of two binary tree model in the European option and simulated;finally,we according to the numerical simulation results of two binomial tree model parameters to make some discussion.
Key words:Option pricing ;Two fork tree model;European option
0引言
在最初的金融市场上,人们能进行的投资行为相对与如今的市场而言比较单调.最初,人们进行的金融活动有银行存款、银行承兑汇票、债券和股票等几种形式.等到了二十世纪后,金融市场的发展开始发生巨大的改变,金融工具的数量和种类也在发生着极大的变化.金融市场一直在不断的发展,一直到了今天,除了原来的各种金融工具的发展逐渐成熟之外,新兴的金融产品得到迅猛发展.在众多迅猛发展的新兴金融产品中,而期权是其中最常用的一种金融衍生产品,详见[1-3].由于期权的发展迅猛,期权定价问题的研究十分有意义,随着数学模型在定价问题中的应用,使得这一问题得到了很好的解决.本文选择了期权定价模型中最具有代表性的二叉树模型并对其做出了一些研究,在此本文分为四部分:第一部分系统的介绍了期权的定义、期权定价的基本理论和一些概率论的知识;第二部分分析了二叉树方法的单期与多期模型;第三部分给出了二叉树模型在欧式期权中的定价方法,并进行了数值模拟;第四部分根据数值模拟结果讨论了二叉树模型的相关参数,并将它与原有参数进行了比较与分析.
1 预备知识
1.1期权的定义
期权是金融产品的衍生品的一种,但期权并不是一种独自存在的证券或者股票.通俗的说,期权相当于是一种买方和卖方一起达成的约定,约定的双方一方为买者,另一方就为卖者.在期权市场上,期权合约就相当于一种权利.这种权利使得合约的买方在规定的时间范围内可以用特定的价格买入标的资产,为了使合约达成,买方应该对卖方进行一些补偿.在合约达成之后,若合约的持有者即合约买方要买入资产,卖方应该同意交割出资产;若持有者要卖出资产,则卖方应该买入该资产.
期权合约中都会包涵以下四个内容:①标的资产.即期权合约中买卖的原生资产种类;②期权的行使价格.即期权合约中签订的资产买入价;③资产的数量;④期权合约到期日.期权种类的划分有两种方式,第一种是按照标的资产的购入和销售,期权可以划分为:①看涨期权,它是在约定的时间按一定的价格买入约定量的标的资产的合约;②看跌期权,它则是在约定的时间按一定的价格卖出约定量的标的资产的合约.第二种方式是按期权合约中事先约定好的条款来划分为:①欧式期权,在合约的到期日进行买卖;②美式期权,在合约的到期日之前包括到期日当天都可以进行期权买卖.详见[4].
期权合约的存在,就是为了能让买方和卖方能够获得利益,当期权的定价不同,合约双方获得的利益也会随之改变.所以期权定价的作用就显得尤为重要,下面我们将简单介绍期权一下定价.
我们就看涨期权和看跌期权来介绍期权定价.首先简单的对两种期权计算收益,假设合约敲定价格为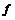 ,到期日为
,到期日为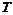 ,可以得到在到期日期权的收益
,可以得到在到期日期权的收益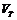 为
为
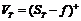 , (看涨期权)
, (看涨期权)
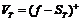 , (看跌期权)
, (看跌期权)
其中,到期日的价格为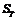 ,
,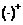 表示取最大值.
表示取最大值.
考虑看涨期权,从期权的收益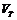 公式中可以看出,在到期日,如果
公式中可以看出,在到期日,如果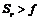 ,则期权合约购买者将用敲定价格
,则期权合约购买者将用敲定价格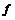 购买标的物;反之,若
购买标的物;反之,若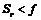 ,则该合约毫无意义.看跌期权也同样如此.由此,期权是一种收益不定的合约,是一种未定的权益.
,则该合约毫无意义.看跌期权也同样如此.由此,期权是一种收益不定的合约,是一种未定的权益.
虽然期权的定价决定于标的物价格的变化,由于标的物是一种有风险的资产,所以它的价格不是固定的而是随机的.但是,标的资产一旦确定价格,那么作为其衍生证券即期权的价格也会随之定下.所以期权的定价就相当于确定式子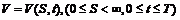 以及求解它.
以及求解它.
1.2概率论预备知识
命题1[5] 如果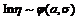 .即
.即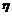 服从均值为
服从均值为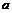 .标准差为
.标准差为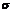 的对数正态分布.则
的对数正态分布.则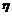 的均值和方差为
的均值和方差为
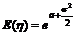 ,
,
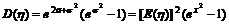 .
.
定义1[5] 设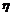 为随机变量.记
为随机变量.记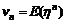 .则称
.则称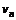 为
为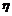 的
的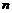 阶原点矩
阶原点矩
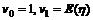 . (1)
. (1)
定义2[5] 设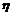 为随机变量.若
为随机变量.若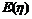 存在.设
存在.设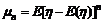 .则称
.则称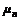 为
为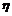 的
的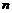 阶中心矩
阶中心矩
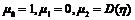 . (2)
. (2)
剩余内容已隐藏,请支付后下载全文,论文总字数:10557字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


