欧拉积分的性质及其应用

论文总字数：7492字

目 录

1 引言............................................................................................................................................3

2 欧拉积分的性质................................................................................... .............................3

2.1 B函数的性质.......................................................................................................................4

2.1.1 B函数的连续性.......................................................................................................4

2.1.2 B函数的常见性质....................................................................................................4

2.1.3 B函数的可微性........................................................................................................4

2.1.4 B函数的图像............................................................................................................5

2.2 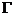函数的性质.....................................................................................................................6

2.2.1 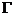函数的连续性......................................................................................................6

2.2.2 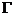函数的常见性质..................................................................................................7

2.2.3 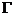函数的延拓..........................................................................................................7

2.2.4 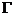延拓后的图像......................................................................................................8

2.2.5 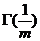的应用..........................................................................................................8

3 欧拉积分的应用.................................................................................................................9

3.1 欧拉积分在定积分中的应用.............................................................................................9

3.2 欧拉积分在重积分中的应用...........................................................................................10

3.3 欧拉积分在概率及数理统计中的应用...........................................................................11

结论...............................................................................................................................................13

参考文献....................................................................................................................................13

致谢...............................................................................................................................................14

欧拉积分的性质及其应用

马广琳

（，China

Abstract: The Euler integral is two very important non primary function defined by the improper integral with parameter variable. In this paper,we summarize the definition and properties of Euler integral and consider its applications in solving definite integral, multiple integral, Probablity Theory and Mathematical Statistics.

Keywords: Euler integral, definite integral, multiple integral, probability statistics

1引言

莱昂哈德·欧拉（Leonhard Euler）是十八世纪一位对数学界产生巨大影响的伟大的数学家， 他是一位全才数学家，他在数学方面的研究领域非常广泛，在数论、代数、微积分、几何学等领域作出了巨大的贡献.其著作浩如烟海，数量之多简直让人难以相信，他的许多书籍论文成为数学界的经典著作.欧拉对含参量的积分作了详尽、系统的研究，总结出了两类含参变量积分表示的非初等函数，即欧拉积分，并将其运用于实际问题，大大提高了解决问题的效率.欧拉积分的运用，对我们更好的学习和研究含参变量积分有着深远的影响.

近年来，许多作者对欧拉积分做了许多新的探索与讨论，1991年，冯云芬[1]对求解含参变量积分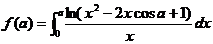所用的特殊方法做了一些改进，使得计算过程更加简捷. 2008年，赵经纬和王贵君[2]通过三类定积分计算问题，讨论了如何应用欧拉积分来计算某些难度较大的定积分，使得问题直观简洁，通俗易懂.2015年，卢路加，张君会，赵志稳[3]一些复杂的积分变成欧拉积分的形式，再巧妙应用伽马函数和贝塔函数的性质，将问题进行简化. 2009年，田兵[4]主要给出了一些例子，说明两个函数在实际运算中的重要作用,近期，孙兰香[5]主要利用函数构造法，借助欧拉积分的性质，表明了函数变换在解题中的重要作用，帮助我们进一步熟练掌握理论知识，值得我们学习.2014年，周晓辉[6]比较详细的证明了欧拉积分的基本性质以及两个函数之间的关系. 欧拉积分不仅运用在数学分析中，同时可广泛应用于概率及统计这门学科之中．例如在[7]和[8]中，利用了欧拉积分的性质可求解随机变量的一些相关问题，帮助我们更好的学习概率论及数理统计这门学科.[9]和[10]是欧拉积分在物理学中的运用，对于学习物理这门学科的相关知识也提供了方便.

在阅读了上述这些参考文献以后，本文首先给出欧拉积分具有的性质，然后论证两个函数之间的关系，最后通过举例的方式，来说明欧拉积分在定积分、重积分、概率统计中的应用，使一些复杂的题目计算起来更加简单，并且加对知识之间相互联系的理解.

定义[11] 含参量积分

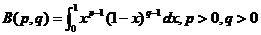， (1)

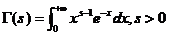(2)

分别称为第一类和第二类欧拉积分，或依次称为贝塔（Beta）函数（或写作B函数）和伽马 （Gamma）函数（或写作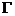函数）. 下面我们分别看Beta函数和Gamma函数的具体性质.

2 欧拉积分的性质

2.1 B函数的性质

2.1.1 B函数的连续性

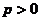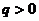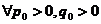B函数(1)的定义域为，.对，当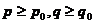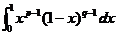，一致收敛，所以B函数在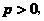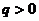上连续.

2.1.2 B函数的常见性质

剩余内容已隐藏，请支付后下载全文，论文总字数：7492字