论文总字数:14362字
目 录
0、引言 1
1、抽屉原理简述 1
1.1抽屉原理的一般形式 1
1.2抽屉原理推广的四种形式 2
2、抽屉原理的应用 3
2.1抽屉原理在数学竞赛中的应用 3
2.2抽屉原理在大学数学中的应用 6
3、应用抽屉原理的要点——构造抽屉 7
3.1利用自然数的不同分类构造抽屉 8
3.2利用划分构造抽屉 10
3.3根据问题的需要构造抽屉 13
3.4利用染色构造抽屉 14
3.5利用映射的概念构造抽屉 14
4、抽屉原理的反面——空巢原理 15
结语 15
讨论 15
参考文献 17
致 谢 18
抽屉原理及其在数学各科中的应用
郭子豪
, China
Abstract: Drawer principle is a powerful tool to prove the “existence”, which have a wide range of applications in math. But such a simple and obvious principle is not easy to apply, where the difficulty is in how to set the drawer. The actual problem is converted into constructing a drawer. This paper introduces the principle and general from of the four kinds of drawer principle and some application of drawer principle. Finally this paper introduces “principle of empty nest” which is the opposite of the drawer principle.
Key words: Drawer principle; drawer; construction
0、引言
利用抽屉原理是证明问题发生“必然性”的一个有力途径,它一般表现为:将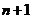 (或更多)个元素随机放进
(或更多)个元素随机放进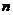 个抽屉中,那么一定会发生“有一个抽屉中出现不少于2个元素”的情况.
个抽屉中,那么一定会发生“有一个抽屉中出现不少于2个元素”的情况.
早在中国古代《晏子春秋》里就有一个“二桃杀三士”的故事:齐景公养着三名勇士:田开疆、公孙接和古冶子,所谓功高盖主并且他们也不懂得收敛,激起了齐景公的杀心,这时候晏子就给齐景公出了个主意:让齐景公赏赐给他们桃子,但是3个人只赏赐2个桃子,让他们自己根据功劳决定桃子归属,最终3名勇士不堪受辱而纷纷自刎.在这个典故中晏子巧妙的运用抽屉原理:两个桃子实际上就是两个“抽屉”,将三人放入其中一定会出现2人在同一抽屉的现象,即有一个桃子得让2个人吃.实际上,只要勇士们不能够放下面子吃同一个桃子,那么就已经落入了齐景公所设圈套之中.
看起来抽屉原理不是很难,但实际上它的作用确实很大,尤其体现在数学问题中.19世纪初德国数学家狄利克雷(1805—1859)最先利用抽屉原理来建立有理数的知识体系,并且慢慢应用到后面的引数论、集合论、组合论等数学分支中,所以为了纪念狄利克雷,抽屉原理也被叫做狄利克雷原理.1947年,抽屉原理开始被一些匈牙利数学家拿到数学竞赛中去.
有时候会有很多比较有意思或者复杂的数学问题,其他方法无从下手,但是如果用到抽屉原理困难之处就会隐忍而解,由此可见抽屉原理的灵活性.但是实际问题当中,如何用看起来简单明了的抽屉原理并不是很容易,难就难在如何把问题和抽屉原理联系起来,也就是说如何根据题目构造相应的抽屉,把一个要研究的问题转化为抽屉原理问题,也就是决定如何分类,构造抽屉并且发现该问题中隐含的与抽屉原理有关的条件来解决所求.
1、抽屉原理简述
1.1抽屉原理的一般形式
在研究数学题时,有很多必然性的相关问题,比如:“13个人当中一定有2个人出生在同一个月”;“某个学校368名学生当中,一定有2个学生一天生日”;“2017个人任意分成200个小组,肯定有一组人数多于10”;“把[0,1]内的所有无理数放到2017个集合中,至少有一个集合中含有无数个无理数”.这类确定性问题中,“确定”的含义是“绝对会发生”.在碰到这类问题的时候,一般只需要证明事件发生的必然性,而不需要纠结于事件发生的具体情况.这些问题一般不需要大量计算,主要侧重于分析,而这所用的数学原理就叫做抽屉原理..
看起来不是很难的抽屉原理,实际上它的作用确实很大,尤其体现在数学问题中.19世纪初德国数学家狄利克雷(1805—1859)最先利用抽屉原理来建立有理数的知识体系,并且慢慢应用到后面的引数论、集合论、组合论等数学分支中,所以为了纪念狄利克雷,抽屉原理也被叫做狄利克雷原理,当然还有人叫它“鸽巢原理”.这个原理可以简单地叙述为“往9个抽屉中放入10个苹果,则一定会出现一个抽屉中的苹果数大于或等于2的情况”.推广到一般形式为:
抽屉原理Ⅰ[1]把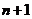 个元素按照任意确定的方式划分成
个元素按照任意确定的方式划分成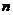 个集合,那么一定有某个集合含有两个或两个以上的元素.
个集合,那么一定有某个集合含有两个或两个以上的元素.
将原理Ⅰ再推广到一般形式:
抽屉原理Ⅱ[2]把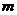 个元素按照任意确定的方式划分成
个元素按照任意确定的方式划分成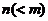 个集合,那么一定有某个集合含有
个集合,那么一定有某个集合含有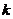 个或
个或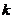 个以上的元素,其中
个以上的元素,其中
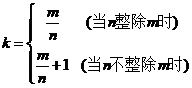
抽屉原理Ⅲ[3] 把无穷个元素按任一确定的方式分成有穷个集合,那么至少有一个集合中仍含有无穷多个元素.
上述三个原理都被称之为抽屉原理,相比于其他高深的数学原理,它还算通俗易懂的.然而,他的作用却远远不是表面所能表现的,从小学到高中乃至于大学的数学问题中,它都经常出现.而往往它解决的那一类问题都是一些比较灵活有趣,又难入手的题目.
1.2抽屉原理推广的四种形式
形式一 把一个整体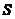 任意分成n份,那么至少有一份不少于
任意分成n份,那么至少有一份不少于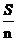 ,也至少有一份不多于
,也至少有一份不多于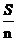 .
.
证明:(用反证法)假设都少于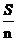 ,则总数少于
,则总数少于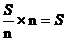 ,矛盾.
,矛盾.
假设都对于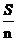 ,则总数多于
,则总数多于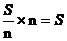 ,矛盾.
,矛盾.
从而命题得证.
形式二 把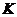 个元素任意分成
个元素任意分成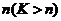 个集合,则一定有一个集合的元素个数不多于
个集合,则一定有一个集合的元素个数不多于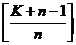 个,也一定有一个集合的元素个数不少于
个,也一定有一个集合的元素个数不少于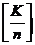 个.
个.
证明:(用反证法)设把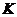 个元素分成
个元素分成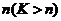 个集合,每个集合的元素都不多于
个集合,每个集合的元素都不多于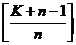 个,即少于
个,即少于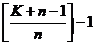 个,则这
个,则这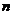 个集合元素总个数
个集合元素总个数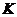 将有:
将有: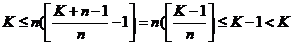 ,于题意矛盾,假设错误.
,于题意矛盾,假设错误.
同理,设每个集合的元素个数都多于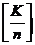 ,则至少有
,则至少有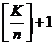 个,有:
个,有: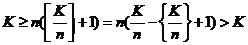 (
(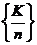 表示
表示 的小数部分),矛盾,假设错误.
的小数部分),矛盾,假设错误.
故命题得证.
形式三 把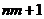 个元素任意分成
个元素任意分成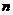 个集合
个集合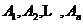 ,如果用
,如果用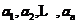 表示这
表示这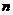 个集合里相应的元素个数,则一定存在某个
个集合里相应的元素个数,则一定存在某个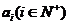 大于或等于
大于或等于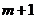 .
.
证明:不妨设结论错误,即每一个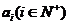 都有
都有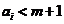 ,而
,而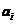 又是整数,所以有
又是整数,所以有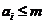 ,那么依次相加可得:
,那么依次相加可得: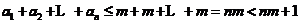 出现矛盾,假设有误,从而命题得证.
出现矛盾,假设有误,从而命题得证.
剩余内容已隐藏,请支付后下载全文,论文总字数:14362字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


