论文总字数:8192字
目 录
0.引言 3
1.问题的提出 3
2.预备知识 3
2.1外测度的定义与证明 3
2.2拓扑学预备知识补充 4
3.Riesz表示定理的具体内容 5
4.Riesz表示定理证明 5
4.1分别定义 和
和 5
5
4.2 的性质 6
的性质 6
4.3 的性质 9
的性质 9
4.4 =
= 的证明 12
的证明 12
4.5 和
和 在l上表示 12
在l上表示 12
4.6有关 的例子 12
的例子 12
5.结论 15
6.讨论 15
参考文献 16
致谢 17
Riesz表示定理的一个详细证明
李爽
,China
Abstract: In this paper, we use the notions of outer measure, local compact space, Hausdorff space and Urysohn’s lemma , etc, to give a proof of Riesz representation theorem in a more general form. In the proof, for a positive linear functional  , we introduce two measures
, we introduce two measures  and
and  , and prove Riesz representation theorem using the special properties of them. The Riesz representation theorem gives a very common way to construct measures with good properties.
, and prove Riesz representation theorem using the special properties of them. The Riesz representation theorem gives a very common way to construct measures with good properties.
This paper is divided into the following three parts: The first chapter is the definition and properties of outer measure, and Topological Preliminaries, the detailed content of Riesz representation theorem appears in Chapter2, in chapter3, we present the proof of Riesz representation theorem, and introduce the related counterexamples in special circumstances.
Key words: Riesz representation theorem , positive linear functional, outer regular, inner regular, Urysohn’s lemma.
0. 引言
Riesz表示定理是由匈牙利数学家Frigyes Riesz 在1909年提出的,苏联数学家Andrey Markov在1938年将结论扩展到了非复空间,在1941年日裔数学家Shizuo Kakutani扩展到复数Hausdorff空间。本文贡献利用了外测度,局部紧空间,Hausdorff空间,Urysohn’s 引理等,给Riesz表示定理一个更为广泛形式的详细证明,这个证明的特色是对一个正线性泛函 分别引入
分别引入 和
和 ,由这两个测度的种种特殊性质,逐渐从特殊到一般,详细证明这个定理。本文细分为以下几个部分:外测度的定义、性质与证明,拓扑学预备知识,Riesz表示定理的详细内容,及Riesz表示定理的证明过程,以及在特殊情况下的相关反例。
,由这两个测度的种种特殊性质,逐渐从特殊到一般,详细证明这个定理。本文细分为以下几个部分:外测度的定义、性质与证明,拓扑学预备知识,Riesz表示定理的详细内容,及Riesz表示定理的证明过程,以及在特殊情况下的相关反例。
问题的提出
Riesz表示定理是实分析的重要内容,它给出了一种非常一般的构造具有良好性质测度的方法。例如,从欧式空间上的黎曼积分出发,可自然定义 上的一个正线性泛函,由Riesz表示定理,其对应唯一一个Radon测度,事实上即为Lebesgue测度。这给出了引入Lebesgue测度的一个自然方法。
上的一个正线性泛函,由Riesz表示定理,其对应唯一一个Radon测度,事实上即为Lebesgue测度。这给出了引入Lebesgue测度的一个自然方法。
常见实分析教材如[1]等,对该定理的证明或缺乏关键细节,或较繁复。本文整理了一个Riesz表示定理的详细证明,将证明过程分解为一系列明显事实的组合。我们认为该证明将更加有利于对该定理的理解。
2. 预备知识
我们从文献[1]和文献[2]中,抽取出相关的测度论和拓扑学中一些定义和定理,为之后的证明做铺垫。
2.1外测度的定义与证明
定义1[1] :令 表示
表示 的所有子集(包括空集)所构成的集类,设
的所有子集(包括空集)所构成的集类,设 为
为 上的一非负集函数(约定
上的一非负集函数(约定 )。如果对任意子集
)。如果对任意子集 和
和 的一个可数覆盖
的一个可数覆盖 (即
(即 ),有
),有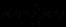 ,则称
,则称 为
为 上一外测度。
上一外测度。
上述定义中 的性质称做次
的性质称做次 可加性,一个简单推论是
可加性,一个简单推论是 具有单调性,即
具有单调性,即 。
。
定理1[1] :设 为
为 上的一外测度。令
上的一外测度。令

则 是一个
是一个 代数,且
代数,且 限于
限于 为一测度。我们称
为一测度。我们称 中元素为
中元素为 可测集。
可测集。
该定理的结论由以下几个命题组成。
命题1: ,
,
命题2[1] :如果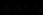 ,则
,则 
剩余内容已隐藏,请支付后下载全文,论文总字数:8192字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


