Landau-Kolmogorov不等式

论文总字数：5461字

目 录

1 引 言 1

2 技术性准备 1

3 实数域上的情况 2

4 半直线上的情况 3

5 区间上的情况 5

小 结 8

参考文献 8

致 谢 9

Landau-Kolmogorov不等式

滕笑涵

，China

Abstract：Landau proposed the interpolation inequality problem for the derivative of differentiable functions, which Kolmogorov investigated deeply. In this paper, we study the Landau-Kolmogorov type inequality for three cases: real axis, half real axis and intervals.

Keywords： Landau-Kolmogorov inequality, optimal constant，Taylor series

1.引言

不等式理论在数学中占有重要地位，而Landau不等式在函数逼近论和不等式理论中具有非常重要的作用。函数f的一阶导函数的范数一般不由f本身的范数控制，但可以由的范数共同控制。Landau在1913年着手研究这类不等式，他当时考虑的是若f是二次可微函数并且f,f"是有界的，，此处范数是上确界范数。对实轴上的函数最佳常数是，而半实轴上最佳常数是2。后来，数学家们又证明了更多情况和不同范数下的最佳常数。例如Littlewood 和Polya 研究了函数的范数的上述不等式，在实轴情形最佳常数为1；在半实轴情形最佳常数是。现如今，Landau不等式已经有了长足的发展，如Kallman和Rota建立了Banach空间上压缩半群的相应不等式。

该问题与数学分析、数值分析紧密结合，本文详细探讨了三种情形下的Landau-Kolmogorov不等式。

本文结构如下：第2章中，我们引入主要技术工具——积分型余项的Taylor公式；第3、4章在实轴，半实轴的情况下，我们分别证明了实轴，半实轴上的情况；最后一章对有限区间的情形，我们用分段方法证明该情况下的最佳常数。

2. 技术性准备

在数学分析中，已知，一般的带积分型余项的Taylor公式为

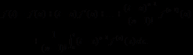
特别的，n=2时

（2.1）

在实数域上，令，根据Taylor公式(2.1)，我们得到

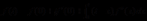（2.2)

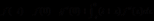(2.3)

两式相减，可得

（2.4）

3. 实数域上的情况

设F（x）是一个有2阶导数的有界函数，并且令

,，

我们希望找到之间的关系。

Landau定理：

即 (3.1)

为了证明Landau定理，实际上只需要考虑如下特殊情形

， (3.2)

让a和b为正常数，并且令,f仍为实轴上具有2阶导数的有界函数。

我们发现，从而（3.1）式等价于

我们从等式和中确定a和b并求出值

， (3.3)

Landau定理等价于如下：

定理：

如果

（3.4）

那么

（3.5）

证明：

根据(2.4)，我们得到

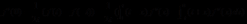
其中

放缩法可得

选择最优的t,即时 ，。

通过考虑函数的平移，易见对于一般的x上述不等式也成立，因此 。

为了证明（3.5）不等式是最优的，我们需找到函数使上述定理的等式成立

令

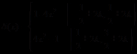k=0，1，2，……

满足特殊条件，并且。

定理： 如果满足条件（3.4），并且满足

那么，c为某一常数。

4. 半直线上的情况

我们定义，其中F 是定义在正半轴的函数。

关于半直线的问题与由第二节中Landau定理解决的问题相似，区别是现在只考虑定义在上的二阶可导函数。

Landau定理：如果 , ，，

那么 即.

与实轴情形类似，通过选择合适的正常数. 可以被调节使满足如下条件

剩余内容已隐藏，请支付后下载全文，论文总字数：5461字