论文总字数:8367字
目 录
1.预备知识.........................................................1
2.组合恒等式证明的常见方法....................................5
2.1公式法.........................................................5
2.2构造法.........................................................6
2.4母函数法.......................................................6
2.5递推关系法.....................................................7
2.6组合的意义.....................................................8
2.7概率法.........................................................8
2.8差分法.........................................................9
2.9复数方法.......................................................10
3.在其他领域的应用以及推广...........................10
3.1Euler恒等式....................................................10
3.2杨辉恒等式.....................................................12
3.3Sheehan组合恒等式.............................................12
3.4Cauchy组合恒等式..............................................13
4.致谢...............................................................14
5.参考文献..........................................................14
有关组合恒等式的研究
唐嘉悦
,China
Abstract: Modern mathematics is an active field in mathematics. Modern mathematics generally fall into two categories: 1 The object which is continuity. For example, mathematical analysis, the study of continuous equations and so on. 2 The object which is discrete. For example, combinatorial mathematics. Combinatorial mathemathics play an important role in basic mathematics research and it plays an important role in other fields. For example, enterprise financing, company managemant, transportation planning.
Combinatorial identity is an important part of combinatorial mathematics, The paper mainly intro duces the basic knowledge of combinatorial identities, concepts and some techniques and methords for solving combinatorial identities and its application in other aspects and related examples, Thus, the purpose of the study of combinatorial identities is achieved.
Keyword: method; combinatorial identity; probabilic method; the meaning of combination.
组合恒等式
1 预备知识
离散数学是现代数学的分支,是相对较独立的学科,最初并没有将其列入其他领域中,但是伴随着其他领域的发展,例如计算机,数论等,离散数学迅速发展,并与其他学科相互促进,相辅相成,对未来科学的发展起到了巨大的推动作用。
组合数定义
 :从
:从 个不同元素中选取
个不同元素中选取 个进行组合的数目。含有组合数的恒等式叫做组合恒等式。
个进行组合的数目。含有组合数的恒等式叫做组合恒等式。
 :从
:从 个不同的元素中选取
个不同的元素中选取 个元素进行有次序组合的个数。
个元素进行有次序组合的个数。
下面举出一些简单的组合恒等式以及推论并加以证明:
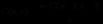 .
.
证明:式子 成立,同理可得
成立,同理可得  .
.
则将两式相除可得到 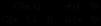 .
.
将上式整理得到  .
.
所以原式成立,得证。
 .
.
证明:式子 成立,将式子中
成立,将式子中 换成
换成 得到
得到 展开式,同理可得到
展开式,同理可得到 展开式,将四个式子综合可得
展开式,将四个式子综合可得
 .
.
-
 和
和 .
.
证明:这两个公式的证明方法相类似,运用二项式定理,将式子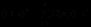 展开,当
展开,当 或
或 时,可以得到上述等式。
时,可以得到上述等式。
(4)  .
.
可将式子展开可得到结论。
说明:以上式子中, 为大于等于零的正整数。
为大于等于零的正整数。
a 推论一: .
.
证明:这个等式的证明我们可以直接将左边的式子与右边的式子分别展开,从右边推到左边或者从左边推到右边,得证。
也可以从两个角度理解,假设有 个苹果,我们想从中取出
个苹果,我们想从中取出 个,将其有顺序的排列,则有多少种方法?面对这个问题,我们有两种思路:
个,将其有顺序的排列,则有多少种方法?面对这个问题,我们有两种思路:
①从 个苹果中取出
个苹果中取出 个按顺序排列,一共有
个按顺序排列,一共有 种方法。
种方法。
②选择一个做标记的苹果,当选出的苹果中:(1)不包括做标记的苹果,则问题转化成从 个苹果中选出
个苹果中选出 个有顺序的排列,一共有
个有顺序的排列,一共有 种。(2)包括做标记的苹果,则问题转化成从
种。(2)包括做标记的苹果,则问题转化成从 个苹果中选出
个苹果中选出 个有顺序的排列,一共有
个有顺序的排列,一共有 种,再将做标记的苹果插入到
种,再将做标记的苹果插入到 个苹果中,共有
个苹果中,共有 种。
种。
综上所述: .
.
剩余内容已隐藏,请支付后下载全文,论文总字数:8367字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


