论文总字数：12527字

目 录

1 绪论 1

1.1研究斜路径湿延迟的意义 1

1.2 论文研究内容 1

1.2.1 NMF映射函数 2

1.2.2 维也纳函数（VMF） 2

1.2.3 全球投影函数（GMF） 3

2地基GPS水汽解算原理 4

2.1 大气可降水量PWV 4

2.2斜路径水汽SWV 5

2.3水汽层析 7

3数据 9

3.1数据来源 9

3.2 数据处理 11

4结果比较与分析 12

5总结 14

参考文献………………………………………………………………15

致谢……………………………………………………………………16

地基GPS斜路径湿延迟计算方法及实践

赵瀛坤

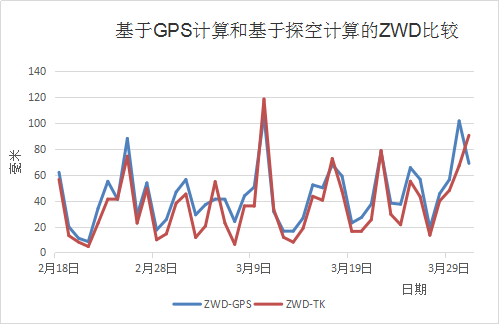
Abstract:The technology of ground-based GPS can be used to calculate with high precision.However,it is more important for us to know the four-dimensional distribution of the water vapour.Calculating SWD with precision plays a key role in water vapour tromography.The article is designed to introduce principles and methods of calculating PWV,SWV and water vapour tromography.Through comparing results,that Bias is 7,5687mm and RMS is 11.88720131mm, of ZWD calculationg in ground-based GPS and based on sounding,we can find that the technology of groud-based GPS can reach the same percision as the sounding.At the same time , the calculation of SWD came true based on NMF and the method of SWD.

Keywords:GPS;SWD;PWV;water vapour tromography.

1 绪论

1.1研究斜路径湿延迟的意义

在卫星全球导航定位中，星历误差在IGS(全球卫星定位服务局)的处理下控制在厘米级，所以轨道误差的的影响得到了很好的控制。除此之外，电离层与对流层对定位精度的影响也是颇为巨大的。由于GPS的信号采用双频传送，并且人们已经研究得出电离层延迟与信号频率平方成反比，电子数密度总量具体决定了大小，而双频改正可以极大程度弱化电离层对卫星信号的影响，使误差订正到毫米级，所以对流层的影响尤为重要了^[13]。建立大气模型是改正对流层延迟的主要方法，但是复杂的大气成分组成又使得精确的模型难以建立，所以不能精确修正对流层延迟已经成为一个亟待解决的阻碍GPS定位精度提高的重要因素。对流层的影响使得卫星型号的天顶延迟具有0.25m左右，而天顶延迟由湿延迟和干延迟(也称作静力延迟)。地面气象参数可以帮助高精度确定静力延迟到到0.5mm精度，这个精度已经非常高了。那么，研究如何高精度求解湿延迟对GPS定位就有着非凡的意义了。

此外，斜路径湿延迟在气象方面也有着非常重大的意义，它是利用地基GPS获取水汽在大气中的三维分布的必经之路。大量的实验证明了，地基GPS确实可以探测大气中的可降水量，并且达到可观的分辨率和精度，但是同时，实验可获取大气中的可降水量却无法提供水汽在大气中的垂直方向的信息。探空网也可以获取水汽的三维空间分布并供我们使用，然而探空站所获得的数据有着间距非常大，达到了百千米的量级，这样就很难得到范围较小更加精确的水汽分布。此外，水汽的三维分布也可以由气象卫星的资料反演获得，但是其误差非常大没有实际意义。那么，由地基GPS获取斜路径湿延迟计算出斜路径方向的水汽分布就成了求得水汽三维分布的重要途径了。因此，精确计算斜路径湿延迟在反演大气水汽含量过程中起决定性作用，能帮助研究人员准确的获取大气中的水汽分布，与水汽变化趋势，这对天气预报以及地球气候研究有着极其重大的意义。

1.2 论文研究内容

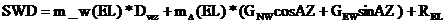（1）

斜路径湿延迟由上述公式进行计算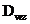，为天定湿延迟ZWD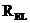，为单条斜路径残差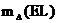，为梯度映射函数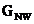，为南北方向湿梯度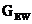，为东西方向湿梯度。由于条件限制无法得到其准确数据，本论文中的梯度映射函数与单条斜路径残差在此不做讨论，忽略不计。m_w（EL）所指即为湿映射函数。

1.2.1 NMF映射函数

Niell在1996年利用一个全球分布的无线电探空气球网的结果，研究做出了“全球大气延迟投影函数”，也就是NMF模型（1996Niell）^[11]。NMF模型与其他模型相比具有一些优点，它不仅比其他模型多加入了投影函数改正量，而且系数a，b，c是由测站的地理纬度、地理高度和年积日这些无需地面气象记录的数据所表示的函数。表达式为：

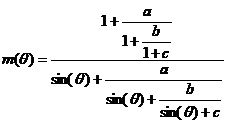(2)

（2）式中，θ是GPS卫星的高度角，平均值Aavg和幅值Aamp季节修正项组成了湿映射函数中的系数a，b，c，

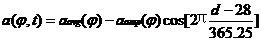(3)

（3）式中，是地理纬度，d日期在一年中的累积天数。Aavg，Aamp以及系数b，c这些数据是由Niell在1996年的论文中所给出的数据，经过线性内插再输入测站的地理纬度计算所得^[1]。

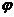
不过这个经验模型有着模拟过程简单的缺点，因为这个模型是一年中在北半球分布的电波资料的基础上得以建立的，只有纬度和季节会影响到这个模型的实践空间变量，再没有可以加以改正的其他客观数据。

1.2.2 维也纳函数（VMF）

2006年一种新的对流层映射函数模型维也纳映射函数模型被TechnischeUniversitätWien的J.Boehm提出，经过改进后成为常用的VMF1。这个函数模式是公认最精确最可靠的映射函数模型。它通过利用近几十年的ECMWF的观测数据资料重新确定了模型中系数b，c的值，而系数a干分量和湿分量中的值则是根据实测三十四小时延迟之后所生成的a的表数据，对其进行内插计算，获得可使用的值。网站mars.hg.tuwien.ac.at/~ecmwfl提供awet的格网列表文件的下载。

B_wet=0.00146 c_wet=0.04391，b_h=0.0029。干分量系数通过内插公式计算:

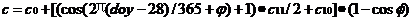(4)

1.2.3 全球投影函数（GMF）

1996年，Niell建立了投影函数NMF，但是随着该函数模型的发展，人们越来越明显的发现这个函数所产生的误差的大小仅仅对纬度变化敏感，但是却不会随着经度变化发生太大变化。所以人们在Niell函数的基础上对其进行改正完善，发展出了维也纳投影函数（VMF1），能够提供准确可靠的数据。但是源于NWM建立的投影函数无法在部分时间或测站备货区，并且VMF1模型在使用的时候会有三十多小时的时间延迟。Boehm J和Niell等人提出了一种新的基于NWM建立的全球投影函数（GMF）来克服VMF1带来的时延弊端。这个函数不仅与VMF1的一致性非常高，而且易于实现，输入参数也非常的简单，能够被全球使用。GMF是一种经验投影函数，它结算延迟量是利用了数值天气模型提供的全球对流层折射率，精度非常高，同时函数中的参数需要分析数据提供的湿度、气压和气温等基础信息，并加入了经度影响因素，是一个非常复杂的模型。GMF的形式依旧是三项连分式投影函数。

GMF湿分量投影函数为:

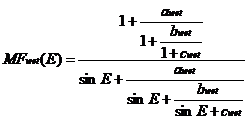(5)

式中，E为卫星高度角，b_wet=0.00146,c_wet=0.04391而系数a_wet则由下式确定：

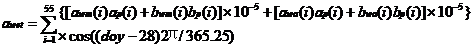(6)

系数a_wm，a_p，a_wa，b_wa，b_wm，b_p，均可在模型^[1]提供的表中查询得到。

2地基GPS水汽解算原理

斜路径湿延迟

映射函数

剩余内容已隐藏，请支付后下载全文，论文总字数：12527字

相关图片展示：