论文总字数：17582字

目 录

1 绪论 1

1.1 研究目的及意义 1

1.2 研究现状 1

1.2.1 国外现状 1

1.2.2 国内现状 2

1.3 研究内容 3

2 LS、TLS和LS-TLS方法研究介绍 3

2.1 常见的几种最小二乘法介绍及适用情况 3

2.1.1 经典最小二乘法 3

2.1.2 总体最小二乘法 4

2.1.3 递推最小二乘法 4

2.1.4 加权最小二乘法 4

2.2 奇异值分解法和常规总体最小二乘迭代解法 4

2.2.1 总体最小二乘法基本原理 4

2.2.2 奇异值分解法 5

2.2.3 常规迭代解法 6

2.3 混合总体最小二乘法 8

2.3.1 基本思想 8

2.3.2 求解思路 9

3 算法推导 11

3.1 间接平差原理 11

3.2 基于间接平差的新型总体最小二乘迭代解法 11

4 算例分析 16

4.1 算例1 16

4.2 算例2 17

5 总结与展望 17

参考文献 18

致谢 20

基于间接平差的新型总体最小二乘迭代解法

吴昌昊

, China

Abstract：This article introduces several common least squares methods and elaborated the basic principle of total least squares method and singular value decomposition and conventional iterative solutions. Due to the possible presence of constant columns in the coefficient matrix, however, some conventional singular value decomposition methods and the iterative solution is to correct all the elements in the coefficient matrix, this is inaccurate, so the mixed least squares method was used by people, but, the mixed total least squares method is tedious, and it has computational complexity and difficulty in programming. Therefore, this article introduces a new type of total least squares iterative solution based on indirect adjustment that is easier to solve, the purpose is to deal with the problem that the coefficient matrix may include constant columns while avoiding the complexity and difficulty of mixed total least squares method. Finally, by using examples to demonstrate its correctness.

Key words：Total Least Squares Iterative Solution; Singular Value Decomposition; Mixed Total Least Squares Method; Indirect Adjustment; Constant Column

1 绪论

研究目的及意义

为了提高参数估计精度和数据处理效率，我们可以（1）：采用高精度和高稳定性的测量仪器；（2）：改善观测条件；（3）：构造优化的数学模型。其中，高精度高稳定性的仪器条件受硬件条件的限制，成本大且研究周期较长；而较好的观测条件由人工干预，且只能产生比较有限的精度提高；而采取正当的数据处理办法，构造更优化的模型，相对于前两种，对测量技术领域具备重大意义。在最初的时候，我们对参数估值的求解一般都是在高斯—马尔科夫模型（G-M模型）的基础上使用最小二乘理论实现，在进行计算的时候不去考虑系数矩阵是否含有误差。但是，在进行具体的测绘数据处理实践的时候，我们发现，因为测量误差、人工误差和模型误差等状况的可能性，广泛存在着系数矩阵亦存在误差的状况，对于这种情况，研究学者们逐渐引入了总体最小二乘法（TLS）来处理这类问题，总体最小二乘法可以将系数矩阵A与观测向量L两者均存在误差的状况考虑在内^[1]，与普通最小二乘法的只考虑观测向量的误差状况相比较，是一种较为科学严谨的处理措施。

然而，在具体处理一些总体最小二乘问题的时候，我们发现，在系数矩阵A可能会有存在着无误差的常数列的状况，但常规的SVD法或者TLS迭代解法都不能将系数矩阵中含有常数列的问题考虑进去，同时却纠正了系数阵A中的全部元素，这是不准确也不严谨的。鉴于此，引入了LS-TLS算法，即混合总体最小二乘法^[2]，目的是为了处理系数矩阵A存在着常数列的情况，然而，我们认为混合总体最小二乘法是比较繁琐的，并且有计算量和编程难度较大的缺陷。针对于这种情况，在保证不降低精度的原则上，本文在间接平差的基础上，引出一种更容易解算的新型总体最小二乘迭代解法，目的是为了处理系数矩阵A中可能含有常数列的问题，同时规避混合总体最小二乘所带来的计算量繁琐缺陷，接着论证其正确性。

研究现状

1.2.1 国外现状

总体最小二乘法已有较长的历史，只是其思想和定义很晚才出现在文献中，在数理统计学中，这种方法称之为正交回归或变量误差。有关总体最小二乘方法的思想最早是由Adcock（1878）、Pearson（1901）、York(1966)等学者做的研究，但都仅仅被当做是一个具有一般性的最小二乘问题来解算，当时主要讨论的是正交回归的方法问题和线性方程的近似计算方法。直到20世纪90年代初，第一个数值稳定解法被Golub等提出，即著名的的奇异值分解法（SVD）^[3]，并且用数值的观念第一次对这种解算方式进行了深入的剖析，总体最小二乘法的命名由此诞生。接着经历了不同学科领域理论的发展与完善，直到再由VanHuffel等 对总体最小二乘法进行了全面的钻研讨论^[4,5]，并经过测绘学者的不断钻研，被广泛的用来进行数据处理，于2015年相关研究达到最热。

在数学方面，经过20多年的研究，总体最小二乘问题主要在研究解的性能、充分条件、与经典最小二乘解之间的关系、算法的实现、总体最小二乘问题的误差理论、总体最小二乘迭代算法问题以及加权总体最小二乘的相关性质等方面^[2]的情况。在近几年时间里，总体最小二乘方法在测绘学科中的理论研究和应用研究开始广泛地展开，并逐渐被重视。自误差变量模型中附加约束条件的解算公式由国外俄亥俄州立大学给出之后，便开始了对总体最小二乘理论研究方面的研究。Schaffrin^[6,7]教授在随后的几年里进行了深入研究，连续发表了几篇文章阐述并说明了有关总体最小二乘问题的解算算法的问题。并就TLS的加权解算算法和迭代解法以及多元线性误差变量模型的相关性质等作了一系列的讨论，并将其应用到了直线拟合与坐标转换的问题上，相比于经典最小二乘法，提高了测绘数据求解解算的科学性和有效性。

1.2.2 国内现状

总体最小二乘法经过测绘学者的不断研究，广泛的被用来进行处理数据，是一个探讨热门，而在我国测绘学科领域，学者丁克良^[8]等研究了基于QR分解的总体最小二乘方法，并且以曲线拟合作为实例运用验证总体最小二乘法，证实了同时考虑自变量与因变量误差的合理性^[9]；鲁铁定^[2]等对此方法进行了进一步研究，给出了不只顾及自变量还要顾及因变量的计算模型并将其应用到一元线性回归模型的解算；陆珏和陈义^[10]等将总体最小二乘法应用到空间后方交会外方位元素的解算中，与经典最小二乘方法对比得到了更为准确严密的结果，在算法方面应用了由Golub等给出的SVD法^[3]；陆珏和陈义^[9]等通过实现总体最小二乘法在三维小角度空间直角坐标转换中的应用体现了总体最小二乘法相比于经典最小二乘法的优势，在算法上采用的是Van Huffel和Vandewalle等提出的基于矩阵分析应用的奇异值^[2]分解法；王乐洋等将总体最小二乘法应用于求解应变参数问题，同时和鲁铁定及周世建^[11]一起研究推导出了混合总体最小二乘的迭代解算算法；鲁铁定和周世建^[12]比较了TLS迭代解法和SVD法的关系，证明了TLS的迭代算法和SVD法的结果具有一致性；鲁铁定和陶本藻^[13]讨论研究了基于线性回归的TLS算法，证明通过TLS算法，纠正系数矩阵所含有的误差^[14]，能够解决处理经典最小二乘法在y = ax b与x = a’y b’所拟合出的结果是不相同的状况；余岸竹^[15]将TLS法应用在基于线阵卫星遥感影像的光束法平差解算中，并把外方位元素构造成虚拟观测方程，从而进行求解。

在测绘学科方面目前所应用的总体最小二乘采用的方法基本上都是通过在数学中的理论所总结出的解算方法，前提条件都是以观测值向量和系数矩阵为独立等精度进行运算情形下的应用^[2]，所以总体最小二乘方法的理论体系并不完备，同时，在测绘科学领域，系数矩阵A中可能会有含有常数列的状况，并且常规SVD法和一般的TLS迭代解法都是纠正了系数矩阵A中的全部元素，却没有去考虑系数矩阵中哪部分是误差列和哪部分是常数列的状况，这可能会导致解算结果偏差很大，作为测绘科学专业的大学优秀本科生应努力学习新的知识，研究新的方法和降低计算难度，提高数据精度，使其成为测绘测量平差方法的一部分，从而提高测绘数据的严谨性和效率。

研究内容

在测绘领域，系数矩阵A与观测向量L同时存在误差的情况是广泛存在的，适合采用总体最小二乘法处理的问题有很多，如：高程拟合、线性回归等。然而，在具体处理数据的时候，我们会发现，系数矩阵A中可能会存在着含有常数列的状况，并且常规SVD法和TLS迭代解法都不能分离系数矩阵中含有的常数列，却纠正了全部元素，这是不严谨且不准确的。

本文简要介绍了几种最小二乘法的类型，接着引入了总体最小二乘法的原理和求解解算方法，并突出了总体最小二乘法相对于普通最小二乘的优越性。总体最小二乘问题的解算措施有奇异值分解和迭代算法，然后论述了TLS奇异值分解和TLS迭代解法的过程，并且指出它们虽然可以考虑并纠正系数矩阵中含有的误差，但没有去考虑系数矩阵中哪部分是误差列和哪部分是常数列的状况，而是进行全部纠正，这是不准确的，甚至会导致数据误差很大的后果。考虑到系数矩阵中可能会含有常数列的问题，于是引入并阐述了混合^[1]总体最小二乘法（LS-TLS），并论述了它的基本思想和求解思路以及算法过程，然而，通过算法过程，我们发现，混合总体最小二乘法的繁琐复杂带给了人们很多困扰，针对于这种情况，在保证不降低精度的原则上，本文在间接平差的基础上，基于matlab的程序实现，引出一种更容易解算的新型总体最小二乘迭代解法，目的是为了处理系数矩阵A中可能会含有常数列的情况，同时规避混合总体最小二乘法所带来的繁琐复杂问题以及常规SVD法和TLS迭代解法的缺陷问题，使测量数据能够更加的准确和严密，使用方便，然后由算例分析来论证其正确性和严谨性。

2 LS、TLS和LS-TLS方法研究介绍

2.1 常见的几种最小二乘法介绍及适用情况

2.1.1 经典最小二乘法

最小二乘法（LS），寻求“最佳”的参数估值。然而，它只能保证一个方向的误差最小，比如对于平面直线拟合来说，y = ax b与x = a’y b’所拟合出的结果是不一样的，因此，该方法一般只应用在解决观测向量存在误差而系数矩阵不存在误差的问题。

2.1.2 总体最小二乘法

我们通过具体的测量数据处理发现，因为测量误差、人工误差和模型误差等状况的可能性，我们发现，广泛存在着系数矩阵亦存在着误差的状况，则我们列出总体最小二乘法的函数模型^[2] ( A E _A ) X = L V，其中：系数矩阵A∈R^m×n，系数矩阵A的误差矩阵E_A ∈R^m×n，未知参数向量X∈R^n×1，观测向量L∈R^m×1，观测向量L的真误差V∈R^m×1，，且有，系数矩阵A的秩为 n 且小于m。针对上述情况，一般当系数矩阵A和观测向量L均存在误差的时候被采用。

2.1.3 递推最小二乘法

在辨识系统运行时，利用新引入的观测数据，在得到每个新的观测数据后，再根据先前估计的结果进行估计。根据递推算法，得到了参数估计。随着新观测数据的不断获取，参数估计不断得到，直到参数估计符合标准则停止递推。即新计算得到的估计值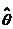（k）= 上一次的估计值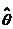（k —1） 改正数^[16]。

2.1.4 加权最小二乘法

当最小二乘函数模型被证明含有异方差性时，这时候就应该采取新方法来估计平差模型，此时，我们一般去运用加权最小二乘法来处理这类状况，它旨在处理估计原模型，让其转化到没有异方差性的函数模型，接着运用经典最小二乘法来进行参数的估计。

剩余内容已隐藏，请支付后下载全文，论文总字数：17582字