论文总字数:33975字
目 录
一、绪论 1
1.1GNSS数据预报预测意义和目的 1
1.2 GNSS变形监测数据预报国内外研究现状 1
1.3本文主要内容 2
二、GNSS数据预报算法模型 3
2.1卡尔曼滤波 3
2.2方差补偿自适应卡尔曼滤波 5
2.3基于极大验后估计自适应卡尔曼滤波 6
2.4基于方差分量估计原理的自适应卡尔曼滤波 8
三、卡尔曼滤波在实际中的应用 10
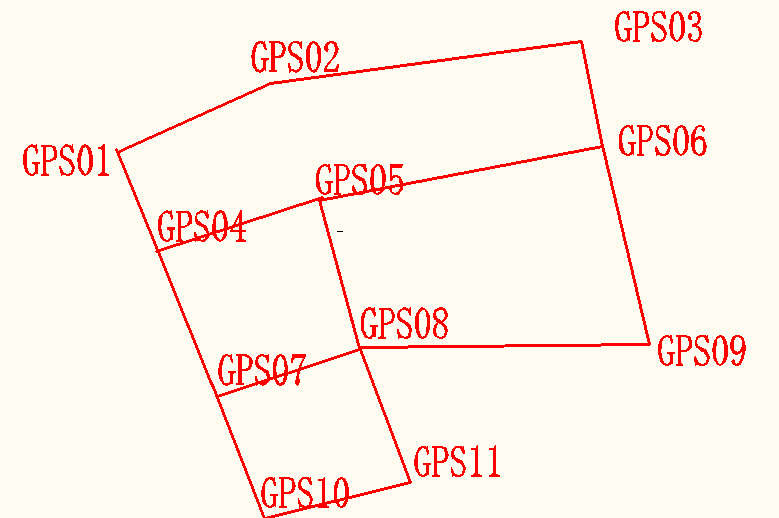
3.1GNSS变形监测在泥石流滑坡中的应用 10
3.2卡尔曼滤波在滑坡数据处理中的应用 11
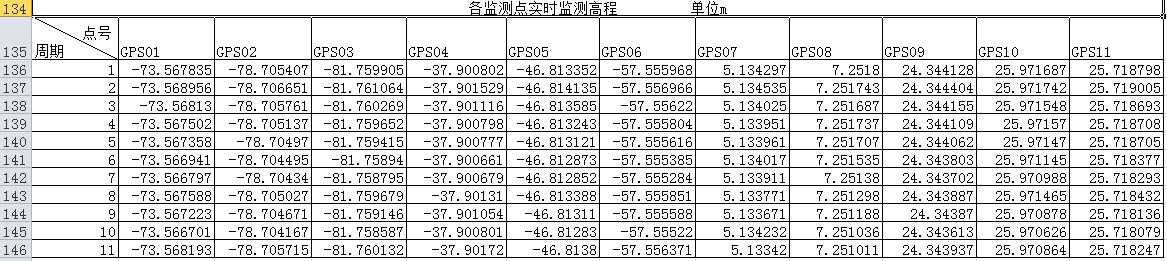
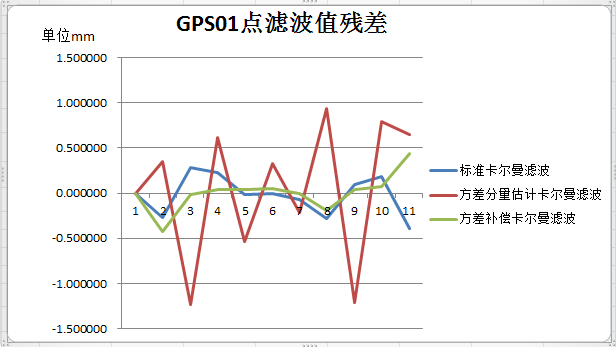
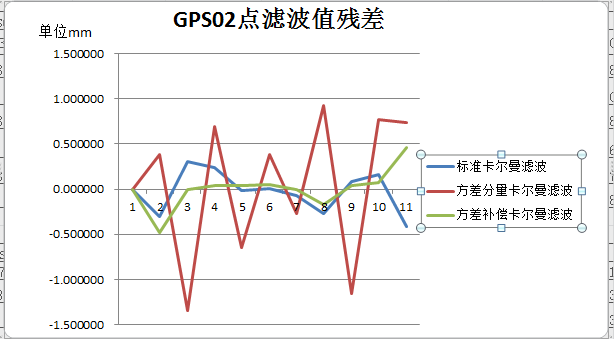
3.2.1 三种卡尔曼滤波模型数据处理对比 11
3.2.2数据结果分析 23
3.3自适应卡尔曼滤波模型建立及应用 23
3.3.1数学模型建立步骤 23
3.3.2模型流程图 25
3.3.3数据预测处理 25
四、其他滑坡影响因子 27
4.1降雨因子 27
4.2水位因子 33
五、总结 34
5.1小结 34
5.2论文的不足 34
参考文献 35
致谢 36
基于GNSS数据的变形监测预报研究
秦臻
,China
Abstract: This paper mainly introduces the application of GNSS in practice, and uses the corresponding algorithm model to process and analyze GNSS data, so as to predict the variation trend of deformation variants. The article uses the standard Kalman filter, and on its basis improved variance component adaptive Kalman filter and variance compensation adaptive Kalman filter. Using the above methods, the measured data are processed separately, and the data processing results are analyzed to finally use the optimal model for further forecasting. The optimal model still has many deficiencies in data analysis, but its accuracy meets the forecasting requirements. Deformation monitoring for deformable bodies should select the most effective model for real-time analysis and predict change trends, so that the deformation monitoring system is more complete. The article analyzes the measured data of the GNSS and finds that the Kalman filter can eliminate the noise in the data and obtain a more accurate filter value. The adaptive Kalman filter with variance compensation should be able to predict the deformation monitoring data in real time. The difference between the three model filtering values and the actual value can be within 1mm, and the difference between the predicted value and the actual value is less than 1cm to meet the deformation monitoring system in real time.
Key words: GNSS; Kalman filter; deformation monitoring ; estimating variance component; variance compensation.
一、绪论
1.1GNSS数据预报预测意义和目的
在世界各地经常有各种灾害发生,例如山体滑坡、泥石流、建筑物坍塌等现象。这些灾害不仅会造成国家和个人的财产损失甚至经常有人因此失去宝贵的生命。1970年秘鲁发生泥石流造成大量人员死亡,1988年意大利南部受到泥石流冲击超过100人遇难,2000多人人失去了家园。中国也有过很多泥石流灾害造成了很大程度损失,如2010年甘肃舟曲发生特大泥石流,1434人遇难整个舟曲被夷为平地;同年四川省又发生多起泥石流灾害造成了交通瘫痪,百姓家园被毁损失惨重。2005年广州珠海某处广场坍塌,2009年上海某楼盘倒塌,2012年哈尔滨阳明滩大桥垮塌,这些事故无一例外对经济以及社会安全感造成巨大影响。
为了能最大程度上减少伤亡和财产损失提前的防范意识就显得尤为重要。所以我们要在灾害发生之前做出及时的预报,GNSS变形监测就是一种很好的预防监测手段,它已经在许多工程当中大量使用,它可以通过实时对形变体监测第一时间掌握动态信息,并对未来变化趋势做出及时判断预测,做好防范措施将可能发生的灾害损失降到最低。GNSS技术由中国的北斗、美国的GPS俄罗斯的GLONASS和欧洲的伽利略卫星导航系统组成。随着技术的进步它具有全天候,全时域的优点,无需在站点之间查看,定位精度高,不仅如此还可以同时确定三维坐标子系统的点位。
GNSS变形监测是一个系统的过程,从一开始布设监测点到后来获取数据,并对数据处理分析之后对系统变化做出相应的预测。在这其中数据处理就显得尤为重要,只有正确处理分析数据才能反应变形的基本情况。当前的主要目的是利用观测数据计算出相应的模型参数,对已知模型进行合理选择和适当修改之后建立完善的监测预报体系。
1.2 GNSS变形监测数据预报国内外研究现状
分析变形监测数据并描述变形状态包括常规分析和数学模型分析。常规分析的方法可以通过用监测点的坐标计算倾斜,旋转,扭曲,弯曲度等来认识建筑物和结构的稳定性,或者通过建筑方式了解变形趋势和比较方法。通常用数学模型分析方法包含统计分析,时间序列分析,灰色理论等对变形监测数据进行系统分析。由于变形监测数据不可避免地受到各种噪声干扰,观测数据通常受到污染。为了提高监测数据的准确性和可靠性,首先要求对变形数据序列进行误差分析。小波分析和卡尔曼滤波分别在工程实践中具有很高的应用价值,在国内外被广泛应用于降低噪声。小波分析和卡尔曼滤波方法对实测的变形数据进行分析,对监测数据序列进行去噪,得到监测点的变形趋势。其中卡尔曼滤波广泛应用于各行业中,例如空间轨道修正机器人系统控制、导弹追踪等领域。近年来在当下热门领域研究中卡尔曼滤波也发挥着不可或缺的作用,其在组合导航与动态定位、微观经济学、传感数据融合、图像分割、图像边缘监测等方面占有重要地位。卡尔曼滤波是一种动态数据处理方法,能够快速有效处理大量变形监测动态数据,实时对未知模型参数和噪声统计特性进行适当估计和修正。且能有效改善实测数据精度。
1.3本文主要内容
(1)文章介绍了GNSS变形监测的现状,意义和特点。 同时对GNSS变形监测误差分析、数据处理步骤和监测手段等方面的发展现状和趋势加以总结。
(2)详细描述了标准卡尔曼滤波、方差补偿卡尔曼滤波,改进后的基于方差分量卡尔曼滤波,基于极大验后卡尔曼滤波的模型和理论方法。目的是更好地处理GNSS变形监测数据,并提高处理后数据的准确性和稳定性。
(3)介绍了卡尔曼滤波在重庆奉节县某新滑坡应急专业监测中的应用。首先,处理和分析该地变形监测数据,验证了卡尔曼滤波的可行性。 其次通过对几种方法的比较选择最优的一种方法建立模型。 最后通过该方法再对GNSS监测数据进行预测,对预测后的数据进行分析验证其精确程度并得出结论。
二、GNSS数据预报算法模型
目前,处理形变监测数据的各种实用方法有很多,已广泛应用于各个领域如地安全监测分析、健康诊断等。 在诸多方法中卡尔曼滤波也是一种较精确且使用广泛的数据处理方法。 标准卡尔曼滤波将参数计算与预测结合起来,可以实时反映运动目标的状态。 然而,它也有自身存在的一些弊端,比如初始值选择的难度以及在某些条件下估计值的不可靠性。 因此,自适应卡尔曼滤波修改了不确定或未知模型的参数和噪声统计特性,以减少模型误差的影响,使结果更靠近真实值。
2.1卡尔曼滤波
变形监测系统建立的卡尔曼滤波模型首先包括状态方程和观测方程。 针对于对于线性系统而言,离散形式的表达式如下所示:
状态方程: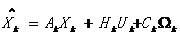 (2-1)
(2-1)
观测方程为: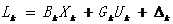 (2-2)
(2-2)
式中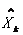 是在 k 时刻系统的 n×1 维的最佳滤波值,为在k时刻系统的 n × n维的状态向量系数矩阵,是在 k 时刻n × 1 维的系统状态向量,是在 k 时刻系统 n×n 维的控制向量系数矩阵,是在 k 时刻n×1 维的系统控制向量,是在 k 时刻系统n×r 维的动态噪音向量系数矩阵,
是在 k 时刻系统的 n×1 维的最佳滤波值,为在k时刻系统的 n × n维的状态向量系数矩阵,是在 k 时刻n × 1 维的系统状态向量,是在 k 时刻系统 n×n 维的控制向量系数矩阵,是在 k 时刻n×1 维的系统控制向量,是在 k 时刻系统n×r 维的动态噪音向量系数矩阵,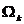 是在 k 时刻系统 r×1 维的动态噪声向量,
是在 k 时刻系统 r×1 维的动态噪声向量, 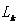 是在 k 时刻的m×1维的系统观测向量,
是在 k 时刻的m×1维的系统观测向量,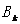 是在k 时刻m × n维的系统状态向量系数矩阵,
是在k 时刻m × n维的系统状态向量系数矩阵,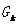 是在 k 时刻 的n×1 维的系统控制向量系数矩阵,
是在 k 时刻 的n×1 维的系统控制向量系数矩阵,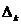 是k时刻 m×1 维的系统观测噪声向量。上式(2-1)和(2-2)就为卡尔曼滤波的数学模型。
是k时刻 m×1 维的系统观测噪声向量。上式(2-1)和(2-2)就为卡尔曼滤波的数学模型。
对于变形监测系统,我们不考虑确定性输入,也就是说,控制矢量为零。则 (2-3)
剩余内容已隐藏,请支付后下载全文,论文总字数:33975字
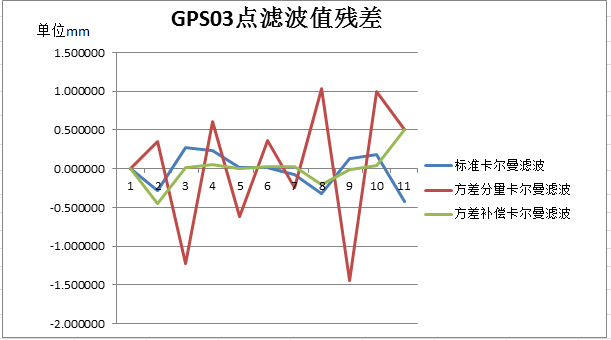
相关图片展示:
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


