论文总字数：22199字

摘 要

SIFT是计算机视觉中常用的特征提取算法，它从图像子区域中提取有用的特征并表示成一个向量，称为描述子（descriptor），实际中常用Dense-SIFT, 即从图像中提取大量的描述子。Dense-SIFT对图像的很多几何变化具有很强的不变性，但缺点是计算复杂度高，实时性较差。

本文基于GPU并行计算对Dense-SIFT算法进行加速。首先对程序进行性能分析，将程序分为若干独立模块，统计各模块的执行时间，找出耗时较多的模块。接着重点分析该模块算法结构，提出算法并行化方案，包括优化线程结构避免线程阻塞、优化存储器使用提高带宽使用率，以及一些程序实现上的优化。然后，采用NVIDIA推出的CUDA C语言实现并行程序，并在 PASCAL VOC 2007 数据集上进行测试。通过比较GPU并行程序与传统C 程序性能，验证了GPU并行计算对Dense-SIFT速度的提升。对于640 * 480的图像，GPU并行程序比传统C 程序快5.8倍。

关键词：并行计算；GPU；CUDA；Dense-SIFT；特征提取

Accelerate Dense-SIFT with GPU parallel computing

SIFT is a common algorithm to extract features from image. It get useful features from a subarea of the image to form a vector, which is called a descriptor. For practical reasons, Dense-SIFT is more often used to extract large amount of descriptors. Dense-SIFT is highly invariant to image rotation, scaling, and perspective. However, this algorithm is complex and cannot be applied for real-time calculation.

This thesis is to accelerate Dense-SIFT based on GPU parallel calculation. We first analysis the performance of the program (C version, implement by VLFeat) by dividing the whole program into several separate parts, timing each of them and then finding out the time-consuming ones. Then we emphasize on the structure of this program and propose a new parallel scheme, including optimizing block size to avoid idle thread, and optimizing the implement of the program. We realize this parallel structure on NVIDIA CUDA and test it on PASCAL VOC 2007 dataset. By the comparison of the new parallel structure and conventional C program, it can be proved that the new GPU parallel calculation can accelerate the Dense-SIFT. For a picture of 640*480, the speed of GPU parallel calculation is 5.8 times faster than the conventional methods.

目录

第一章 绪 论 4

1.1 引言 4

1.2 SIFT特征提取 4

1.2.1 构建高斯金字塔 4

1.2.2 尺度空间极值 5

1.2.3 剔除极值响应较弱的点 6

1.2.4 去除边缘效应 6

1.2.5 极值点的方向分配 7

1.2.6 计算描述子 7

1.3 Dense SIFT 8

1.4 VLFeat开源项目 9

1.5 GPU并行计算。 9

1.5.1 GPU vs GPU 10

1.5.2 GPGPU技术 10

1.5.3 CUDA 10

1.5.4 计算能力 11

1.5.5 CUDA线程结构 11

1.5.6 GPU存储器结构 11

第二章 CUDA加速Dense SIFT特征提取 13

2.1 CUDA性能测试 13

2.1.1 opencv CUDA模块 13

2.1.2 CUDA测试-Hough变换 13

2.2 Dense SIFT算法性能分析 13

2.3 CUDA C程序结构 14

2.4 Dense SIFT并行加速 15

2.5 使用共享存储器优化 16

2.6 避免线程空闲 17

2.7 分离二维卷积 18

2.8 GPU存储器优化 18

2.8.1内存对齐概念 18

第三章 优化程序实现 20

3.1 循环展开 20

3.2 描述子归一化优化方案 20

3.2.1 归一化处理 20

3.2.2 浮点数快速开平方 21

3.3 openMP加速描述子处理 23

第四章 实验结果 24

4.1 实验环境 24

4.2 实验结论 24

参考文献 26

致谢 27

第一章 绪 论

• 1. 引言

特征提取是机器学习过程中最重要的步骤之一，好的特征可以在保留原始数据绝大部分信息的同时减少冗余数据，降低模型训练和预测的计算量。

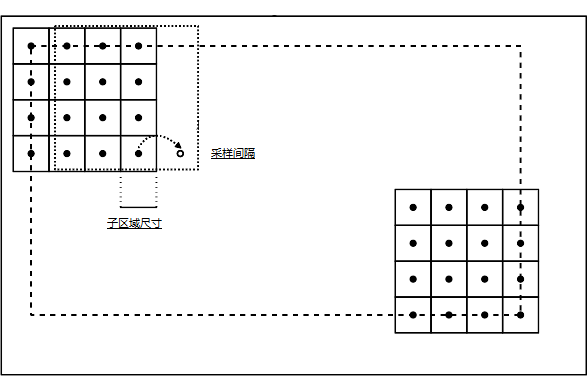
计算机视觉中有许多常用的特征描述，简单的如梯度信息、边缘信息。而Scale-Invariant Feature Transform (SIFT)特征描述是最常用的特征描述方式之一，它包括特征检测和特征提取两个部分，检测是从其中发现“有用、重要”的部分(特征点)， 提取是当给定一个图像区域，比如一个16x16的 子图像，从这个图像区域中提取有用的特征表示成一个向量，称为这个图像区域的描述子。

在计算机视觉中，常用dense sift descriptor, 也就是从图像中提取很多这样的描述子。但描述效果提升的同时带来的是计算量的提升，SIFT特征提取本身就有实时性差的缺点，dense sift descriptor对于分辨率较高的图像较难在短时间内得到结果，而现在前沿的机器学习算法都需要在大量的训练数据上进行计算，一些著名的公开数据集，如PASCAL VOC 2007 dataset^[10] 仅训练数据就包含5011张各类场景的图片，而2012年由华人教授李菲菲发起的图像数据项目ImageNet^[11]至今为止已经有一千四百多万张图片，在这么大的数据上直接应用dense sift descriptor需要大量的计算时间。

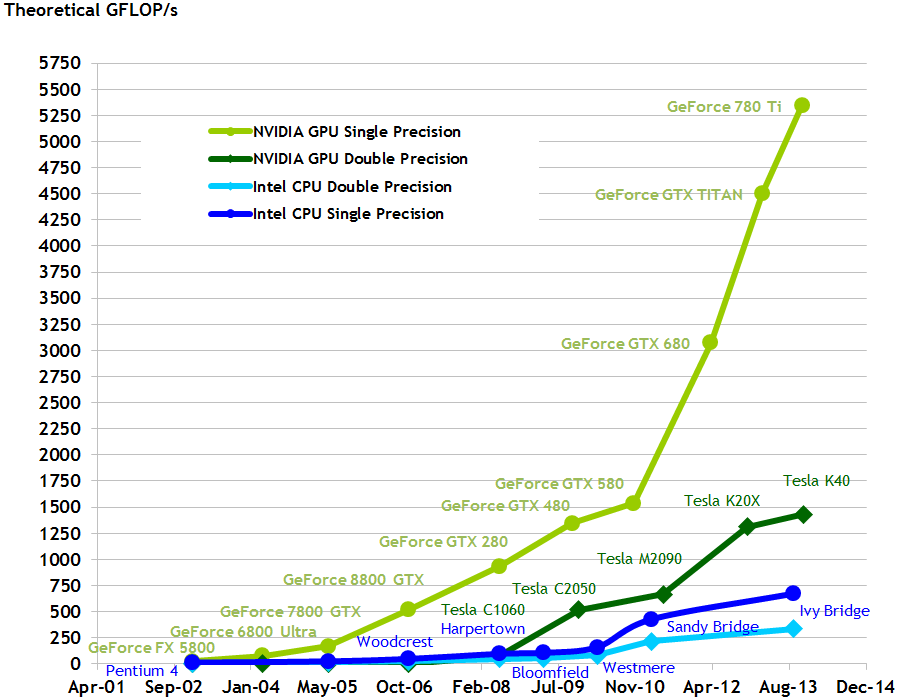
GPU计算是利用图像处理单元（GPU）结合CPU来加速科学计算。由NVIDIA公司于2007年首创，至今为止已经在各研究所、大学获得了广泛的应用。GPU计算将应用程序或算法中计算密集型的部分在GPU上实现，而其他部分仍在CPU上实现，使得计算速度有了显著性的提升。可以比较CPU和GPU的工作原理来理解这一结果:CPU包含较少的核心数，主要为了执行串行的控制代码，而GPU则因为需要同时处理多个任务而被设计成具有多个核心数（可能上千个）的结构，尽管每个核心数的计算能力CPU远胜GPU。

2006年11月，NVIDIA推出了通用并行计算平台CUDA，在对应的软件平台上，用户可以使用和C十分相似的高级语言进行编程，极大的方便了算法在GPU平台上的实现。CUDA C语言允许用户像C语言一样定义一个kernel函数，不同的是，CUDA C的kernel函数可以在GPU上并行的执行，用户可以自己定义所需要的线程数量。CUDA中线程的概念与操作系统中线程的概念并不一样，操作系统中不同的线程仅仅是进行快速的切换，而非真正意义上的并行。而CUDA中的线程是同时运行于不同核上面的，是真正意义上的并行计算。

• 1. SIFT特征提取

SIFT即Scale-invariant feature transform（尺度不变特征转换），由David Lowe于2004年整理完善后发表。SIFT特征提取主要分为以下4个步骤：

1. 构建高斯金字塔。
2. 极值检测、关键点定位。
3. 确定关键点方向。
4. 计算描述子。

具体的计算过程如下：

• • 1. 构建高斯金字塔

为了实现旋转不变性和高效率，我们在尺度空间的最大值和最小值中寻找关键点，这个过程可以通过建立图像金字塔非常有效的进行。高斯金字塔指的是，将原图像进行高斯模糊并隔点采样。重复多次会得到一系列大小不一的图像，由大到小组成一个塔状模型，原图像为模型的第一层。

为了让尺度空间连续，高斯金字塔在降采样的基础上加了高斯滤波。将高斯金字塔每层的图像使用不同参数做高斯模糊，这样每层会包含多张模糊图像，将金字塔每层多张图像称为一组（Octave）。金字塔每层包含一组图像，组数与层数相同。

图1. 高斯金字塔

在实际使用中，常用高斯差分金字塔（Difference of Gaussian， DOG），即将高斯金字塔每组中上下两层图像相减。

图2.

• • 1. 尺度空间极值

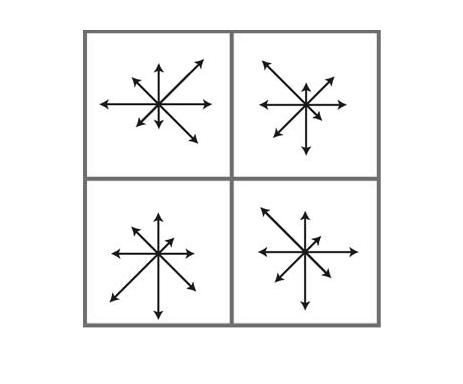
在DOG空间中搜索极值点，作为候选的关键点。为了寻找DoG空间的极值点，每一个像素点要和它周围的所有点比较，即同尺度的8个点、相邻尺度图层的18个点共26个点（如图三所示）。由于噪声的影响和DoG算子的边缘响应，找到的极值点并不全部是稳定的特征点，需要进一步剔除极值响应较弱的点并消除边缘响应。

图3. 尺度空间极值检测

• • 1. 剔除极值响应较弱的点

Lowe与Brown^[1]提出拟合三维二次方程的方法，将该方法使用到尺度空间函数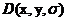的泰勒展开式，即:

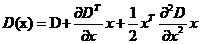
在采样点处计算D(x)和D(x)的导数， 其中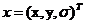是距离采样点的偏移，对上式求导数并使之为0，得到局部极值点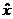，即：

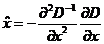
将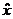 代入D(x)，若 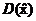小于一定的阈值，则认为 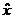处极值响应较弱，可以剔除。在Lowe的论文中^[2]，若 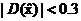，则将该点剔除。

• • 1. 去除边缘效应

高斯差分模型有较强的边缘响应，需要去除不稳定的边缘点。在高斯差分模型中，主曲率在边缘处较大，而在垂直边缘的方向较小，因此可以利用这一性质去除边缘响应^[2]。

首先通过计算极值点的Hessian矩阵来计算主曲率:

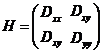
令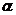 表示H较大的特征值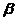，表示H较小的特征值，则：

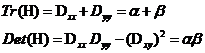
令r为两个特征值的比，即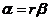 ，可以得到式：

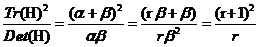
剩余内容已隐藏，请支付后下载全文，论文总字数：22199字

相关图片展示：