论文总字数：18503字

目 录

1.绪论 1

1.1 研究背景及意义 1

1.2 国内外研究现状 1

1.3 本文主要研究内容 2

2.图像压缩编码 3

2.1 图像压缩的信息度量和数据冗余 3

2.2 图像压缩编码方法 4

2.3 图像压缩技术的性能指标 4

3.经验模态分解的算法和实现 5

3.1 经验模态分解（EMD）方法 5

3.1.1 EMD方法的原理 5

3.1.2 一维经验模态分解算法和实现 7

3.2 二维经验模态分解（BEMD）方法 9

3.2.1 BEMD方法的步骤 9

3.2.2 BEMD分解过程中的关键 12

3.3 本章小结 13

4.基于BEMD方法的图像压缩 14

4.1 基于BEMD方法的极值点压缩 14

4.2 基于BEMD方法的DCT压缩分析 15

4.3 基于BEMD方法的哈夫曼压缩分析 17

5.总结与展望 19

参考文献 20

致谢 22

基于EMD方法的图像压缩研究

张思绮

, China

Abstract: Empirical mode decomposition method is a new non-stationary signal analysis method proposed by Huang, The EMD method decomposes a complex signal into a stack of multiple intrinsic modal functions and residual residuals. The two-dimensional empirical mode decomposition method is an extension of the EMD method in the field of two-dimensional imaging. It is a new multi-scale signal analysis method. Its development and development are still short, and the specific research is not mature enough. In recent years, the BEMD method has been gradually applied in the fields of image fusion, image denoising, etc., but less research has been done on image compression. This article briefly introduced the basic knowledge of image compression coding, briefly introduced the existing image compression methods and image compression technology performance indicators; elaborated the basic theory of EMD method and BEMD method, and focused on the three major issues in the BEMD method. The key point uses a suitable method to complete the simulation of the signal. This paper studies three kinds of image compression methods based on BEMD. The extremum point compression based on BEMD shortens the stream length to some extent, but from the viewpoint of subjective visual and objective data, the reconstructed image quality obtained is not high. BEMD-based DCT compression and BEMD-based Huffman compression have achieved good results. From the perspective of subjective vision and objective data, it is a feasible compression method.

Keywords: Empirical Mode Decomposition; Intrinsic Mode Function;BEMD; Image Compression

1.绪论

1.1 研究背景及意义

随着科技的快速发展，各项通信网络、计算机技术的大面积的应用，我们的社会已经进入了瞬息万变的数字化信息的时代。在现代化、信息化的今天，准确、即时、高效地获得各类尽可能多的有效信息已经成为社会各界的迫切需求。而其信息主要的内容——图像信息，有着容易识别、内容丰富、直观可辨等优点，因而被广泛应用，在社会各界尤其是科技和经济的领域发挥着重要的作用。所以，数字图像信息的相关处理、存储办法和传输在人类社会生活的作用愈加突出，大家对接受图像信息的各方面要求也愈加迫切。

但是，数字图像信息占有的字节多，信息量大。这需要计算机有着相当高的处理和存储数据的能力，并且，如此大的信息量也会使图像的信道传输速度减慢。所以，为了可以在便捷地对图像进行处理、存储和传输的同时减少图像的数据传输量，提高速度，往往需要对图像进行压缩，要求既保证图像质量，也能获得高的压缩比。如果图像压缩技术停滞不前，那么大容量的图像存储和传输将会很难实现，各项新技术的发展与应用也会受到很大的阻力，科学信息技术的发展也会因此受到限制。

小波变换、维格纳瑞利分布和傅立叶变换都是目前有的用来信号时频分析的方法^[1]。他们将信号分解成一系列各自的方法定义的基本函数。EMD方法在信号处理方面有着很大的优势，尤其体现在二维信号的处理上。它可以把非平稳、非线性的信号，根据其自身的局部特征，自适应地分解成为频率由高至低的、局部窄带的各个分量的固有模态函数（IMF）和残差^[2]。这些固有模态函数并非这样的方法产生的，而是来自于信号自身。将EMD信号分解后得到的一系列IMF和残差重新组合相加起来就得到了重构的原始序列^[3]，且失真度极小。把这种方法扩展到二维，即二维EMD方法，将其用于图像压缩。当二维图像被分解为IMF和残差后，对他们进行不同的处理和编码方式。这样的尝试扩大了EMD方法的使用，也使图像信息处理的发展更进一步。

1.2 国内外研究现状

在1998年时，Huang提出希尔伯特-黄变换理论，即HHT。这项理论由两部分构成：经验模态分解和Hilbert谱分析。这是新的有自适应性的分解信号的方法，与傅立叶变换的意义上的频率没有关系，EMD分解的独特之处在于它是以信号中的极值点作为分解尺度的，并且已经应用在故障诊断、信号分析等技术中。近年来，国内外许多学者尝试将其运用到二维信号中，并且已经取得了一定的成果。2011年，宋平舰、张杰等，将EMD二维化，取得了初步发展^[4]。2003年，J.C.Nunes等人把径向奇函数加入到BEMD方法的分量筛选中，开始尝试二维图像的分量提取，BEMD方法有了进一步的完善。该方法的自适应图像分解分量和小波变换、傅立叶变换相比有着后验性的特点。2005年，崔峰等人用BEMD方法得到了不同尺度信息下的信号分量，实现了图像纹理的抽取^[5][6][7]。

经过多年发展，BEMD应用的领域不断扩展，最为广泛的是图像处理领域中。越来越多的学者将BEMD算法用于图像压缩、图像去噪^[8]等技术中，还有医学图像增强^[9]等实际问题上。BEMD通过图像处理，在图像应用领域中得到了大幅度的推广和成功的应用^[10]。

由此我们知道：BEMD是一种新兴信号处理的方法，且在近年来得到了快速发展，它在非平稳、非线性信号方面有着高效的利用，也展现出了强大的优势，但是目前理论还存在诸多问题，部分算法也还不完善，在分解精度和耗时上面还不够理想。所以，在对理论方法存在的不足提出好的理论改进，使整个算法完善提高，应用与更多的领域，是许多学者不断努力和研究的目标。

1948年提出了电视信号的数字化，这是图像编码压缩技术的最早雏形，到现在已经有70年的历史了。由于电路技术发展的受限，上个世纪50-60年代的图像压缩技术在内插复原、亚采样以及预测编码等研究上停滞不前。70-80年代时，矢量量化编码技术和变换编码技术已经获得了相当大的进展。近些年，分形理论，视觉仿真理论、小波变换理论、人工神经网络等发展迅速，越来越多的编码压缩方法涌现，编码技术已经迈向了一个新的发展时期。本文将二维经验模态分解方法应用于图像压缩的研究中，不但给图像编码压缩技术增添了新活力，也推动了经验模态分解方法在多个应用领域的发展，具有一定的创新意义和研究价值。

1.3 本文主要研究内容

本文给出了图像压缩编码的相关知识，介绍了图像压缩技术的性能评估指标。在传统图像压缩方法的基础上，加入二维经验模态分解的方法。这种信号处理的算法在近年来以傅立叶变换为基础的稳态谱和线性分析的基础上有了新的进展。对线性、平稳信号和非线性、非平稳信号都能很好地进行分析。

EMD方法分解出来的信号，是根据其自身尺度的特征分解出来的，这样的分解方法包含了小波变换的多分辨优势，也解决了变换函数的不同选取带来的问题。但其也有自身不足，存在三大问题需要解决：（1）极值点的选取。包络面是由极值点构成的，只有选取恰当的极值点，构造出来的包络面的效果和质量才有保证。在二维信号处理的时候，选择8领域的值作为极值点的参考对象。（2）包络面的构造。需要选择适当的插值函数，构造出来的包络面才有一定的质量。（3）边界效应的抑制。二维信号的分解中对边界效应问题的处理与一维信号不同。边界效应处理不当就会导致在构造上下包络面的时候，数据序列末端的发散，进而影响整个数据序列，造成分解结果失真。

本文采用基于像素的比较极值点来选取图像极值点。使用三次样条插值函数来对极值点进行插值算法，构造包络面。用镜像延拓法来抑制边界效应产生的问题。将二维经验模态分解方法应用于图像压缩。图像经过BEMD处理，分解成一些列固有模态函数和残差，接下来对其进行，极值点压缩、DCT压缩和哈夫曼压缩三种方法对比，并通过改变固有模态函数的数量和压缩算法内的相关系数，得到一系列研究数据。图像重构后得到了较好的结果。

2.图像压缩编码

2.1 图像压缩的信息度量和数据冗余

图像信息的编码必须保证信息源的内容损失不大，甚至不发生变化，这与信息的度量问题有关。从概率统计学的角度来看，信息出现的概率是可以度量的，这个度量方法就是信息量。一般而言小概率的事件所包含的信息量更大，所以事件所包含的信息量与其发生的概率成反比例关系。将信息量定义为信息源发出的所有消息中该信息出现概率的倒数的对数。假设信息源可以发出的消息符号的集合为：，且假设发出符号的概率为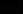 ，那么定义符号出现的自信息量为：

剩余内容已隐藏，请支付后下载全文，论文总字数：18503字