论文总字数：29254字

摘 要

信道编码经过多年的发展，涌现出低密度奇偶校验码、turbo码等一类近香农限编码，为现代通信做出了巨大贡献。而极化码作为一种信道纠错码，所具备的编解码复杂度较低、在理论上被证明能够达到二进制输入离散无记忆信道信道对称容量这两个特点是近些年来极化码得到广泛关注的重要原因。

本文以极化码编解码算法为中心，从以下三方面展开工作：(1) 研究极化码的基础理论知识，进行极化码基础的编解码程序编写和仿真实验。(2)重点研究极化码解码算法，完成能够改善极化码性能的解码算法设计。(3)考虑极化码在硬件平台上的实现。

首先，在极化码的基础理论方面，编码上本文从信道极化的本质出发介绍了极化码的构造方法，详细讨论了生成矩阵的产生和信息位的选取，完成了不同码长和不同码率的实现，并从极化码的非系统编码引申到系统编码，通过MATLAB仿真得到了系统形式的极化码相比非系统形式时性能更优的结论；解码上则将重点放在SC解码和BP解码的算法讨论上，分析了两者算法上的长短，通过MATLAB仿真展示了BP解码相对SC解码在性能上的改善；也简单介绍了极化码的SCL解码和SCS解码，对它们进行了优缺点分析。

接下来，也就是本文的主要工作成果，对极化码进行改进的解码算法设计。本文在BP解码的基础上进行解码算法的研究，提出了在BP后面串联OSD的极化码解码算法：极化码迭代排序统计译码方法，并在极化码FER性能和BER性能上都取得了一定程度的改善。内容上简单介绍了迭代排序统计译码方法的背景；将解码流程分为系统形式极化码的BP解码、零阶OSD译码处理和一阶OSD译码处理三个阶段，详细论述了迭代排序统计译码方法应用于系统形式极化码的具体算法实现；结合MATLAB仿真分析了迭代排序统计译码方法的性能，体现了该算法的优异性；也讨论了当前算法的不足之处和改进空间。

最后，本文也简单考虑了极化码的硬件实现，简单讨论了解码器硬件实现所需注意的算法方面的改变；从解码器硬件架构和重要组成部分、解码器时序的实现两个方面出发介绍了SC解码器和BP解码器的硬件实现，并分析了当前解码器设计的效率和特点。

关键词：信道极化，极化码，置信传播，排序统计译码

Abstract

Codes near channel limit such as low density parity-check codes and turbo codes have made great contributions to modern communication system since years of development. As a kind of channel error correcting codes, polar codes have attracted widespread attention because of its capacity-achievability and low complexity.

The paper focuses on the coding and decoding of polar codes and expands as follows: (1)studying the basic theory of polar codes, programming and simulating; (2)studying the decoding of polar codes and trying to design a better algorithm of decoding; (3)considering the implement of polar codes on the hardware platform.

Firstly, in the terms of coding of polar codes, the paper introduced the construction of polar codes from its nature of channel polarization. The paper talked about how to construct the generate matrix and how to choose the place of information bits, according to which polar codes with the different rate and different length could realize. Then the paper expanded traditional nonsystematic coding of polar codes to systematic coding, and drew the conclusion that systematic polar codes have better BER performance than the nonsystematic polar codes. In the terms of decoding, the paper focused on the basic successive cancellation decoding and belief propagation decoding and analyzed their strength and weakness through a simulation. And the successive cancellation list decoding and successive cancellation stack decoding were also introduces simply.

Secondly, the paper proposed a new decoding algorithm for polar codes, which is the major achievement of this paper. The scheme was to introduce ordered statistic decoding and to make it in series with belief propagation decoding, for which we can call it BP-OSD. The paper talked about the background and significance of this scheme. Then, the specific algorithm was discussed in three parts: BP decoding of systematic polar codes, order-0 OSD, and order-1 OSD. The performance of this decoding algorithm was also analyzed with the results of MATLAB simulation. And the deficiencies and space to improve were discussed, too.

Lastly, the paper also took the hardware implement of polar codes into consideration. The change from theory to actual implement was simply discussed. Then, the SC decoder and BP decoder was introduced from the aspect of hardware architecture and component and that of the implement of the sequence respectively. The paper also analyzed the efficiency and the features of the design at last.

KEY WORDS：channel polarization, polar codes, belief propagation, ordered statistic decoding

目录

摘要 I

Abstract II

第一章 绪论 1

1.1. 引言 1

1.2. 极化码的发展与研究现状 1

1.3. 极化码的应用 2

1.4. 论文的主要研究内容和结构安排 2

第二章 极化码的编解码 3

2.1. 极化码的编码 3

2.1.1. 生成矩阵的产生 3

2.1.2. 信息位的选取 6

2.1.3. 极化码的系统编码 7

2.2. 极化码的解码 9

2.2.1. SC解码 9

2.2.2. BP解码 12

2.2.3. SCL解码 14

2.2.4. SCS解码 15

2.3. 本章小结 15

第三章 极化码迭代排序统计译码方法 16

3.1. 迭代排序统计译码方法的背景 16

3.2. 迭代排序统计译码方法的具体算法实现 16

3.2.1. 系统形式极化码的BP解码 16

3.2.2. 零阶OSD译码处理 17

3.2.3. 一阶OSD译码处理 17

3.3. 迭代排序统计译码方法的性能分析 18

3.3.1. 与基础的BP解码比较 18

3.3.2. 与极化码其他解码算法比较 18

3.3.3. 与其他编码方式(turbo)比较 18

3.4. 迭代排序统计译码方法的优点与不足 20

3.5. 本章小结 21

第四章 极化码的硬件实现 22

4.1. 对数似然比的考虑 22

4.2. SC解码器 22

4.2.1. 硬件架构和重要组成部分 22

4.2.2. 时序的实现 23

4.2.3. 解码器效率 24

4.3. BP解码器 24

4.3.1. 硬件架构和重要组成部分 24

4.3.2. 时序的实现 25

4.3.3. 解码器效率 26

4.3.4. 解码器的设计特点 26

4.4. 本章小结 26

第五章 总结与展望 27

5.1. 文章总结 27

5.2. 下一步工作计划 27

致谢 28

参考文献(References) 29

绪论

引言

自从1948年C. E. Shannon在他的论文[1]中提出有噪信道编码定理，指出信息传输速率小于信道容量时存在可以使得传输错误概率任意小的编码后，人们就致力于寻找这种能够达到信道容量的编码方式，然而这几乎一直是个不可实现的目标。在这个漫长的过程中，低密度奇偶校验(low density parity check, LDPC)码和turbo码等一类近香农限编码被相继提出，然而它们都不能在理论上被证明能够达到香农极限。直到2009年，E. Arikan在他的论文[2]中首次提出了信道极化的思想，并将以此为基础构建的码命名为polar codes——极化码。他在理论上证明了极化码能够在任意给定的二进制输入离散无记忆信道(binary-input discrete memoryless channel, BDMC)中达到对称信道容量，而与此同时又只有的编解码复杂度。

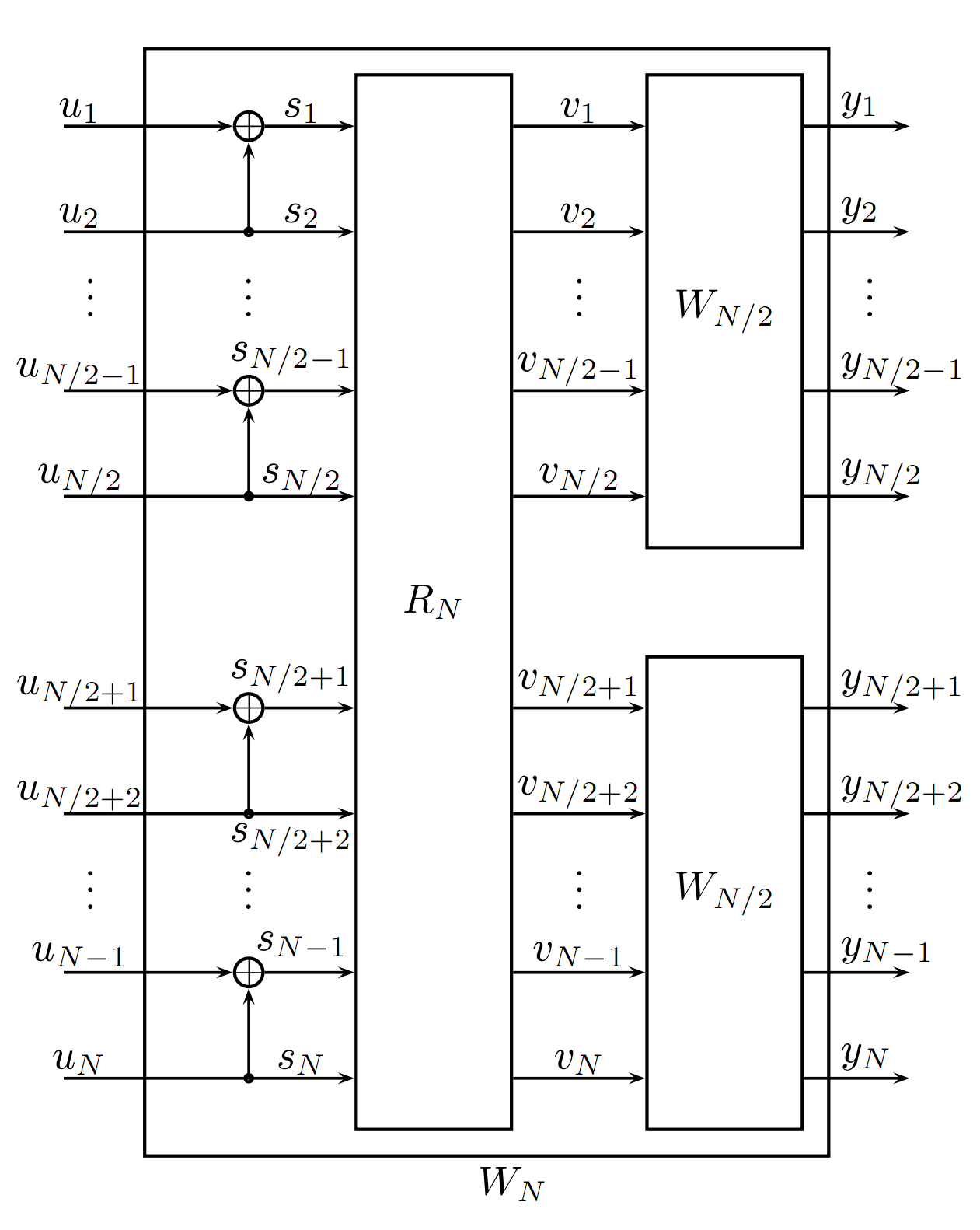
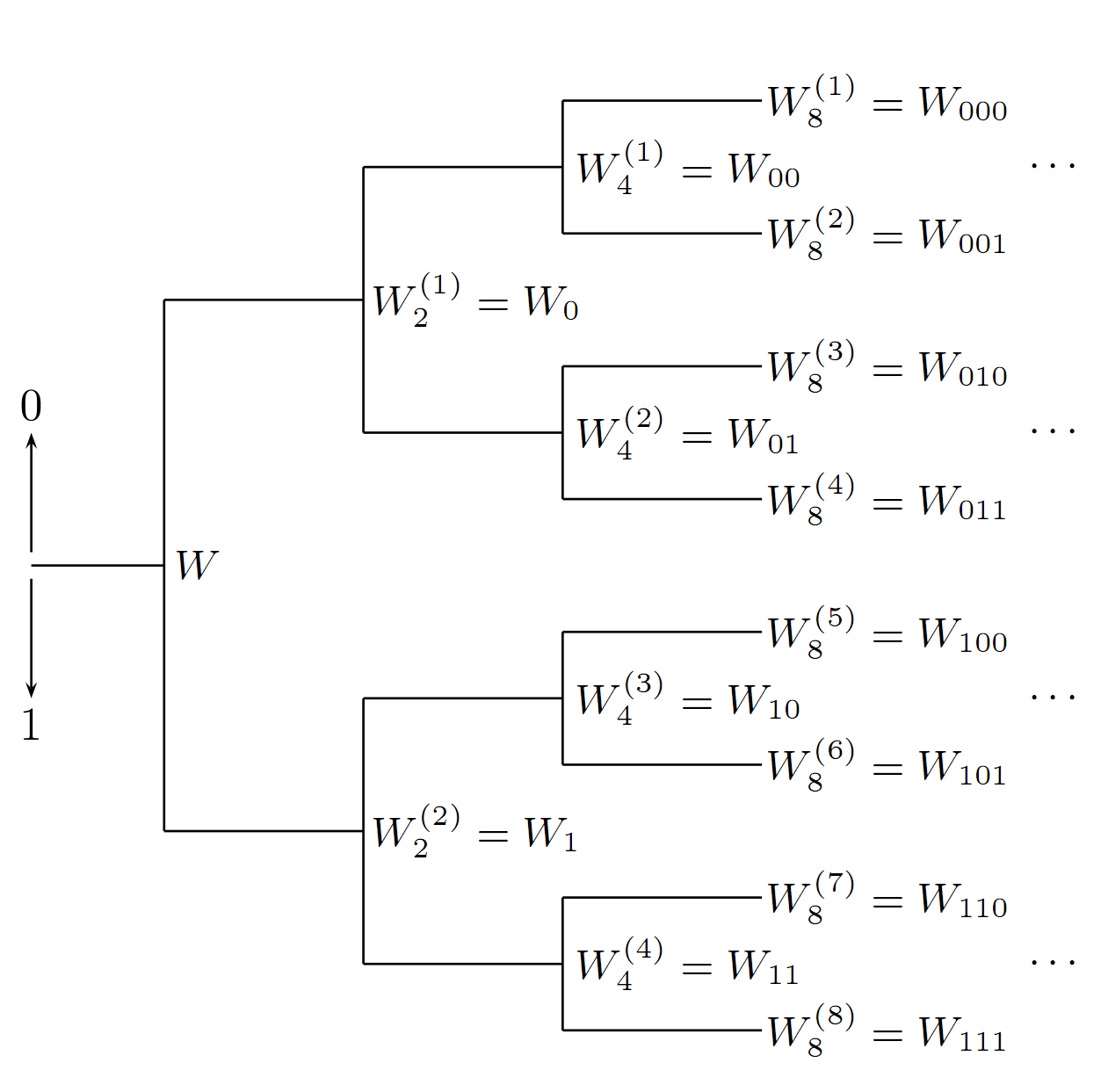
信道极化，是通过将N个BDMC信道合并、再将合并后的信道拆分成相关信道这两个阶段[3]实现的。当N很大时，信道在经过这两个阶段后被极化，一部分信道的容量趋于1，另一部分信道的容量则趋于0。也就是说，理想状态下，信息在传输时要么通过几乎无噪声的信道，要么通过几乎完全是噪声的信道。极化码就是一种让信息比特通过那些无噪声的信道传输，而冗余位则通过那些完全是噪声的信道传输的编码方式，其中冗余位是发送方和接收方都知道的一些固定比特。

极化码的发展与研究现状

极化码的提出引起了信道编码领域的广泛关注。在Arikan提出二进制输入的极化码后，由此扩展而来的多进制输入的极化码也在论文中[4]被提出。编码方面，构造极化码的核心矩阵也在论文[5]中被扩展为的核心矩阵。

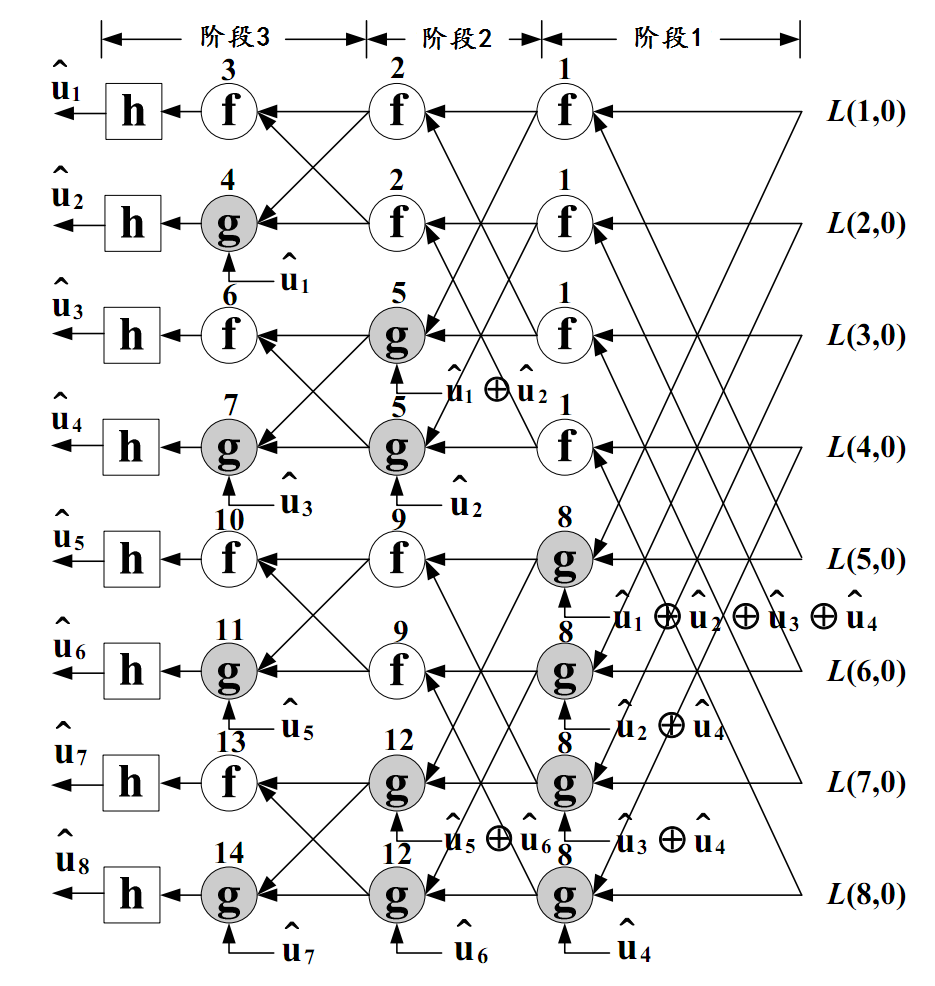
论文[6]讨论了码长和码率对于信道极化的影响，并发现在实际应用中，有限的码长无法保证极化码的良好性能。事实上，Arikan提出的连续删除译码(successive cancellation, SC)算法作用在有限长度的极化码上表现出来的性能并不那么让人满意。为此，很多其他的解码技术被应用到极化码上来提高极化码的性能。置信传播译码(belief propagation, BP)算法首先被发现在误比特率(bit error rate, BER)性能上相对SC解码有明显的改善[7]。随后，基于SC算法的涉及到多个路径而非单一路径的列表解码(successive cancellation list, SCL)算法[8]和堆栈解码(successive cancellation stack, SCS)算法[9]也被相继提出，来近似达到最大似然解。此外，A. Eslami和H. Pishro-Nik还提出了将极化码与LDPC码级联来进一步提高其性能的方案[10]。这些技术都保留了原有的编码方案，而将重点集中在解码算法的改进上，这些改进是以额外的解码复杂度为代价的。

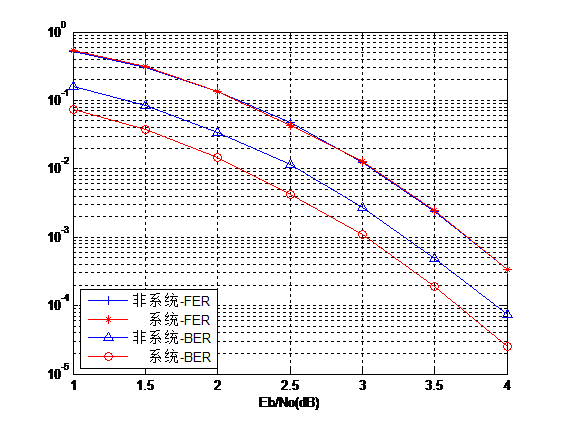
改善极化码性能的另一个方向是从编码入手。传统的极化码编码是非系统形式的，而Arikan在论文[11]中介绍了系统形式的极化码编码方案，并在BER性能上获得了很大的改善。系统形式极化码的基本思想是利用码字x的一部分来传输信息比特，而不是直接使用源信息u。它的优点在于，获得性能改善的同时仍然保留了较低的解码复杂度，而编码方面也只需要增加少量的步骤。

极化码的应用

Arikan把极化码作为一种信道编码提出来，而论文[12]中则将极化码扩展到了二进制信源编码，发现极化码在Slepian-Wolf编码上可以获得很好的应用。论文[13]中研究了极化码在有损信源压缩方面的应用，发现极化码能够在对称二进制信源压缩上达到率失真界，并且在解决如二进制Gelfand-Pinsker问题、二进制Wyner-Ziv问题等很多多端口网络问题时都是最佳的。论文[14]中也提出，信源压缩不同于信道纠错环境，能够保证极化码的按序译码不造成错误传播，并得出了极化码在信源压缩方面是渐进最佳的结论。极化码能够对独立同分布的信源以最低的编解码计算复杂度和最小的速率完成无损压缩，论文[15]以此为基础进行了向q进制信源的扩展，提出了一种新的极化码信源压缩方案。

Arikan提出的极化码针对的是单用户信道，信道极化后的结果要么是完全无噪声的信道，要么是完全是噪声的信道，而论文[16]中则把极化码推广到了两个用户的多用户信道，扩展后信道极化的结果有五种可能，有趣的是扩展后这种针对多用户信道的极化码相对原本针对单用户信道的极化码来说并没有增加编解码的计算复杂度。论文[17]中把极化码推广到了m个用户的二进制输入多址接入信道(binary-input multiple access channel, BMAC)，并研究了极化码在MAC信道下的构造问题。论文[18]中则提出可以将加性高斯白噪声信道(Additive White Gaussian Noise, AWGN)映射为m个用户的BMAC信道，这样就提供了一种极化码在连续信道中的编码方案。

论文的主要研究内容和结构安排

文章主要针对极化码的编解码理论进行了深入的研究，并对极化码基础的SC解码和BP解码做了MATLAB仿真实验；此外，本文也研究了系统形式的极化码，并以此为基础提出了极化码的迭代排序统计译码方法，在极化码的误帧率(frame error rate, FER)和BER性能上都获得了一定的改善；最后，文章探讨了极化码硬件实现的可行性和效率，对极化码未来能否广泛应用到通信系统中做出了展望。

剩余内容已隐藏，请支付后下载全文，论文总字数：29254字

相关图片展示：