论文总字数:22144字
摘 要
本文主要讨论LC-VCO的起振时间问题,在VCO各参数中,起振时间是至关重要的一个,在振荡周期内,输入幅度和振荡起振的时间的关系尤为重要,接收机的灵敏度如何,直接取决于起振时间变化对输入信号幅度是否足够敏感。
首先,通过对晶体压控振荡器的起振时间做深入的研究探讨,说明其起振原理,并与LC压控振荡器进行比较。建立LC-VCO模型,利用simulink对其传输函数进行行为级仿真,探讨振荡器各个因素对起振时间的影响,并确定在何种情况下振荡器起振时间对输入信号幅度最为敏感。
关键词:LC压控振荡器,起振时间,输入信号幅度
A Study on Start-up of LC-Voltage-Control Oscillator
Abstract
This paper describes the evolution of the start-up of LC-voltage-control oscillator and focuses on the start-up time which among all the parameters is a very important one. The sensitivity of the receiver mainly depends on whether the start-up time of oscillator is sensitive to the change of
input amplitude.
First of all, the start-up process of the crystal-voltage-control oscillator is examined then compared to the LC-voltage-control oscillator to introduce the way it works. Then the model of LC-voltage-control oscillator is built on SIMULINK platform for the system to be tested figuring out the influence of every elements on start-up time and under which condition is the start-up time most sensitive to the input amplitude.
KEY WORDS: LC-voltage-control oscillator, start-up time, input amplitude
目 录
摘要 ……………………………………………………………………………………Ⅰ
Abstract …………………………………………………………………………… Ⅱ
第一章 绪论………………………………………………………………………………1
1.1 引言…………………………………………………………………………1
1.2 振荡器基本原理……………………………………………………………2
第二章 晶体振荡器起振时间……………………………………………………………2
2.1 本章摘要……………………………………………………………………2
2.2 谐振电路的小信号分析……………………………………………………4
2.2.1 简化等效电路的小信号分析………………………………………8
2.2.2 完整等效电路的小信号分析………………………………………10
2.3 计算谐振器的电流初值……………………………………………………10
2.4 反相器工作的初始阶段……………………………………………………11
2.5 本章小结……………………………………………………………………18
- LC振荡器起振时间………………………………………………………………19
3.1 LC振荡器原理………………………………………………………………19
3.2 SIMULINK仿真平台简介……………………………………………………20
3.3 LC振荡器起振的仿真………………………………………………………21
- 超再生振荡器的起振……………………………………………………………23
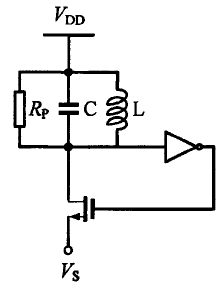
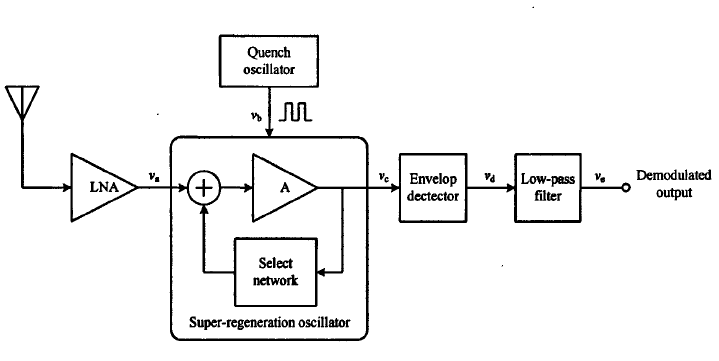
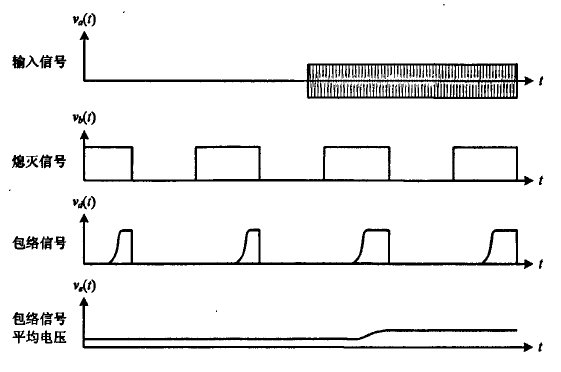
4.1 超再生接收机原理…………………………………………………………23
4.2 超再生振荡器的起振时间…………………………………………………24
4.3 基于MATLAB的仿真…………………………………………………………26
第五章 总结与展望………………………………………………………………………32
致谢 ………………………………………………………………………………………32
参考文献(References) ………………………………………………………………33
- 绪论
1.1引言
VCO即压控振荡器,是射频电路不可缺少的重要构成。射频电路主要采用调制解调方式,故严重依赖本振。而在现代通信技术中,要求采用复用、跳频等新技术,利用电压来控制振荡回路中电容的电容量,从而改变振荡回路的谐振频率是能够帮助实现这些技术的有效手段。与普通本振相比,压控振荡器在谐振回路中多出了电控器件,例如变容二极管;一般的压控振荡器主要以克拉泼振荡器形式存在,以保证电路工作点的稳定和Q值的稳定。
压控振荡器在通信领域有着极广泛的应用,是射频电路的重要组成部分。 根据其产生的波形可分为谐波振荡器和张弛振荡器,根据其组成结构可分为LC压控振荡器、RC压控振荡器和晶体压控振荡器。其主要技术参数有:频率受控范围、线性度、压控灵敏度、调制带宽、噪音、工作电压等。
在通信电子行业迅速发展的今天,市场对电子设备的要求越来越高,尤其是振荡器这种基础部件的要求更是如此。但很多年来,我国在此方面的研究投入重视程度堪忧,无论是军用还是民用,仅仅局限于引进和改进,无法达到质的跨越,缺乏自主知识产权(IP),这也是我国电子通信行业发展滞后于大多数发达国家的原因之一。在我国,多数厂家依然在使用传统的双极工艺,产品的成本、体积和重量都很大,性能不足且稳定性差,同时难以和主流CMOS工艺集成。这些都成为了我过相关领域发展的瓶颈。但从另一个角度看,这种落后也说明了国内此领域的市场有着很大的发展空间,自主研究高性能高质量且低成本的压控振荡器有着非凡的意义和广阔的市场前景。
关注振荡器本身,起振时间是其很关键的一个参数,因为在振荡器达到正常工作振幅前,不可避免地会经过一个起振过程,此过程所需要的时间会影响到振荡器的设计方案、实际性能和工作稳定程度。更直接地,起振时间对于输入信号幅度变化的敏感程度直接决定了接收机的灵敏度。所以在一个振荡器的研究和设计过程中,我们总是希望其起振时间尽可能短,即尽快达到稳定震荡幅度,并且起振时间能够对输入信号的幅度变化保持高度敏感,以提高接收机的灵敏度。
1.2振荡器基本原理
振荡电路是收发设备的基本电路,它最直接的作用是产生一定频率的交流信号,是一种转换能量的装置,能够将直流电能转换成交流电能,在许多电子设备中均有广泛应用。例如:晶体振荡器可用于制造石英表,晶体振荡器即石英晶体谐振器和石英晶体时钟的统称,但因为在实际生产应用中,谐振器的使用占绝大部分,所以一般提到的的晶体振荡器指的就是谐振器;调幅收音机可由用户自主调节频段,并把天线所接收到的信号处理成声音播放;电台使用带有振荡器的发射器制作载波,调幅收音机中使用特殊形式的振荡器:谐振电路进行调谐,甚至在金属探测器、眩晕枪中都有振荡器的应用。
最常见的振荡器就是时钟的钟摆,给予它一次推动,它就会开始做有规律的摆动,这一规律就是它会在单位时间内振荡一定的次数,而控制其频率的是摆的长度。要使得物体振荡,能量必须在两种形态之间来回转换,并且转换过程中的能量损失要足够的小。以刚提到的钟摆为例,给予的推动是这个系统的初始能量。当摆达到最高点时,它其实是静止的,所有的动能都转化成为重力势能;这一时刻之后,摆会在重力作用下向反方向摆动,重力势能逐渐转化为动能,也就是速度越来越快,直至摆运动到最低点时,最多的势能转化成了动能;在此之后,摆最终会到达另一侧的最高点,继而再次下落,如此往复,能量在两种形式之间来回转化,形成了所谓的“振荡”。但是这样的振荡不会无限往复下去,因为在摆的运动过程中总是会损失一定的能量,在足够长的时间后,初始能量被损耗完毕,振荡就会停止。所以钟摆里必然会有弹簧在摆的每一个振荡周期里给予其一定的能量作为补充,而使用者为摆钟上发条就是一个将若干能量储存在弹簧里的过程。
电子振荡器的核心原理和摆钟无异,也需要能量在两种形式之间来回转换。所谓电容器,就是储存电荷的容器。其中存有的正负电荷等量地分布在两块不直接导通的导体上,其基本模型为两块带等量异种电荷的导体板中间相隔以介质,实际上是一种储存电场能量的器件。而电感是能够将电能转化为磁场能量储存起来的器件,所以理论上我们需要一个电容和一个电感就可以构成前述的能量在不同形式间的转换而形成振荡。这就是振荡器最基本的工作原理。
第二章 晶体振荡器起振时间的研究
2.1本章摘要
这一章节描述了基于振荡器的CMOS反相器中信号在起振阶段的变化情况。表征震荡幅度指数增长的时间常数由谐振电路的小信号分析决定,这一时间常数与电路参数间的关系已经测得。为反相器供电时,电流和电压的初值估计已经明确。振荡器在各种条件、不同类型谐振器状态下的起振情况也已进行分析。通过已知条件,可以计算出整个振荡器系统的起振时间。
PIERCE振荡器是在涉及CMOS技术的电路中最常用的振荡器类型之一。因此,我们有必要去了解其各种特点,这其中就包括它的起振机制。鉴于已有诸多学者对其起振的条件做了研究分析,本文会将重点放在起振阶段的振幅变化上。[1][2]
本部分将着眼于振荡电路的小信号分析。我们会计算谐振器中的电流的幅度变化并分析起振时的条件。下一步,通过分析反相器开始工作时的电压,确定电流初值。在计算总起振时间时,会考虑不同类型的谐振器。
2.2谐振电路的小信号分析
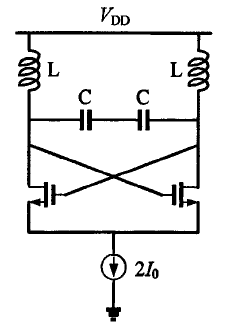
从起振阶段开始,振荡器的信号振幅就很小,属于小信号。故对于图1中的PIERCE CMOS振荡器,可用图2中(a)(b)来表示其小信号等效电路。图2(a)中所示简化等效电路中信号的变化可通过描述电压电流关系的等式确定。图2(b)展示了振荡器更加完整的等效电路,其中包括一些电阻部分。为了确定此电路的起振情况,需要在频率仅由谐振器确定的前提下进行进一步分析。
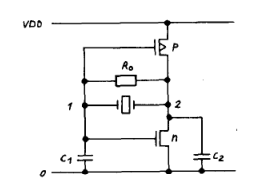
图2-1 Pierce型振荡器电路
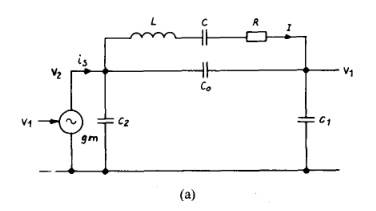
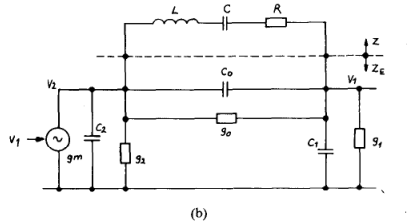
图2-2 (a)简化电路的小信号等效模型
- 完整电路的小信号等效模型
2.21 简化等效电路的小信号分析(图2(a))
在图2-1(a)所示等效电路中,L和C是谐振器中的变量,R代表其损耗。C1和C2是构成振荡器必要的电容。C0代表与谐振器并联的电容,其中包括它本身的静态电容。跨导gm是激励晶体管p和n的跨导总和。
假设t=0时,谐振器两端电压v(0)=0,此时流经电感L的电流与其对时间的倒数分别为i(0)和i’(0)。由拉普拉斯变换得到的描述此电路电流和电压的等式分别如下:
(1)
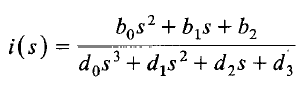
其中
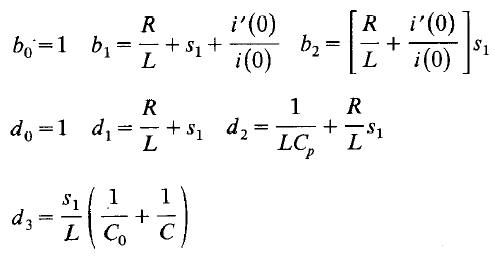
其中Ct代表谐振器总并行电容,电容Cp与电感L可以粗略的确定谐振电路的频率
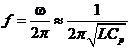
电流值作为函数i(t)的因变量,可由(1)式的逆变换得出。为确定i(t),有必要求分母特征方程的根。由于此电路为谐振电路方程会有一个实根和两个共轭复根。
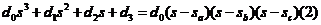
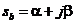
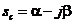
Sa ,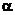 和
和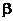 的值可由Cardan 算法[3]确定。
的值可由Cardan 算法[3]确定。
这样,我们容易得到,电流i作为时间t的函数如下
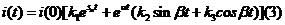
其中k1,k2,和k3的值取决于i(0)和i’(0)。i(t)在初期随时间衰减,各个变量幅度的指数变化仅由系数α决定。图3中曲线a表示α作为gm的函数的值,gm对应一带有4-MHz石英谐振器的电路:C=8fF,L=0.2H,R=75Ω,C0=3pF,C1=C2=10pF。若gm<gmmin,振幅减小,振幅会随gm的增加而增大,当gm=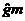 时,其值最大。若gm>
时,其值最大。若gm>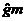 ,谐振电路相移将变得明显,起振会被放慢。若gm>gmmax,甚至不会发生振荡。
,谐振电路相移将变得明显,起振会被放慢。若gm>gmmax,甚至不会发生振荡。
将α=0代入与三阶方程(2)相关的等式,可以确定gm的最小值和最大值。
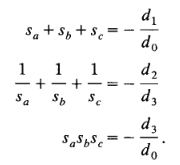
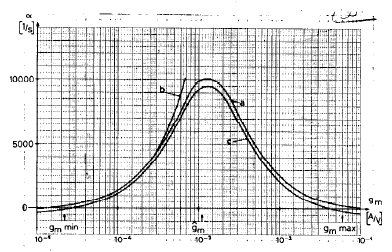
图2-3 计算中涉及的曲线
剩余内容已隐藏,请支付后下载全文,论文总字数:22144字
相关图片展示:
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


