降水椭球粒子群取向正态分布的模拟

论文总字数：16743字

目 录

1 引言 …………………………………………………………………(1)

• 1. 研究意义……………………………………………………………………(1)
  2. 国内外研究情况……………………………………………………………(1)

2 模拟过程……………………………………………………(1)

2.1 模拟依据……………………………………………………………………(1)

2.1.1 Gamma雨滴谱参数范围………………………………………………(3)

2.2 程序设计……………………………………………………………………(3)

2.2.1 倾斜椭球形粒子群分布程序设计……………………………………(3)

2.2.2 Gamma雨滴谱分布函数………………………………………………(6)

2.3 程序运行结果………………………………………………………………(6)

3 模拟结果分析…………………………………………………(7)

3.1 图形分析………………………………………………………………………(8)

3.2 数值分析………………………………………………………………………(8)

4 实例模拟………………………………………………………(8)

4.1 积雨云实例模拟………………………………………………………………(8)

4.2 层状云实例模拟………………………………………………………………(9)

4.3 积层混合云模拟………………………………………………………………(10)

4.4 对2009-2010年南京江淮梅雨锋暴雨的模拟………………………………(11)

4.4.1 对淮南（2009.07.07）江淮梅雨暴雨情况的模拟……………………(12)

4.4.2对南京浦口（2009.07.07）江淮梅雨暴雨情况的模拟………………(13)

4.4.3对南京浦口（2010.07.12）江淮梅雨暴雨情况的模拟………………(14)

4.4.4对南京江宁（2010.07.12）江淮梅雨暴雨情况的模拟………………(15)

5 结论……………………………………………………………(16)

6 讨论……………………………………………………………(16)

参考文献…………………………………………………………(17)

致谢………………………………………………………………(17)

降水椭球粒子群取向正态分布的模拟

翟昭雯

, China

Abstract:The rainfall radar can obtain the information such as the intensity and position of the precipitation by the backscatter of the precipitation particles. The intensity of the radar echo is related to the factors such as the drop spectrum, shape, particle position distribution and dielectric constant of the cloud particles in the backscattering volume. From the radar echo signal we can understand the nature of scattering particles and precipitation in the water content or rainfall. And we usually need to use small canting ellipsoid particles to approximate simulation. This project focuses on the distribution of simulated precipitation particle swarm population. We will simulate according to the different kinds of precipitation where the position as well as the orientation angle of the canting ellipsoid particles are Gaussian distribution, and the size of the ellipsoid particles are Gamma raindrop spectrum distribution. It is expected to work out the possible influence of small canting ellipsoid particles on radar detection in each case. So as to provide the basis for atmospheric microwave remote sensing, especially for improving the accuracy of weather radar to measure the accuracy of precipitation.

Keywords: Ellipsoid particles；canting; normal distribution; Gamma raindrop spectrum

1 引言

1.1 研究意义

降水是指空气中的水汽冷凝并下落到地表的现象。如今对于降水要素的探测也是一个难点。当发生降水时，降水粒子以一定数浓度在空间内下落，如果不考虑外力因素，降水粒子应为球形，但由于实际大气中水平方向、垂直方向上风切变等不确定因素的存在，会影响降水，使得降水粒子发生不同程度的倾斜和形变，产生形变后会影响到粒子的散射、衰减等特性，继而对测雨雷达的探测结果产生影响。并且，对于不同类型的降水，具体情况也不同，本文将按照各情况，对椭球形降水粒子的分布进行模拟和讨论。

雨滴谱是雨滴数浓度随雨滴粒子尺度大小变化的函数，雨滴谱的谱形与诸多因素相关，如时间，空间，尤其是与它的观测对于云以及降水物理的观测十分重要，在气象相关的科学领域范围内也有十分重要的意义和应用价值。通过不同类型降水的雨滴谱分布，我们可以了解到一些重要的降水要素值，例如，降水粒子的数浓度，含水量，谱形分布等等，除此之外，对于降水结构的研究和降水演变过程的探测以及预测也有不可或缺的作用。本文采用Gamma的雨滴谱分布对各种类型的降水实例进行模拟，由于降水类型不同，每个模拟中的具体参数也有差异。

1.2 国内外研究情况

Barber(1975)认为, 降水粒子散射理论的发展和不同形状、不同相态粒子散射特性的计算研究能够为雷达观测结果提供了相比较Mie 理论和Rayleigh 理论而言更符合实际的解释和分析依据。Atlas(1953) 用Gans 散射理论研究了小旋转椭球粒子的散射特性。张培昌等根据小旋转椭球散射的Gans 理论中, 推导出了小旋转椭球粒子群旋转轴在均匀随机取向情况下的平均衰减截面。胡方超等（2004）考虑到了小旋转椭球粒子群旋转轴的空间取向的正态分布随机性, 研究了小旋转椭球粒子群旋转轴取向在正态分布情况下的平均衰减截面。胡方超，张培昌等（2013）根据双线偏振雷达探测小椭球粒子群的雷达气象方程，对Gamma雨滴谱采用数值模拟的方法研究了雷达天线仰角和粒子谱参数改变时和对粒子群旋转轴在空间作垂直一致取向时给差分反射率因子带来的影响。本文将利用Matlab程序对降水椭球粒子群分布的形态特征进行模拟。

2 模拟过程

2.1 模拟依据

单位体积内，降水粒子群由一定数浓度的单个降水粒子组成，而对于单个降水粒子，约束条件有位置，大小以及形态等要素，对于各个粒子的位置要素，我们采用正态分布的方式来模拟，用Matlab的语言编写，形如：

Rx=normrnd(5,3,1,100);

Ry=normrnd(5,4,1,100);

Rz=normrnd(5,6,1,100);

（Rx,Ry,Rz）为粒子坐标，对三个坐标分别取以5为期望值，3、4、6为方差值的100个正态分布随机数，于是对于Rx，Ry，Rz，可以分别得到三个1100的矩阵，对于第i个降水粒子，其球心坐标即为（Rx(1,i),Ry(1,i),Rz(1,i)），由此可以首先确定降水粒子群中各粒子的位置。

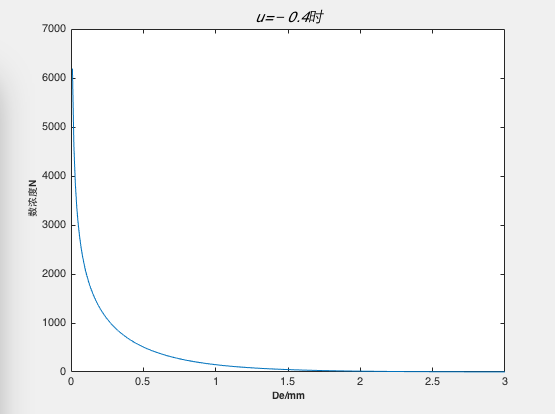
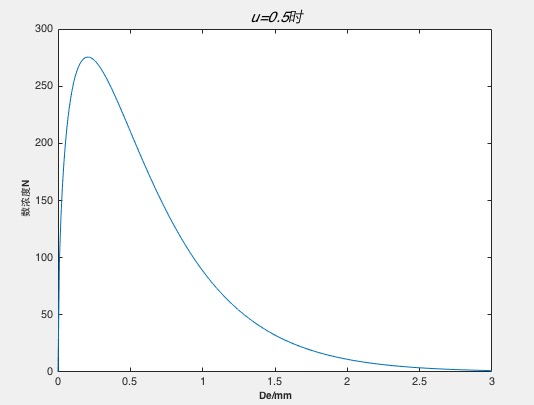
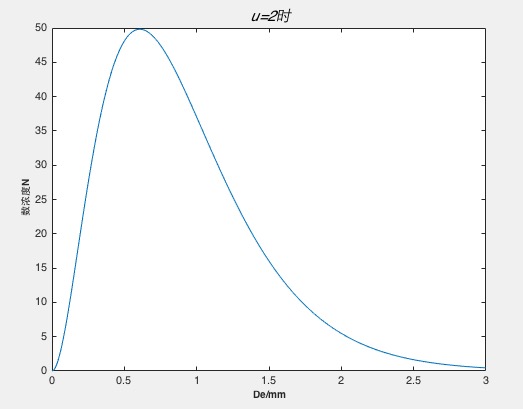
对于降水粒子个数的限制，我们采用Gamma雨滴谱分布函数来拟合降水粒子群的分布。Gamma雨滴谱分布具有普适性，即可以反应层状云雨滴谱分布，又可较理想的描述积雨云和积层混合云的雨滴谱分布。Gamma雨滴谱分布函数：

， (1)

式（1）中，为滴谱的浓度，是单位尺度间隔时，单位体积内降水粒子的个数，单位为：/mm*m^3；为滴谱的中值直径，单位为：mm；为谱的形状参数；为椭球降水粒子等效直径，单位：mm；

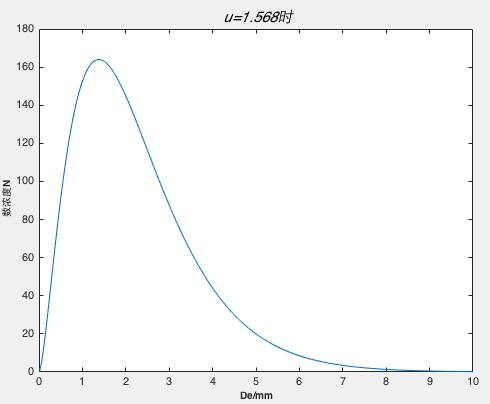
Gamma雨滴谱分布函数的含义为在指定等效半径De的情况下，得到此时对应下的数浓度。故，若我们需要拟合De在0mm至10mm内时降水粒子的分布情况时，则需要先对Gamma雨滴谱分布函数进行积分，然后取整得到当等效直径De由0mm至10mm时，降水粒子在各自区间对应形态下的个数，即：

N=， (2)

对于等效半径De的讨论情况如下：

因我们现在所讨论的降水粒子呈椭球形分布，故存在有短半轴b和长半轴a，单位：mm；当De在0mm至0.28mm时，降水粒子表现为球形，而对于球形降水粒子，短半轴的长度与长半轴的长度相等，即a=b=c；De在0.28mm至1mm范围内时，降水粒子呈现椭球形，对于椭球形降水粒子，长半轴a与短半轴b的关系为：

a/b= ,0.28 (3)

(4)

为雨滴下落末速度，单位：cm/s；ρ为饱和空气水汽密度，近地面时，；为水的表面的张力系数，值为：；对于区间范围内已知的以及指定的短半轴长度b，长半轴a的大小也就可以得到了。并且，由于a与b的关系呈现为分段函数的形式，所以模拟分布时需根据a与b的关系，按照三段区间来模拟。至此，对于椭球形降水粒子群的模拟要素中，已成功得到了椭球降水粒子的位置和大小限制条件。

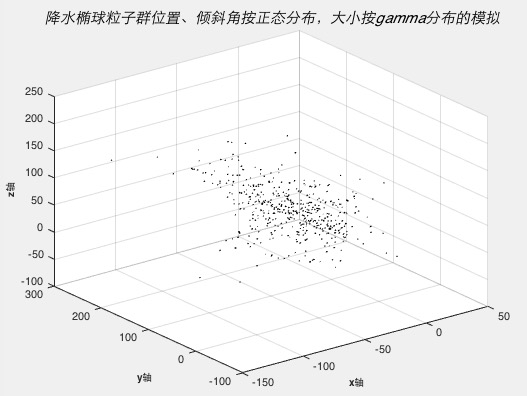
对于球形降水粒子，表现为各向同性，不具有方向性，故不存在旋转；然而在属于0.28mm至10mm区间内时，长半轴a与短半轴b的大小不等，故降水粒子呈现椭球形，对于椭球形降水粒子，由于存在长轴和短轴的区别，会出现旋转轴的倾斜，即旋转轴和长轴之间会产生一定的角度，所以在模拟的时候需要对椭球形降水粒子群中的每个椭球粒子单独建立一个坐标系进行一定角度的旋转然后再将每个单独的已倾斜椭球粒子平移至总坐标系中，倾斜的角度按照正态分布随机数选取。由此可以得到降水椭球粒子群的分布拟合。

剩余内容已隐藏，请支付后下载全文，论文总字数：16743字

相关图片展示：