论文总字数:27002字
目 录
1 引言 1
2 ANUSPLIN介绍 1
2.1 插值算法介绍
2.2 参数率定
2.3 最佳模型选择要求
3 研究区域与方法 4
3.1 研究区介绍
3.2 数据准备
3.3 研究方法
4 结果与讨论 6
4.1 相关性分析
4.2 模型精度评价与最优模型选择
4.3 插值结果分析
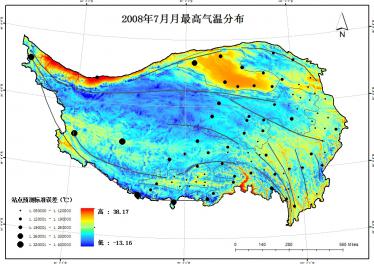
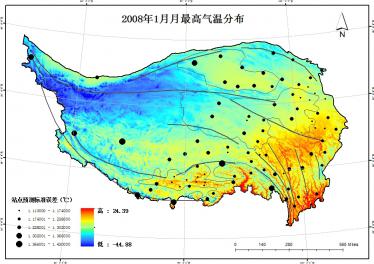
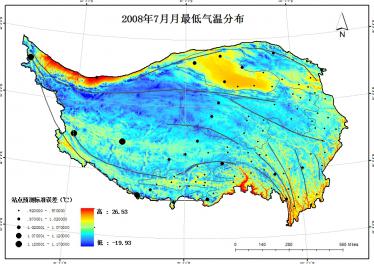
4.3.1 青藏高原气温分布
4.3.2 青藏高原降水分布
5 结论与展望 16
参考文献 17
致谢 20
附录 21
基于ANUSPLIN软件的青藏高原气温和降水的插值与验证
唐梦馨
,China
Abstract:Here we attempt to use ANUSPLIN,a professional climate elements interpolation package,to interpolate average temperature,maximum temperature,lowest temperature and precipitation in monthly scale with 1,4,7,10 month,based on the observation data of 175 available meteorological stations in 2008 over the Qinghai-Tibetan Plateau and its surrounding areas.During the interpolation,we performed to ensure the best interpolation model and estimate the predictive accuracy through using different combinations with the three variables,including longitude,latitude and elevation.The results indicated that,in the Qinghai-Tibetan Plateau,the best temperature interpolation model,which can get high fidelity and smoothness,is a three-variate thin plate smoothing spline function with 3 spline order,developed in which longitude and latitude were used as two independent variables and elevation were a covariate.The three variables can be applied to the spatial interpolation of precipitation in the Tibetan Plateau,but the predictive accuracy can't meet our high requirements,because of the complexity of the precipitation,we need a further study to optimize our precipitation interpolation results.
Key words:ANUSPLIN;Qinghai-Tibetan Plateau;temperature;precipitation;spatial interpolation
1 引言
空间气象数据是气候、水文、农林建设、生态及环境建设等相关研究领域的基础参数。作为一种典型的地理要素,它是多数地学模型和气候模型模拟时必不可少的输入参数,并在很大程度上影响着各种模型模拟获得的结果。气温和降水是各类研究中使用最多的气象要素,通常可通过研究区内的气象观测站点来获得。但由于地理条件的限制与经济成本的制约,气象测站存在空间分布不均匀,密度不足等问题,严重影响了气象数据使用的精确性,对进一步的空间分析与地学建模造成了困难[1]。
目前,通过地理信息系统与统计学等多个学科的综合研究,研究人员基于空间相关性的基础,在已有观测数据的气象站点上,通过一定的数学方法来对邻近测站区域的气象要素进行估计与拟合,从而获取观测站点以外研究区域的气象数据。该方法即为气象要素空间插值法,能够将空间上离散的站点观测数据转换为连续的气象要素曲面,便于对气象要素分布进行建模研究。近年来,众多学者对气象要素插值法进行了详细的探讨与研究,主要集中于插值算法原理理论、各个算法对研究区的适用性以及插值精度提升等几个方面的研究。李新(2000)等学者根据现有插值方法的基本假设与数学本质,将插值方法分类为几何方法、统计方法、地统计法、函数方法、随机模拟方法、物理模型模拟方法和综合方法七类[2-4]。目前,在气象要素空间化的研究中,出于数据特点、算法复杂度和插值精度等几方面的综合考虑,常用的插值方法有泰森多边形法、反距离加权法、趋势面法、样条函数法、普通克里格和协同克里格等几种[2,5]。其中,基于地统计理论的克里格插值方法与基于数学统计理论的薄盘光滑样条函数法又由于在插值中不需要其它先验知识与物理过程,仅仅将空间分布作为观测数据的函数,能提高插值精度且复杂度适中,因此该两种方法最适合用于空间气象要素的插值[6]。Hutchinson和刘志红等学者都针对气象要素使用薄盘光滑样条函数法来进行空间插值,并获得了较好的效果[5-14]。此外,他们还通过与其他插值方法的比较,证明了在数据密度较低的条件下,用薄盘样条函数对气象要素插值的应用前景更为广阔[5-14]。
ANUSPLIN是由澳大利亚学者Hutchinson与其同事基于薄盘光滑样条函数理论编写的专用于气候要素空间插值的程序。本文在充分了解该软件的基础上,对青藏高原地区2008年的基本逐月气象要素(气温、降水等)进行插值,并以1、4、7、10月为代表,通过变化插值变量组合来建立不同统计模型,选取研究区气温和降水插值最优的变量组合,从而提高插值精度,获得青藏高原地区较为精确的气温与降水的空间分布状况。
2 ANUSPLIN介绍
ANUSPLIN是一个专门针对气候数据、兼顾准确性、方便性与时间序列性的系统代表。ANUSPLIN允许引进多元协变量线性子模型,并可根据数据自动确定模型系数,因此该软件能够平稳地处理二维以上的多维样条函数,为气象要素空间插值引入多个影响因子作为协变量提供了可能,更重要的是它能同时进行多个表面的空间插值,对于时间序列的气象数据尤其适合[11]。
2.1 插值算法介绍
ANUSPLIN基于普通薄盘和局部薄盘样条函数插值理论进行插值。局部薄盘光滑样条函数(Partial thin plate smoothing splines)是对薄盘光滑样条函数原型的扩展[11],它除普通的样条自变量外,允许引入线性协变量子模型,如温度和海拔之间的关系、降水和海岸线之间的关系等。局部薄盘光滑样条的理论统计模型[8-9,11]表述如下:
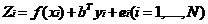 (1)
(1)
其中,Zi是位于空间i点的因变量;xi为d维样条独立变量,f是要拟合的关于xi的未知光滑函数;yi为p维独立协变量;b为yi的p维系数;ei为具有期望值为0且方差为wiσ2的自变量随机误差,wi是作为权重的已知局部相对变异系数,σ2为方差误差,在所有数据点上为常数,但通常未知[15-16]。
由式(1)可见,当式中缺少第二项,即没有协变量(p=0)时,模型简化为薄盘光滑样条原型;当缺少第一项独立自变量时,模型变为多元线性回归(ANUSPLIN中不允许该情况出现)。事实上薄盘样条函数可以理解为广义的标准多变量线性回归模型,只不过其参数是用一个合适的非参数化光滑函数代替[11]。
在公式中,函数f和系数b通过最小二乘估计来确定:
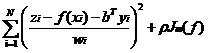 (2)
(2)
其中,Jm(f)是函数f(xi)的粗糙度测度函数,定义为函数f的m阶偏导(在ANUSPLIN中称为样条次数,也叫糙度次数),ρ是正的光滑参数,在数据保真度与曲面的粗糙度之间起平衡作用,通常由广义交叉验证GCV(generalized cross validation)的最小化来确定,也可以用最大似然法GML(Generalised max likelood)或期望真实平方误差MSE(expected true square error)最小化确定[11]。GCV计算可采用“one point move”方法,依次移去一个样点,用剩余样点在一定的光滑参数下进行曲面拟合得到该点的估测值,再计算观测值与估测值的方差。ANUSPLIN中同时提供了GCV和GML两种选择平滑参数的判断方法。
2.2 参数率定
ANUSPLIN软件由FORTRAN语言编写,包括8 个模块程序。在本次研究中,我们根据需求,主要使用了其中两个重要模块SPLINA和LAPGRD来进行研究。
SPLINA在使用时,适用于具有任意个独立变量或多个协变量的薄盘样条函数,要求插值使用的已知站点数量小于2000。其输入文件需根据插值需求,按一定顺序排列,以ASCII文件格式进行输入,本文中的研究文件包括了台站号、经度、纬度、高程及对应因变量等几个因素。软件运行时,在该模块中,有多个参数可供选择,用于建立不同组合来进行插值,从而影响插值效果。本研究中,我们主要修改了插值时的样条次数参数、自变量转换参数、协变量转换参数来进行组合,通过插值结果的精度分析来寻找最优拟合组合。使用SPLINA插值后,可以输出有关统计分析、误差分析、数据错误检测等多种信息的5—6种文件,其中最重要的为.sur文件 和.cov文件。.sur文件存储了生成的拟合表面系数,.cov文件存储了误差协方差矩阵,这两个文件都将用于后续程序LAPGRD拟合曲面数值和预测标准误差计算,是生成插值曲面图及其预测标准误差图的必须过程文件。
剩余内容已隐藏,请支付后下载全文,论文总字数:27002字
相关图片展示:
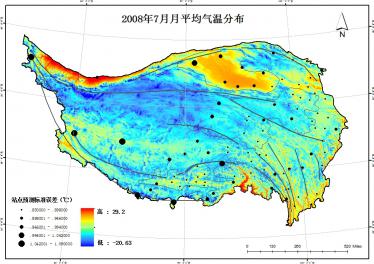
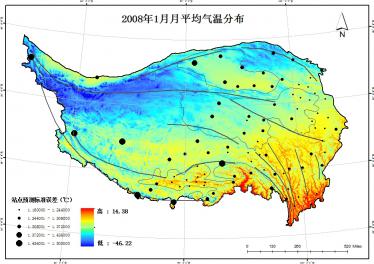
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


