论文总字数：22559字

目 录

1.绪论 1

1.1研究背景 1

1.2研究意义 1

1.3国内外研究现状 3

1.3.1模糊群体决策方法 3

1.3.2模糊共识群体决策方法 4

1.4研究内容 5

2.区间模糊共识决策方法 6

2.1问题描述 6

2.2决策流程图 7

3.实验以及分析 7

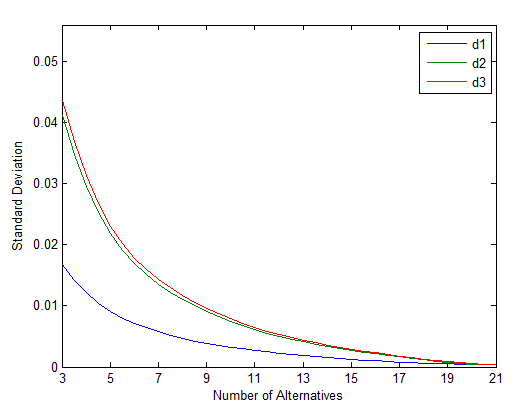
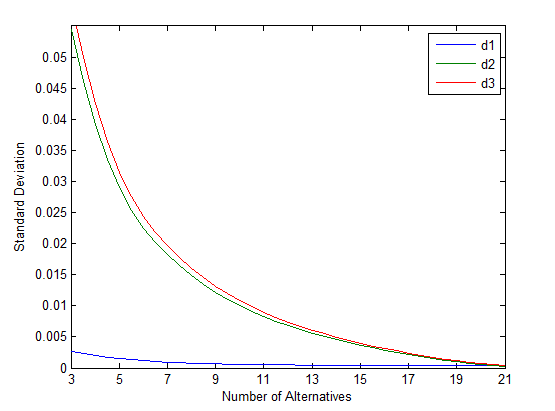
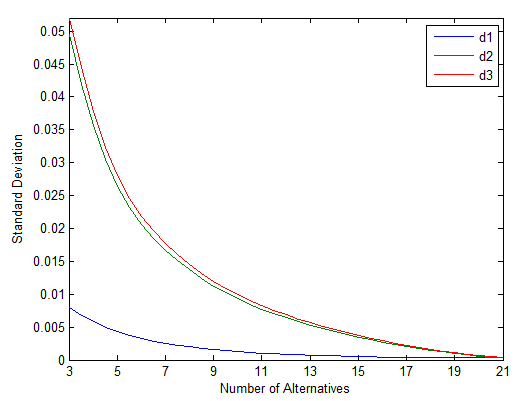
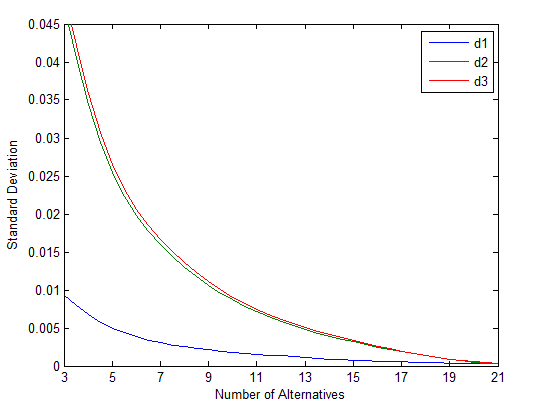
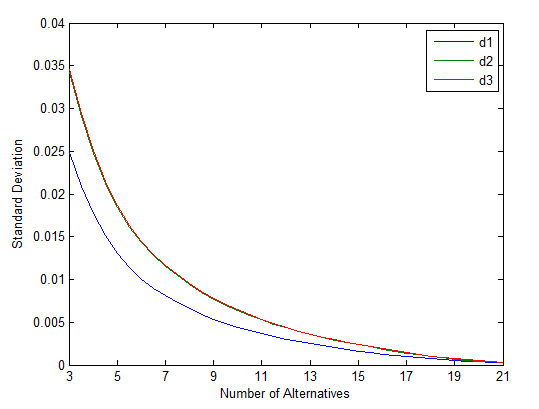
3.1不同距离公式所得排序结果的区分度 7

3.2实验结果 9

3.3实验结论的理论分析 15

4.总结 16

参考文献： 16

致谢 19

附录 20

区间模糊共识决策模型及实验分析研究

张莉莉

, China

Abstract：Research the problem of consensus decision making under interval fuzzy sets,use the simulation experiment to get random interval numbers decision matrix,get group opinion by certain methods,calculate distance between individual opinion and group opinion with different distance formulas.Then,calculate the paste progress of distance formulas with standard deviation,analyze a lot of data in order to exclude contingency of experiment.This text modells it,then make analytical investigation with MATLAB,the result is that p-fanshu formula is the best one.This text provides solving ideas for the problem of consensus decision making under interval fuzzy sets.

Key words:Interval consensus,fuzzy,consensus decision making,consensus model,simulation experiment,standard deviation

1.绪论

1.1研究背景

群体决策产生于200多年前，并在数学、经济学、行为学、心理学、信息科学等学科的基础上形成了自己的理论与研究体系，成为现代决策理论的举足轻重的一部分^[1]。“决策是管理的心脏，管理是由一系列决策组成的，管理就是决策。”这是管理学大师西蒙^[2]对决策的定义。从这句定义中，可以看出决策在管理学中的重要位置。其实不仅在管理学中，在人类的生产活动中，决策问题也有很多，特别是共识决策比如国际气候谈判、领导人选举、重要国际事项决策等，还有拆迁补偿、方案协商，商业谈判等问题。

在全球化的后现代社会中，科技发展日新月异，生活中越来越多价值与观念的冲突，都对决策过程中共识的达成提出了现实的要求，共识（consensus）与共识构建（consensus building）成为了决策领域的重要议题。就我国的具体情况来，进入社会转型期以来，由改革开放所引发的利益关系逐渐分化，利益诉求交织复杂，我国已经进入了利益矛盾和冲突的多发期。就上述的拆迁问题而言，当今社会出现的暴力拆迁与“钉子户”屡见不鲜，最后演变成社会冲突，给社会秩序和发展带来了很消极的影响。为什么分歧的偏好没有在群体决策过程中得以合理集结得到共识？又是什么导致社会矛盾的升级而不是消减？显然，主要是因为没有找到一个最佳的集结方法。尤其是在决策者给出的判断为模糊意见时，即决策者的判断为一个区间值而非具体数值时，更缺乏一种有效的集结方式主要是最佳的区间距离公式来达成共识决策。共识决策问题是近年来学术界的关注热点。在日常生活以及经济管理与政治领域中，人们都会遇到各种不同的判断决策情况，达成被一般人所接受的群体共识，但是因为每个人受教育程度，社会经历和想法不同，对同一问题便会产生不同的看法和理解，所以会做出不同甚至相反的决策结果。为了解决上述问题，本文将在借鉴相关理论的基础之上，从模糊区间的角度上审视共识决策的过程，探索专家参与决策过程中促使偏好由分歧冲突走向收敛整合的机制，促进专家群体决策过程的深度融合，提升专家意见的有效性和共识水平。

1.2研究意义

群体决策的目的是对决策议题、热点问题和重要行动展开充分讨论，达成一定程度的共识。在人们的生产生活中总会面临着多个解决方案，在众多解决方案中找出最优的解决方案是必要的。决策就是通过模式化的科学量化与计算，得到准确的判断和决策，从而创造最大的价值。在实际的决策中，决策者的判断很多情况下是模糊的区间数，为了获得最优的决策结果，决策时需要对每个个体决策者的区间数进行集结。例如，一个公司的管理层对提出的一个方案进行评估打分，不同的参与者打分均为区间数，对所得的区间分数按照一定的权重集结即得到群体意见。传统的群体决策通常忽略个体意见与群体意见之间的差异程度，简单的将个体意见进行一次性集结便得到群体意见。传统群决策过程如图1所示。

择优过程

集结过程

决策主体

决策问题 决策意见 群体意见

图1 传统群决策过程

在如上图所示的决策结果中，很容易得出偏离实际的群体意见，执行阻滞造成很高的决策成本。这种传统的决策方式引起了社会各界的关注和反思：如何使与群体意见偏差很大的个体意见在决策过程中得以修整走向收敛，决策者在实践过程中便引入共识过程参与决策。

区别于传统的群体决策，共识决策先判断个体专家意见的共识水平，若共识水平达到既定的要求时，集结个体意见形成群体意见。若共识水平没有达到既定的要求，则对相应偏差较大的个体意见进行修整，直到达成满足要求的共识水平。共识决策具体过程如下图所示。

协调者

集结意见

决策主体

决策问题 决策意见

共识测度

共识控制

择优过程

是

否

意见调整

共识过程

图2 共识决策过程

研究区间模糊共识决策有很大意义，它为专家参与有效性的理论反思提供另一种视角。基于不同理论视角的研究都将问题归结于利益诉求的表达，在选用哪些专家对问题进行决策时，参与结构的开放性会影响参与结构的有效性。是因为专家们不同学历水平、权利地位而不同的权重使决策过程不能达成共识，参与决策的过程会因为无法协调的矛盾而走向失败。这引起了我们对决策结构的反思，对共识决策形成的机理的探索将为决策结构的反思提供另一种可能。在研究共识决策的过程中，我们综合了关于共识研究和模糊研究的相关成果，涉及多个学科。在本文的研究中，涉及到了MATLAB、管理学、经济学等学科，有助于推动共识构建理论与实践的发展。一般情况下，共识决策的达成需要不断修改多个专家的初始意见并使之趋于一致，在对专家意见进行集结的时候由于利用不同的距离共识得到的共识的程度不同，寻找适合一个群体决策的距离公式在计算共识水平是群体决策的关键一步，如何选择最佳距离公式专从而得到最佳的群体共识目标往往是人们所关注的焦点问题，这也是本文所研究的内容，即研究群体集结时的距离公式具有重要的意义。尽管共识决策已经得到了很大的发展，但仍有一些点需要深入研究完善。在中外的研究成果中，大都涉及共识决策的方法以及如何进行最优决策的问题。往往较少研究当决策值是模糊区间的时的共识决策问题，本文研究的主要内容是比较不同的距离公式的区间模糊共识决策模型以及对其用MATLAB进行实验分析，最后得出最佳的距离公式。

1.3国内外研究现状

1.3.1模糊群体决策方法

群体决策是多个专家对所有方案进行打分，使用相应的决策方法对方案做出比较合理的决策，群体决策广泛应用于管理、经济、军事等领域，如质量评估、项目招标等，在学术界有着举足轻重的地位，尤其是当一些研究人员在群体决策过程中引入区间模糊理论之后，模糊群体决策中使用不同的模糊语言偏好表示集结后将得到不同的决策结果，经过万千学者的努力，模糊群体决策问题在理论研究和方法应用方面都取得了丰硕的研究成果。

Hojjat Mianabadi（2009）提出群体决策(GDM)是用来解决决策问题的重要方法之一，提出了一种模糊群体决策算法：在聚合决策者观点时，利用有序加权平均(OWA)算子来聚合个体决策者的意见，并测量和评估群体和个人观点的差距。刘芳（2013）提出模糊数互反和互补判断矩阵的一致性定义并详细地证明了相关的一些性质，给出了区间数互反和互补判断矩阵的两类转化关系，基于一致性理论和最优化思想建立了残缺区间数互补和互反判断矩阵的残缺信息估计模型。针对集成算子，特别提出了确定相关算子权重向量的确定方法。东华大学的张细香（2009）提出模糊语言偏好的表示有多种:区间数、三角模糊数、梯形模糊数、语言标度、二元语义等。她对模糊语言偏好的表示方法、模糊判断矩阵的一致性判定、不完全信息决策、群体决策中决策权的分配与个体意见集结等方面进行研究。在对次序一致性判断方法的文献分析基础上,提出了基于二元关系传递性的模糊判断矩阵次序一致性判断和修正指导方法。完善了模糊群体决策的理论研究。以上都是对模糊群体决策的静态研究，白瑞瑞（2015）提出动态模糊逻辑(DFL)群体决策模型，利用模型中提供的规则函数将五种常用偏好表达形式，即:1)效用值；2)偏好序；3)互反偏好关系；4)模糊偏好关系；5)语言评价信息，统一规划为动态模糊偏好表达，把动态研究引入模糊群体决策研究过程，拓展了模糊群体决策的研究范围。

基于以上理论分析，很多学者也在各自的领域把理论应用于实践。张云龙等人（2011）针对应急决策中许多信息无法定量描述的问题,运用模糊集合理论,建立了在事故灾难复杂环境下对应急决策进行动态调整的模糊群体决策方法。该方法包括构造模糊偏好关系、设计备选方案选择的多属性群体决策模型和群体决策一致性的检验标准等内容，可以辅助应急决策者选择最佳决策方案。刘伟佳等人（2012）提出了一种采用直觉模糊距离对黑启动群体决策结果一致性进行分析的方法。为了改善黑启动群体决策意见的一致性，每轮决策过后，对指标权重和专家权重进行调整并代入下一轮决策,直至达到满意的一致性为止。最后，用一个算例说明了所提出的一致性分析与优化方法的基本特征。

虽然理论分析和实践成果丰硕，但还是有人认为不可能达成绝对共识。比如Ron Chi-Wai Kwok（2012）提出群决策共识的不可能定理，不可能的原因是一个群体决策的结果永远不可能满足所有决策者的个人偏好。在决策过程中，为了适应个体决策者的偏好，他提出了一种模糊多人多准则决策(MMCDM)模型和一个结构化的组织决策过程。模糊多人多准则决策（MMCDM）模型包括模糊的个人偏好和群体偏好聚合。在实际操作的过程中，不仅达成共识比较麻烦，个人偏好等信息也可能失真。Gao（2013）在群体决策问题中，提出决策者的偏好信息不完整是由于人力资源质量的因素和环境的影响，决策者可以获得的信息却丢失或模糊。在前人大量理论分析和实践验证的基础上，开始有学者研究开发相关技术，来方便后人研究模糊群体决策问题。其中Syibrah Naim（2012）研究多标准决策(指标)问题，并致力于开发有能力做出决策和解决复杂问题的相关技术。在群体决策系统中，群体决策(GDM)需要考虑一组专家的意见受到语言不确定性的影响，该作者研发的区间二型模糊逻辑系统就是用来处理语言不确定性群体决策的系统。Syibrah Naim还开发出一个混合区间二型模糊逻辑与仿射的多准则群决策(MCGDM)系统。该系统模型还只是群决策过程最初的变化表现出不同的决策者的意见。

1.3.2模糊共识群体决策方法

Palomares 等（2014）将共识测度分为两大类：个体偏好与群偏好之间的共识测度、个体偏好之间的共识测度。Sun 和 Ma（2015）利用相似度概念给出共识测度，考察个体语言偏好和群偏好之间的共识水平，并将共识方法应用于多属性群决策。Xu 等（2013）提出基于距离的模糊偏好关系共识模型，同时考虑个体与群体之间的共识指标（ICI）和群体共识指标（GCI），给出迭代共识达成算法，并将该模型及算法扩展解决乘性偏好关系共识问题。Jiang 等（2013）利用兼容性测度衡量个体直觉乘性偏好与群体偏好之间的共识水平，提出了群体共识检测、达成和修正的直觉乘性偏好共识模型。Zhang 等（2014）针对直觉模糊多准则群决策问题，利用相似度公式计算个体偏好与群体偏好之间的共识水平，提出了共识参与式直觉群体决策方法。Wu 等（2015）研究了基于信任估计和集结方法的多准则群决策可视共识模型，提出了社会群体网络下的共识构建理论框架。Khorshid（2010）基于专家两两之间相似度构建正、负一致矩阵，计算各方案的正、负相对一致性，提出基于正、负理想度的语言共识测度；Chen 等（2011）针对不确定语言偏好群决策问题，利用偏差测度与重叠测度的线性组合确定专家之间的相似度，从而给出基于相似度的新共识测度定义。Wu（2014）则利用信任度及相似度的线性组合测量共识水平，给出了基于社会网络分析的区间互反偏好信任-共识模型；Pérez 等（2014）利用相似度公式测度专家模糊偏好两两之间的共识水平，提出了求解异质群体共识的决策框架；Liang 等（2016）研究了基于动态有界置信度的区间意见动力学系统，利用专家区间意见之间的 Euclidean 距离构建共识测度，分析共识或者分化形成的充分条件，另外通过仿真实验研究了动态有界置信度和区间宽度对意见动力学系统的影响，最后举例说明了该文构建的模型与原有相关模型之间的不同；Zhang 和 Xu（2015）利用优势关系表达共识指数，以此衡量个体偏好两两之间的共识水平，研究了区间直觉模糊多属性群决策问题。

基于上述对于模糊共识决策理论研究现状的分析，下面介绍模糊共识决策在实践方面的研究现状：Li（2014）提出共识决策服务在不同的物联网边缘节点信息可能不足或超负荷，如果用统计方法试图解决这个矛盾,便可以得到足够的信息提高结果可信度。他论文中首先讨论通过最小化多参数相关的匹配值的情况下物联网的服务组合。随后，提出了一种基于集群的分布式算法，共识是首先在本地计算,随后结合以迭代方式达成决策共识。分布式方法提高了可信赖的共识决策过程。Liu（2012）考虑共识决策两种情况：一种领导人和系统与两种不同的领导人。针对系统与一种领导人，我们将提供必要条件和充分条件的比例领导人预期共识。文章提出对于一个系统提供一个必要条件和一个充分条件共识决策。Gong（2012）探讨基于最小成本和最大共识问题的非编程模型。主要问题是基于最小成本的一个线性规划模型，其对偶问题是基于达成共识的最大回报的一个线性编程。通过使用双线性规划理论，不仅考虑最小成本，还探索了单位成本之间的关系。Palomares 在（2013）提出在群体决策过程中达成共识由一群决策者共同决定。不同的共识模型提出了不同作者在文献中促进达成共识的过程。Palomares提出一种适合管理决策者的共识模型，这结合了模糊决策方案来检测和管理个人和小组合作的行为。Zhang（2014）指出在共识的达成过程中(CRP)，不同的决策者将关注不同的选择。因此，决策者将自然地使用个人共识方法来衡量个人的共识度。同时，很难设置阈值来判断共识达成共识程度是否可以接受。为了发展个人共识方法和避免设置阈值的共识，他的文章研究提出了一种新颖的满足群体决策(GDM)的共识模型。

1.4研究内容

本文主要分为三个部分，主要研究内容如下：

剩余内容已隐藏，请支付后下载全文，论文总字数：22559字

相关图片展示：