多尺度多频率多极化海面微波散射数值模拟

论文总字数：29533字

目 录

1引言1

2国内外现状1

3海面微波散射模型2

3.1 多尺度模型2

3.2 主被动协同（主动）模型4

3.3 复合表面布拉格模型5

4 海面粗糙度谱6

4.1 Donelan‐Banner‐Plant谱7

4.2 Elfouhaily谱8

4.2.1 长波曲率谱9

4.2.2 短波曲率谱9

4.3 Hwang谱10

5 海面微波后向散射的模拟与验证12

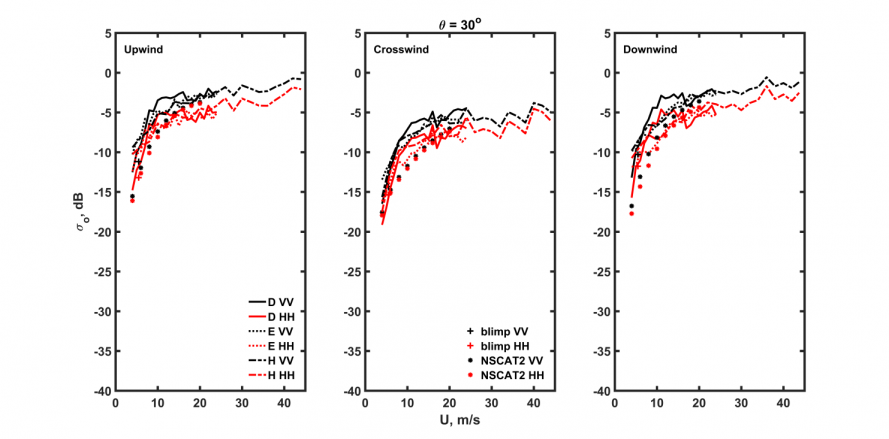
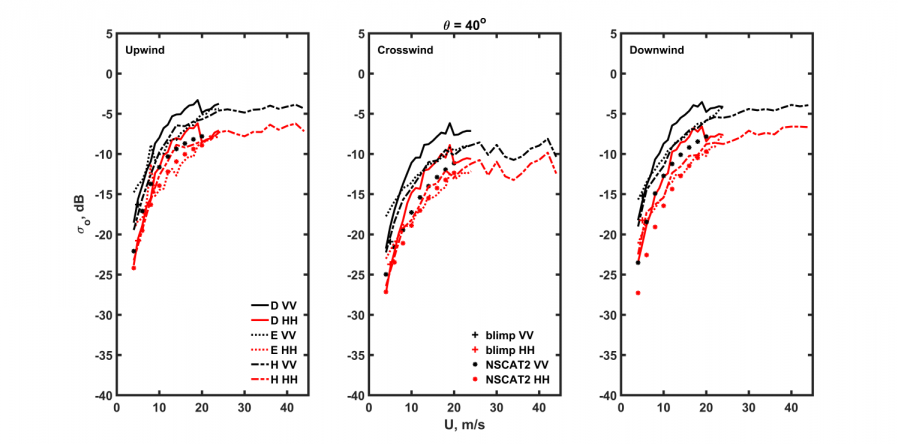
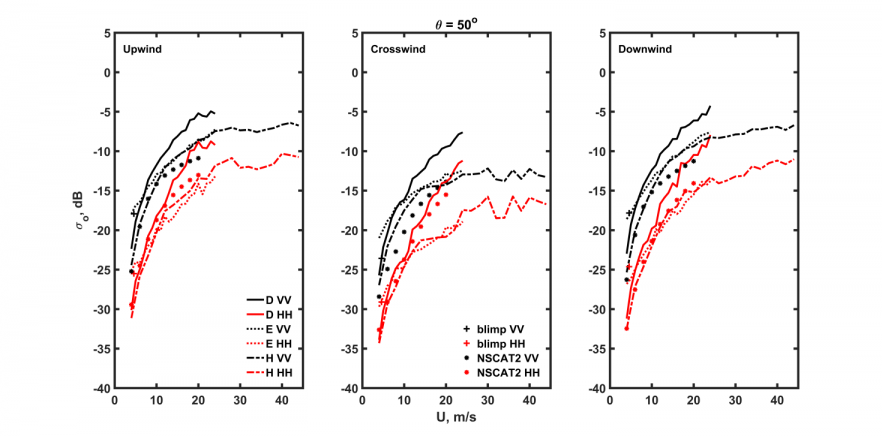
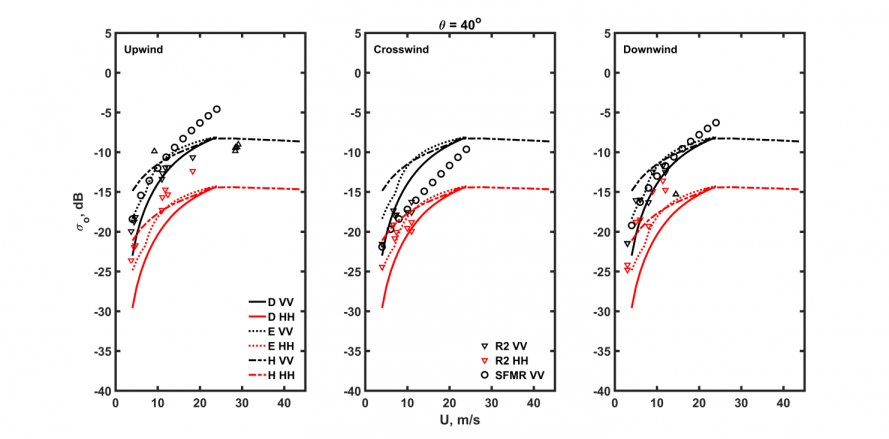
5.1 全极化下的风速依赖性14

5.2 Ku、C和L波段的比较18

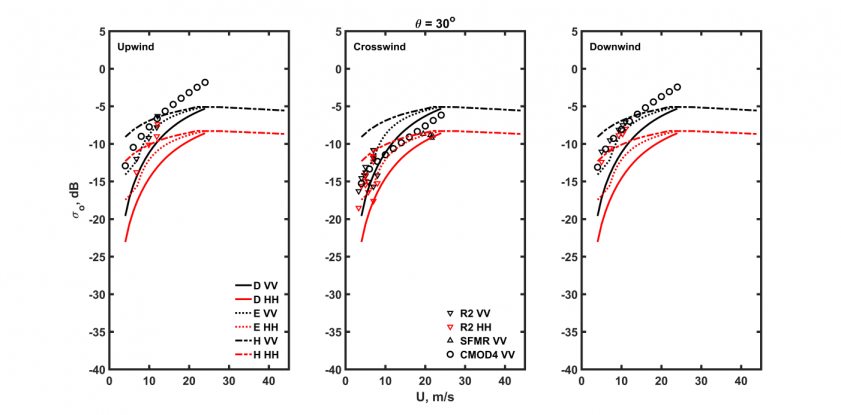
5.3 验证20

6 总结与讨论22

参考文献23

致谢25

多尺度多频率多极化海面微波散射数值模拟

赵晓露

，China

Abstract：The popular view of microwave backscatter from the ocean surface are composite surface and quasi-specular theories, and it is necessary to take multiple scattering related with Kirchhoff integral into account at scattering process in recent years. Co-polarization normalized radar cross section has been explained well by Bragg/composite surface scattering at moderate incidence angle. We investigate the predictions of normalized radar cross section form sea surface at moderate incidence angle with wind speed varying from low to high through using different scattering models with three spectrum functions, and find it depends on wind speed, incidence angle, radar frequency and azimuth angle by the explicit way. We also present in-site measurements and geophysical model functions for radar backscatter from 0 to 58 m/s at Ku, C and L bands. In general, VV-polarization NRCS measurements were better explained by the scattering models than the HH polarization, and the Ku band is more sensitive to the selection of roughness spectrum than the C and L bands. The results of inversion of co-polarization backscatter using the CB model with E spectrum at moderate incidence angle and low and moderate wind speeds are the best, and the CB model with H spectrum is better for cross-polarization than with D and E spectrum.

Key words: backscatter; NRCS; roughness spectrum

1 引言

来自海洋表面的雷达后向散射已经被非常有效地用于全球风速反演。这种成功应用揭示了雷达散射和海面粗糙度密切相关，同样与后向散射相关的风生波也占据着主导地位。对海面雷达后向散射的理论研究有着悠久的历史，近些年许多逼真活跃的识别海面特征的物理模型被提出，然而人们认识到使用这些模型都很难在大范围的入射角、风速、雷达频率以及变化的风浪场和不同极化状态下获得对归一化雷达横截面（NRCS或）的一致性描述。因此在科技发展的基础上加强学习理论知识的重要性不言而喻，对于海洋遥感进一步认知不同尺度的表面波特性也是十分关键的。

大约半个世纪前短表面波的布拉格共振已经被确定为水面雷达后向散射的重要机制，这些短波被较长的波浪倾斜和调制。最近Plant在遵循复合表面理论的基础上打破仅由自由传播的风产生的波（自由波），还包括轻微破碎的波（边界波）和更强烈的破碎深水波（破碎波）。在第二节中，我们将简单阐述本文使用的海面微波散射模型，包括Plant [2002]的随机多尺度模型；Plant等 [2017]的主被动协同模型，因为本文主要讨论雷达横截面，所以使用的是其中的主动散射计模型；和Valenzuela等 [1978]的复合表面布拉格（CB）散射模型。

使用三种不同的物理模型，将谱函数[Donelan-Banner-Plant，2002；Elfouhaily等，1997；Hwang，2013]作为计算NRCS值的输入，这将在第三节中阐述。第四节介绍来自三个谱模型的海面粗糙度谱，为了方便，将它们称为D（Donelan-Banner-Plant）谱、E（Elfouhaily等）谱和H（Hwang）谱，前两者涉及波长从毫米延伸到约300米，后者的波数范围从31rad/m覆盖到508rad/m并且将风速应用范围扩展到强风。模拟结果将和不同波段的数据集进行比较，Ku波段(14GHz)，飞艇数据[Plant等，1998]和NSCAT2模型函数[Jones等，1997]，C波段(5.4 GHz)，RADARSAT-2（R2）和步进频率微波辐射计（SFMR）全极化NRCS产品与来自国家数据浮标中心（NDBC）海上浮标原位风测量的结果，以及C波段地球物理模型函数（CMOD4，Stoffelen和Anderson [1997]），L波段(1.26 GHz)，水瓶座数据[Yueh等2014]，第五节中将呈现海面微波后向散射的模拟和验证。第六节是总结与讨论。

2 国内外现状

从海洋表面开发微波后向散射物理模型的依据大都是准镜面散射、布拉格散射和复合表面理论。中等入射角下的后向散射来自自由短表面波的布拉格散射，小入射角时散射过程变为准镜面，近几年水面微波散射理论的发展表明散射过程中还需要考虑与基尔霍夫积分相关的多重散射。期间的理论和实验数据表明，共极化后向散射风速反演在高风况下对入射角和方位角趋于饱和和衰减，但最近分析表明交叉极化的雷达后向散射在高风速中不发生饱和。

基于这些理论已经开发出来了许多优良的海面微波后向散射模型，包括随机多尺度模型、主被动协同（主动）模型和复合表面布拉格模型；以及Romeiser等 [1997]通过在二维表面斜率上泰勒展开NRCS，近似得到布拉格散射面的几何和流体动力学调制，提出了基于物理原理的改进复合表面模型；Donelan和Pierson [1987]将详细的参数作为输入，提出了包含重力-毛细波的复合表面模型；Kudryavtsev等 [2003]使用短风波谱和波浪破碎统计对海面进行描述，开发了一种考虑布拉格机制和与破碎波相关的非布拉格散射机制的半经验物理模型。

对于广泛分布的波数范围，Plant等 [2002]将连续表面分为小、中和大尺度波浪的区域。大尺度波高对应长波，其波数低于人为选择的截止波数；中尺度波对应中等波数，其波长基于参数入射辐射波数和表面均方根高度的乘积获得；小尺度波高对应该参数的小值和小波数。不同尺度的波在各自波数范围内获得频谱，并将较大尺度波的表面斜率用于对较小尺度波的调制。于是小尺度波在倾斜的中尺度面上计算布拉格散射，位于中等波数的布拉格波在大尺度面上数值求解基尔霍夫积分。对不同尺度的波先单独计算NRCS，再平均产生平均雷达横截面。多尺度模型的优势在于通过尺度分解并使用基尔霍夫积分方法可以很好地预测中低风速下中等入射角的,而不需要有效的反射系数。但这也为风速依赖性带来了很大的不稳定，在模型中考虑多重散射和破碎波或许能减小这种不稳定性。

为了进一步改善多尺度模型，Plant等 [2017]表明如果海洋辐射计和散射计微波识别物理模型中包含边界波和破碎波，单波谱可以解释辐射亮温和NRCS两者的合理精度，尤其是在高入射角下增大值。基于早期工作，Plant使用母波的斜率概率分布的附加信息对边界波建模。破碎波和泡沫建模都建立在Phillips [1985]引入的函数上，该函数描述了以速度行进的破碎区域单位面积的平均峰值长度。为此通过修改标准方向波谱和风力变率来使计算过程中包含边界波和破碎波。加入边界波和破碎波效应后，主被动协同（主动）模型提高了VV极化下雷达横截面与观测量的一致，但对HH极化的预测似乎没有起到很好地改善。为了探究的这种行为，也许我们应该考虑涌浪或者其他因素的作用。

通常认为在中等入射角和风速的情况下，海面微波散射由布拉格散射主导[Valenzuela，1978]。这是因为雷达发射的电磁波与布拉格波，其波长与电磁波相当，发生共振。海洋中布拉格共振中的短波被复合表面布拉格（CB）理论所描述的长波倾斜。已经由实验数据证明归一化雷达横截面与布拉格波的波高谱密度成比例。另一方面，我们知道只用纯布拉格散射理论很难模拟观测到的NRCS值。复合表面布拉格散射模型能够很好地重现共极化雷达横截面，但是因为没有包含布拉格散射的二阶贡献而无法合理解释交叉极化（VH或HV，垂直发射水平接收或水平发射垂直接收）横截面，不过这个问题已经通过二阶小斜率近似模型得到解决。

3 海面微波散射模型

3.1 多尺度模型

用于海面后向散射的归一化雷达横截面的基础是

(1)

其中和是入射平面内和垂直于入射平面的滞后距离，是雷达波数，是入射角，q和p表示极化方式，由

(2)

和

(3)

分别给出VV和HH极化（VV是指垂直发射垂直接收，HH是指水平发射水平接收）。是相关介电常数。当统计是高斯分布的，是表面波高的均方根和是表面高度的自相关函数。

剩余内容已隐藏，请支付后下载全文，论文总字数：29533字

相关图片展示：