论文总字数：16512字

摘 要

随着全球金融市场的发展，学术界对金融市场中风险的度量及其控制方法越发的关注。本文主要是探究欧洲主权债务危机期间美国债券市场的波动性及其变化的情况。传统的风险度量方法以马可维茨所提出的方差法为代表，除此之外还有敏感度方法、失真函数法、波动性方法、一致性度量风险方法、VaR方法等等。但这些传统的度量方法在各自的某些方面均体现了内在的局限性。而本文从一个较新的方向即主要运信息熵，同时配合使用香农熵的值的变化特征和内涵来进行研究分析。文中主要通过对巴克莱美国综合债券指数的处理和分析，结果发现指数所对应的信息熵熵值的变化可以反映债券市场的波动性情况。

【Abstract】With the development of the international financial market, academia has paid more attention to the measure and management of volatility of financial market. In this paper，we are going to study the variance of the US bond market during the period of European sovereign debt crisis. Traditional measuring methods involve Markowitz’s Mean-variance Method, Sensitivity-based Method, rate–distortion function, Consistency of Financial Risk Measurement Methods, VaR Method and so on. However, these traditional methods have some limitations inevitably. Thus, in this paper, a comparatively new aspect, entropy, will be introduced. In the meantime, the entropy with the variation and content of the value will be used. With the analysis of the AGG index, the change of the entropy corresponding the index cans reflect the volatility of the bond market.

【关键词】标度不变性 扩散熵 欧债危机

目录

摘要 I

第1章 绪论 1

1.1研究背景与意义 1

1.2文献综述 1

1.3研究内容与框架 3

第2章 理论基础与研究模型方法 5

2.1理论基础 5

2.2研究方法构建 8

2.2.1扩散熵分析算法（DEA）： 8

2.2.2分析算法的改进与完善 10

第3章 实证分析与研究 12

3.1数据 12

3.2实证研究 14

3.2.1标度不变性 15

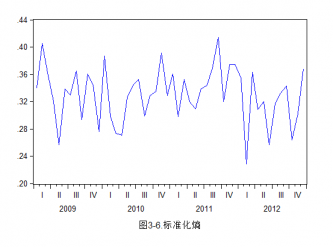
3.2.2.标准化熵 17

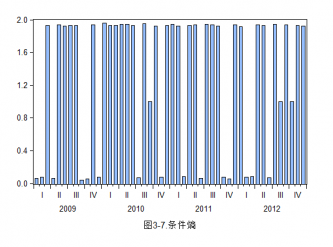
3.2.3条件熵 19

第4章 结论 21

致谢 22

参考文献 22

第1章 绪论

1.1研究背景与意义

随着国际金融市场和国际金融体系的不断健全和发展，近年来开始从不同角度关注金融市场波动及其风险的学者越来越多。而目前金融市场的波动情况一般通过投资组合的收益的标准差或方差的值的大小来衡量，其中标准差或者方差则是用于表示投资组合的风险大小。现如今关于股票、债券市场波动情况的研究是相对不充分的。在受到近十几年来大量涉及股票或衍生工具的金融性危机的教训启发之后，关于金融风险的测量和管理技术有了快速的发展。其中，通过对金融时间序列的分析方法更多地得到研究学者们的关注。

债券市场是金融市场中极其重要的一个组成部分，它的波动程度即稳定性情况对一国宏观经济产生重大的影响。而在现如今经济全球化不可逆的趋势下，债券市场的运行的好坏也将直接关系到世界经济的发展。而克劳德·艾尔伍德·香农把物理学中熵的概念引入了信息论后，可以用熵表示不确定性的程度。由此，利用信息熵方法来探究债券市场的运行情况以及预测经济形势未失为一种展新的思路。

1.2文献综述

对于信息熵这个较为新颖的概念，有许多研究者曾经在各自的研究中提出自己对其的认识和理解。Gao和Hu（2013）认为现有的提前预警系统（EWS模型）运用的是一种汇总变量，这种变量不能进行在不稳定、不均衡经济中规模小于一个国家的参与者的非线性动态研究。为了帮助弄清楚金融危机的机制以及为金融危机和经济衰退定义新的稳健性指标，他们使用“解剖”的方法，即分开测量一个经济体中不同部分的收入结构，同时也去分析与房利美/房地美、雷曼兄弟以及美国国际集团相联系的接触网络。接触网络的损失是可以被一个双参数类大森定律分布表示地震余震的模型。这样的一种分布暗示了损失将普遍存在于危机和衰退之中。

Oha等（2015）在分析了金融市场的不稳定性的同时也分析了金融市场中极端事件的发展模式，他们的结论发现：利用信息熵方法可以预测和捕捉到金融危机的发生时间。

Gao等（2011）提出了正收益和负收益熵值及其分布分析种个度量方式，用于研究“空间”集合以及世界经济在1990至2008这十九年间九大行业的企业在时间动态上的情况。实证发现经济出现衰退时薄尾指数分布会变成拥有更高熵值的帕累托分布同时厚尾程度高于正收益的情况，该特征适用于危机爆发行业到其他行业。

Yager（2000）提出，大量不同类型的不确定性都可以在同一个框架来表示。而作者提供了一个称作熵的名堂可以用来计算与模糊测度相关联的不确定性。

Pingke和Baoding（2008）讨论与模糊变量相关的不确定性的程度。基于信誉度量的概念，熵的定义从信息理论观点配制及其性质进行了研究。最后，熵和公理化刻画的替代定义的建设被给出了一些评论。

Chen和Dai（2011）提出不确定熵的概念被用于提供与不确定变量相关的不确定性的定量测量，给出了不确定变量的熵的一些例子以及提出了不确定变量的最大熵原理，也就是所有的不确定性分布满足给定的约束条件，应选择一个最大熵。

而对于信息熵方法的应用来说，在现有的研究中采用该种方法对债券市场的研究很少，但是国内外以往的文献中利用信息熵方法来对股票市场发起研究的文章比较多，虽然研究对象有所不同，但思路和方法可以用来参考和借鉴。乔坎坤和卢志明（2013）利用了扩散熵对深圳成指、道琼斯指数、上证指数以及恒生指数最近十八年的日收盘价时间序列进行了其内在规律性的研究分析，并从结果发现发达的股票市场具有的特点是较强的内在排斥性，相邻时刻的股指的变化具有抑制作用。而国内两只股指（上证指数和深圳成指）则呈现较强的内在依赖性。

黄静静等（2013）指出当实验数据的数量在较多或较少两种情况下使用方法方法评估风险的缺点，如忽略了某些性质或产生离谱的误差等。同时提出采用对数收益率的绝对数值来衡量波动。在这个基础上采用扩散熵和推广后的Tsallis熵对不同时期的股票市场进行波动分析，同时引入标度参数和相应标度指数，结果发现股票市场的发展程度或成熟度不影响规则波动的内在相关性和极端波动的内在排斥性。

陶芮（2011）在研究中首先介绍了扩散熵方法的一个重要基础及标度不变性。标度是数理学以及天文学领域的一个概念，即概率分布函数满足标度化关系为，则认为随机变量它所表示的这个随机过程是标度的，而标度不变则是指当参数变量和发生变化如成时，概率分布函数不变即映射方式不变。在这个基础上分析了扩散熵方法及其相对于方法方法的精确性和优势。随后将这种方法运用于现实金融市场中探究了金融数据的统计特征及其标度特性。

沈文昊等（2014）主力于从金融时序数据中探究其波动的特征和规律，挖掘数据中所隐含的丰富信息。所以作者主要采用了由Approximate熵方法引申发展而得的Sample熵方法，在解决了Approximate熵方法内在的误差和局限性并提高了评估精度的同时，对国内外的四只股票指数进行了实证研究分析。分析的结果发现金融（股票）市场的短期行为更具有随机性，而中长期行为则更具有相关性。另外由于国内外的政府干预程度不同，所以各自的金融指数对现实金融事件的反应速度也有所区别：西方指数较为敏感而中国指数相对滞后。

由于不同的金融市场各自的运行特点有所不同，而金融市场间自不必说会存在着紧密的联系。王媛和李帆（2014）为了研究中国及美国的股票市场和债券市场间的相关性的问题，采用了VAR模型、方差分解等实证方法对相关股票指数和债券指数在若干年间的走势变化情况进行研究分析，结论发现无论是中国市场还是美国市场各自或相互之间，股票市场与债券市场间都存在着一定程度的“跷跷板效应”，即替代效应。

从前人的研究中可以看出，对于金融市场来说，可以从物理学范畴中引入信息熵的概念，用于刻画金融系统中不确定性的情况。而且经过实证的检验后，可以采用信息熵的方法对股票市场的稳定性情况作出一定程度的度量。然而，研究至今几乎没有使用这种方法对同样重要的债券市场进行分析。所以，针对这种情况，本文将采取扩散熵和条件熵的方法对债券市场的波动情况进行实证研究分析。

1.3研究内容与框架

针对以方差法、敏感度方法、失真函数法、波动性方法、一致性度量风险方法、VaR方法等传统风险度量方法的局限性和不足，本文决定从信息熵的角度及相应方法对金融风险进行重新认识及度量。

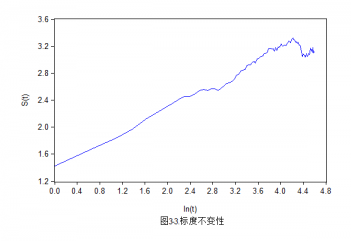
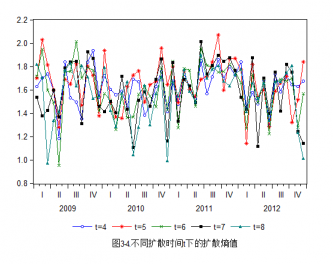
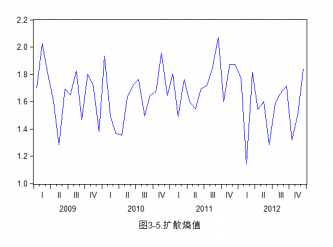
所以，本文的结构主要分为以下几个部分：第一章是上文对现如今金融市场发展过程中对风险认识的简介以及国内外金融界近段时间对信息熵应用在金融市场研究上的总结；第二章主要介绍关于信息熵的理论基础以及信息熵方法与传统的金融风险度量方法尤其是方差法之间的比较；同时介绍本文所使用的扩散熵方法所用到的数据以及熵计算的数理模型、构建方法及其改进；第三章是结合巴克莱美国综合债券指数（AGG index）在2009年到2012年间的数据及其熵值与现实宏观经济中所发生的事件研究信息熵的债券指数所对应的熵值与债券市场波动性之间的关系，其中主要对其标度不变性、扩散熵、标准化熵、条件熵进行分析研究。最后第四章结合前文的研究以及实证分析对全文的简要总结。

第2章 理论基础与研究模型方法

2.1理论基础

信息熵也称香农（C.E.Shannon）熵，它虽然继承了Boltzmann熵的思想，但与此同时却融入了比后者更多的想象和创造，在另一个全新的角度上，对熵的概念做出了全新的定义。其实质性含义，即表达关于事物的不确定性的数学解释和度量。需要特别提出的是，Boltzmann熵中的不确定性并非无条件的，所以它仍然属于Clausius的物理学熵的范畴之内。而Shannon熵几乎可以认为是属于一个新的概念范畴了。但如果抛开了不可逆性过程而单单就其状态而言，Shannon用熵来描述信息源，这并不能说是一念之差。Shannon随后给出了一个可以用来取得离散的信息源所“产生”的信息量的多少的公式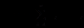：，它与Boltzmann所给出的熵的微观解释的公式的形式完全是一致的。信息上不仅可以用来计算信息量的多寡，它在实质上是一个有普遍适用性意义的关于不确定性的数学度量。Shannon将熵的概念从热力学领域引用使之引发人们对信息论的思考，这就赋予了熵更加广泛的意义和研究范畴。与此同时，这也引起了数学界对于不确定性的度量的更深一步的探索。而后来陆续出现的测度熵、拓扑熵、以及本文主要使用的扩散熵就是与Shannon熵一脉相承的。

而在金融风险度量的方面，是数理金融学科的极其重要的课题研究，与估值共同存在并横穿在金融学、经济学的各个领域研究之中。又由于风险普遍存在于金融市场之中，随着现如今国际金融市场的进一步全球化的快速发展，全球金融市场的总体风险日益加深。此时，重要的是应该如何理解风险、如何度量风险以及如何管理风险等一系列的问题。其中度量风险是关键的一环，只有准确、科学地做好风险的度量，才能有效地进行风险管理。

美国的经济学家马可维茨（Harry Markowitz）主要是采用收益率这个指标的数学期望值来度量单个资产或者资产组合的投资收益，同时用这个收益率的方差来度量单一资产或资产组合的风险大小，以此解释和建议投资者应怎样去构建出一个有效的资产组合，这也使得“均值-方差模型”成为投资者们进行投资或对投资组合进行理论上的研究及其实践操作的基础。

方差是一个特性良好而方便使用的统计量。在Markowitz的资产组合理论中，投资组合的方差被拆分成两个部分，一部分是单一资产自身的方差，另一部分则是不同的资产间收益的协方差。然而，在事实上利用方差或（标准差）的方法度量风险会出现很多问题：

第一，方差是用于衡量随机变量偏离其期望水平的程度大小的统计量。然而，这种对平均收益率的简单的偏离研究是没有太多实际含义的。因为人们通常不会将高于平均水平的收益部分归为风险，而他们所认为风险仅仅是收益低于平均水平的那部分。所以方差法并没有很好地照顾到一般投资者的主观心理。

第二，在特维斯基和卡尼曼对投资者风险心理的研究中可以发现，大多数的市场参与者对投资过程中亏损的担忧会比相同程度的盈利所带来的愉悦感觉更加强烈。借助Value Function来表示即价值曲线在参考点以下的部分（亏损）的一阶导数要大于在盈利部分中相应程度的大小。而方差法则没有区分开总体的波动性和投资过程中的风险，换句话说，高于期望水平的收益部分将意味着会增加投资组合的整体风险，显然这并不是一种符合常理的描述。

第三，方差法所假定的收益率是服从高斯分布的，然而后来的研究基本上都对这个假设持否定的态度。事实上，如果收益率的分布具有正偏的特点，方差法会高估风险程度，因为高于平均收益率的部分要比低于平均收益率的部分大，而如果收益率的分布是负偏的，方差法则会低估风险程度。

剩余内容已隐藏，请支付后下载全文，论文总字数：16512字

相关图片展示：