论文总字数：22239字

摘 要

近些年来，越来越多的研究人员将机器学习理论应用于图像分割领域，并取得很好的分割效果。根据机器学习理论，有监督学习(Supervised Learning)分类方法是基于样本点的特征，通过学习已标定样本的特征，最终得到具有特征识别能力的分类器，用于判断预测未知样本的类别。

本文主要研究基于三维Zernike矩构造的3DZD（Three-Dimensional Zernike Descriptors）特征向量的分类器训练和相关参数的优化。

首先，我们研究了支持向量机理论和随机森林理论等有监督学习算法。然后研究了分类器参数调优。我们采用了网格搜索方法对参数C和g进行调优。接着研究了对特征向量进行优化，包括两方面内容：（1）改变三维Zernike矩的阶数N以研究基于不同阶数的特征向量对分类器性能的影响；（2）利用随机森林算法选择特征向量中权值较大的特征描述子，构成新的特征向量以研究其对分类器性能的影响。最后，总结归纳分类器设计流程和参数调优、特征向量优化方法，分析可以进一步优化的方向。本文实现了对分类器参数和3DZD特征向量的优化分析，并获得血管分类器。

关键词：三维Zernike矩，特征向量，支持向量机，随机森林，参数优化

Abstract

In recent years, more and more researchers are applying the machine learning theories to image segmentation and have achieved great performance. According to the machine learning theories, supervised learning is to learn the features of the labeled samples and finally achieves the classifier with ability to recognize the features and to predict the labels of the unknown samples.

The thesis mainly studies the classifier training and related parameters optimization based on the 3DZD(Three-Dimensional Zernike Descriptors) feature vectors.

First, we research two supervised learning algorithms such as support vector machine(SVM) and random forest. Then we study the optimization of the parameters of the classifiers. Here, we use the grid search to find the best C and g. Then, we study to optimize the feature vectors, including two aspects: (1) change the order of Zernike matrix to see the influence of the length of the feature vectors on the classification, and (2) apply the random forest to compute the importance values of the features of the feature vector, and then select the features of high importance values to make new feature vectors and use the new feature vectors to train new classifiers, to test the influence on the classification accuracy. At last, we summarize the design process of the classifiers and the methods for parameter optimization and feature vector optimization, and we further analyze new potential methods for optimizations.

The thesis finally realizes the optimization of the parameters and feature vectors.

Keywords: vessel segmentation, SVM, random forest, parameter optimization, feature vector

目录

摘 要 I

Abstract II

第一章 绪论 1

1.1 课题背景 1

1.2 支持向量机和随机森林简介 1

1.3 实验数据 2

1.3.1 训练样本数据集 2

1.3.2 测试数据集 3

1.4 本文的研究目的和研究内容 3

1.5 本文组织结构 4

第二章 分类器设计 5

2.1 SVM理论及应用 5

2.1.1 SVM理论 5

2.1.2 SVM应用 7

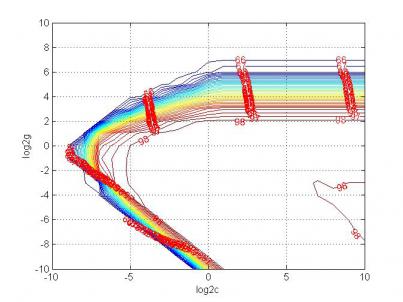
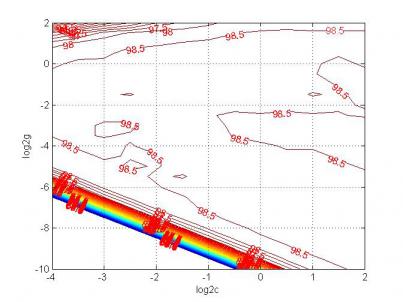
2.2 支持向量机分类器的参数优化 8

第三章 基于三维Zernike矩理论的3DZD特征向量优化方法 10

3.1 引言 10

3.2 实验设计 10

3.3 实验结果和分析 11

第四章 基于权值的3DZD特征向量优化方法 12

4.1 引言 12

4.2 实验设计 13

4.3 实验结果和分析 13

第五章 论文总结与分析 15

5.1 本文实验的分析 15

5.2 对两种优化的进一步比较 15

5.2.1 实验方法 15

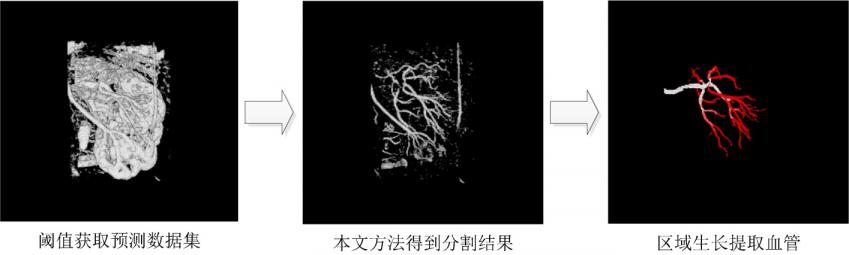
5.2.2 对6组预测图像进行分割 16

5.3 本文总结 17

5.4 展望 18

致谢 19

参考文献 20

第一章 绪论

1.1 课题背景

随着社会的发展，血管类疾病已经成为重要的公共卫生问题之一。血管分割在医学诊断中具有重要意义，是大量临床步骤的重要先决条件，对辅助诊断、治疗和手术都具有重要价值。近些年来，越来越多的研究人员将机器学习理论应用于模式识别和图像分割领域，并取得很好的效果^[11-15]。根据机器学习理论，有监督学习分类方法是基于样本点的特征，通过学习已标定样本的特征，最终得到具有特征识别能力的分类器，用于判断预测未知样本的类别，进而通过后处理实现完整分割效果。

基于机器学习方法的血管分割应用主要包括两个部分即特征向量提取和分类器训练。本文采用的特征向量数据是基于三维Zernike矩提取的体素点相关局部区域形状的3DZD特征向量。本文将重点研究分类器训练及相关参数的优化。其中，相关优化涉及到3DZD特征向量的优化以及所采用的机器学习算法相关的分类器训练参数优化。

本文提供的实验数据可靠且经过简单测试可以达到基本分割效果，由于3DZD特征向量包含的信息丰富且没有进行充分的挖掘，所以本文一方面通过三维Zernike矩理论的相关知识对3DZD特征向量进行优化，并结合不同局部区域尺寸进行分析。另一方面，通过充分利用3DZD特征向量的权值信息对构成特征向量的描述子进行取舍，保留权值较大的描述子构成优化后的3DZD特征向量，从而保证特征向量对于血管分类器的有效性。

1.2 支持向量机和随机森林简介

本文通过有监督学习算法来实现血管分类器设计，现在对其做简单的介绍。

有监督学习模式识别理论具有很成熟的应用实践基础。有监督学习是指利用一组已知类别的样本信息调整分类算法的相关参数，使其达到所要求性能的过程，也称为监督训练或有教师学习。有监督学习是从已标记的训练数据来推断一个功能的机器学习任务。训练数据包括一套训练样本。在有监督学习中，每个实例都是由一个输入对象（通常为向量）和一个期望的输出值（也称为监督信号）组成。有监督学习算法分析该训练数据，并产生一个推断功能，它可以用于映射新的实例。这需要算法以某种合适的方式从训练数据推广到未知的情形。这里主要采用两种经典的有监督学习分类算法：支持向量机和随机森林。

支持向量机(Support Vector Machine，SVM)是Corinna Cortes和Vapnik等于1995年首先提出的，它在解决小样本、非线性及高维模式识别中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中。SVM属于一般化线性分类器，是机器学习领域若干标准技术的集大成者，它集成了最大间隔超平面、Mercer核、凸二次规划、稀疏解和松弛变量等多项技术，在若干挑战性的应用中，获得了目前为止最好的性能。SVM的主要思想可以概括为两点：⑴适用于分析线性可分的情况，对于线性不可分的情况，通过使用非线性映射算法将低维输入空间中线性不可分的样本转化为高维线性可分的特征空间，从而使得在高维特征空间中采用线性算法对样本的非线性特征进行线性分析成为可能；⑵它基于结构风险最小化理论，在特征空间中构造最优分隔超平面，使得分类器达到全局最优化，并且整个样本空间的期望风险以某个概率满足一定上界。由于其具有全局最优、结构简单、推广能力强等优点，近几年得到了广泛的研究并广泛应用于模式识别等领域^[3]。

随机森林(Random Forest）是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出类别的众数(mode)而定。Leo Breiman和Adele Cutler推论出随机森林机器学习算法，而 "Random Forests" 是他们的商标。这个术语是1995年由贝尔实验室的Tin Kam Ho所提出的随机决策森林（random decision forests）而来的。这个方法则是结合Breimans的"Bootstrap aggregating"想法和Ho的"random subspace method"来构造决策树的集合。它具有很高的预测准确率，对异常值和噪声具有很好的容忍度，且不容易出现过拟合，在医学、生物信息、管理学等领域有着广泛的应用。

在机器学习中，随机森林是一种统计学习理论，是用随机的方式构造一个森林，森林由很多的决策树组成，随机森林的每一棵决策树之间是没有关联的。在得到森林之后，当有一个新的输入样本进入的时候，就让森林中的每一棵决策树分别进行一下判断，看看这个样本应该属于哪一类（对于分类算法），然后看看哪一类被选择最多，就预测这个样本为那一类。

在建立每一棵决策树的过程中，有两点需要注意：采样与完全分裂。首先是两个随机采样的过程，随机森林对输入的数据要进行行和列的采样。对于行采样，采取有放回的方式，也就是在采样得到的样本集合中，可能有重复的样本。假设输入样本为N个，那么采样的样本也为N个。这样使得在训练的时候，每一棵树的输入样本都不是全部的样本，使得相对不容易出现过拟合。然后进列采样，从M个特征中，选择m个(m lt;lt; M)。之后就是对采样之后的数据使用完全分裂的方式构造出决策树，这样决策树的某一个叶子节点要么是无法继续分裂的，要么里面的所有样本的都是指向同一个分类。一般很多的决策树算法都一个重要的步骤-剪枝，但是由于之前的两个随机采样的过程保证了随机性，所以就算不剪枝，也不会出现过拟合。

1.3 实验数据

本文所用到的实验数据是基于三维Zernike矩构造的3DZD特征向量，其相关理论和计算推导过程参见文献^[5]。

3DZD可用于描述三维空间几何特征，由于不同n和l对应的3DZD具有描述目标对象的不同几何特征信息，对于给定的N，可将所有的3DZD构成一个向量，即（F00，F11，F20，F22，…）用于表示三维空间几何形态的特征，我们将3DZD构成的向量称为3DZD特征向量。

由于n，l，m之间满足一定的约束关系，对于确定的阶数N，可以得出3DZD特征向量中包含的描述子个数L：

（1.1）

剩余内容已隐藏，请支付后下载全文，论文总字数：22239字

相关图片展示：