基于密度的聚类算法分析与实现

论文总字数：19770字

目 录

1. 引言 1

1.1 选题背景及意义 1

1.1.1 基于分层的聚类 1

1.1.2 基于划分的聚类 1

1.1.3 基于密度的聚类 2

1.1.4 基于网格的聚类 2

1.1.5 其他聚类方法 3

1.1.6 本文研究的聚类算法 3

1.2 论文结构 3

2. CFSFDP算法分析 4

2.1 CFSFDP聚类中心 4

2.1.1 局部密度 4

2.1.2 距离 5

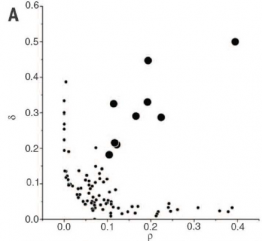
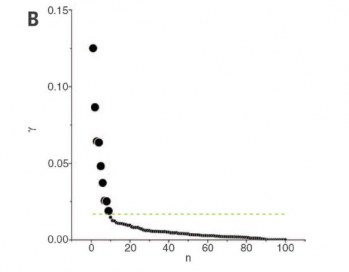
2.1.3 决策图 5

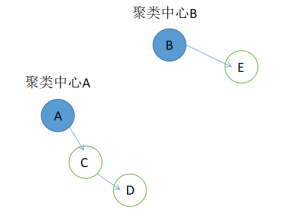
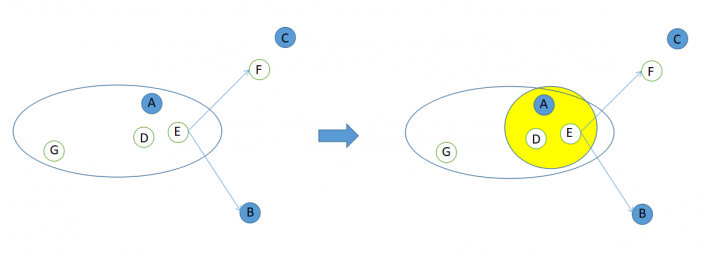
2.2 CFSFDP聚类算法 7

2.3 CFSFDP算法存在的问题 10

2.3.1 截断距离的选取 10

2.3.2 距离 11

3. 算法改进 11

3.1 信息熵的引入 11

3.2 算法的改进 12

4. 实验与分析 13

4.1 聚类效果图的对比 13

4.1.1 运行环境 13

4.1.2 聚类效果 13

4.2 各项性能参数对比 18

5. 总结与展望 20

5.1 总结 20

5.2 研究展望 20

5.2.1 截断距离的优化 20

5.2.2 聚类中心的自动化选择 21

5.2.3 聚类性能的提升 21

5.2.4 与其他机器学习方法的交叉配合 21

参考文献 21

致谢 23

基于密度的聚类算法分析与实现

罗波

，China

Abstract：In this paper, a novel clustering algorithm based on computational density peaks and rapid selection of cluster centers (CFSFDP) is studied. The essential idea of this algorithm is how to determine the clustering center quickly and efficiently. That is, only the data points that meet both of the following characteristics can be used as the clustering center. Compared with the surrounding elements that are surrounded by themselves, the local density value is larger than the neighboring elements. Neighbors; Relative distances from other denser elements. In this paper, the principle of the algorithm is firstly explained and analyzed. Then the pseudo-code of the algorithm is given, and a method of optimizing the cut-off distance through information entropy is proposed. Through comparison experiments, the CFSFDP algorithm, K-means algorithm, and DBSCAN algorithm are compared for the clustering effect. The data set used is the UCI data set. The results show that the CFSFDP algorithm can not only determine the clustering center well, but also has good performance in accuracy and running time. The limitation of this algorithm is that the processing of high latitude and large data is not good enough. In general, the CFSFDP algorithm can effectively identify cluster centers, and has good clustering effect on datasets with low-dimension and shape-distribution.

Key words：Clustering; density peak; clustering center; information entropy

1. 引言

选题背景及意义

近几十年来，随着计算机科学技术的蓬勃发展，人们在数据的获取与采集能力上不断进步，对数据的看法在不断改变，能否在大量数据里面找到有价值的内容成为研究的重点。随着信息处理技术和互联网技术的迅猛发展，有海量的数据和信息被我们收集，但是由于缺少有力的分析工具，且这些海量的数据和信息超过了人类的理解概括能力，所以研究有效的数据分析工具变得十分重要。聚类分析是一个古老且朴素的问题，人类在认识这个世界的过程中，通过区别事物及其构造之间的差别，才能认识事物之间的相似性。

聚类分析，即在数据中定位其所属的类别，在机器学习，统计学，数据挖掘和模式识别中是值得研究的问题。这有许多实际应用，例如：

商业和市场营销：在市场研究中，通过聚类将顾客群划分为具有类似购买习惯的群体以推断它们之间的关系，评估战略机会并确定竞争威胁；在营销和广告方面，通过聚类推荐系统需要一组类似的产品和客户，允许有针对性的营销策略，向类似的客户推荐类似的项目。

安全问题：通过聚类学习具有类似行为的个人组，例如支出模式，可以检测网络入侵和潜在的恶意行为。

生物学和医学：在医学成像中，通过聚类识别不同组织类型的区域用于发现不同的肿瘤并评估治疗效果。

现在聚类的方法结合机器学习等其他方法已经深入我们生活的方方面面，其价值不言而喻。现在，主流的聚类方法主要包括以下5类：

• • 1. 基于分层的聚类

对于聚类的一些应用，由层次聚类所定位的嵌套结构是直观的并且自然的。例如，在生物应用中，集群生物到物种和亚种。这些集群层次结构的位置可以采用两种不同的方法，即合并型（Bottom up）和分裂型（top down）两种方案。分裂型的方法开始与对单个整体簇的观察，并依次将其划分为更小的簇。相比之下，合并型的算法初始时将每一个数据点都组成一个单独的簇，通过算法不断的迭代，把那些互相邻近的簇兼并到一个新的簇，直到全部的元素形成一个簇或者满足某个设定的条件为止。

一个完整的层次聚类可能在计算上是昂贵的，并且对于大型数据集而言，在层次结构的每个级别处的所有聚类之间的距离的存储可能是不可行的^[13]。诸如减少平衡迭代和使用层次结构聚类的算法（BIRCH），旨在解决高内存使用率的问题。BIRCH通过仅存储聚类的摘要信息而不是原始观察来减少定位完整分层结构所需的内存。

• • 1. 基于划分的聚类

划分聚类的方法旨在将所有数据记录定位在一个单一的层次上。给定包含M个点的数据集，这种划分的聚类方法将会把数据划分为P个组，每个分组代表一个类别标签，而且每个类别分组至少蕴含一个数据点，每个数据点仅有一个类别标签。对于事先提供的P值，算法先计算出一个随机初始的分组情况，然后通过反复迭代计算来调整数据点的类别标签。聚类的准则在于同一簇中的点越近越好，不同簇中的点越远越好。通过这样的准则来使每一次迭代改进之后的分组方案都比前一次要好一点，最终算法会收敛于某个阈值，得到聚类结果。

这种方法往往比层次聚类在计算上花费更少，并且可能更适合数据集群的层次嵌套结构不直观的应用程序领域。例如，在一些医疗应用中，聚类任务可能是识别患有或不患有疾病的患者，因此分为两个截然不同的类别。使用这个本质想法的代表算法是k-means算法^[6]。

K-means算法存在一些问题，例如：如果数据集越大，会像贪心算法那样，陷入局部最小的可能性越大；要聚成多少个类别的K值需要预先设定，一开始选取的 K个点对聚类结果的影响很大；很难处理离群点和噪音点；只用于数值型数据。但是经过多年的研究，针对这些问题，已经有了不少解决对策^[7]，例如：对初始K值的设定很敏感，于是研究出了K-means ；提出了K-medoids来解决对噪音点敏感的问题；K-means对连续型数据效果好，而对于离散型数据集，效果很差，所以使用K-modes来扩展其功能；Kernel K-means通过引入核函数来解决非凸数据向高维空间的映射，从而完成聚类。

• • 1. 基于密度的聚类

在面对不规则形状分布的数据集时，K-means表现乏力，于是科学家们研究出了基于密度的聚类方法来系统解决这个问题，该算法同时也能有效的处理噪音点和离群点。其核心思想在于“画圈”，只要周围的点是密度可达的话，即能被“圈”到，就将其归为一类，通过不断寻找最大集合从而完成聚类。DBSCAN^[9]就是其中的经典代表，但其也存在一些不足：半径参数以及密度参数对聚类的结果有很大的影响；DBSCAN的参数是人为设置的，当待聚类的数据集密度稀疏程度不同时，由参数决定的判定标准可能会破坏原本数据集类别的自然结构，即不同的密度区域的聚类效果有很大差别，密度较小的可能会错误的划分为很多不同的类；同时DBSCAN对高维数据的处理速度不是很快，这点在近几年被发现^[8]。针对于DBSCAN对数据密集程度不一致的分布类型数据处理效果不是很好，而且需要人为的调整两个参数的问题，提出了OPTICS算法^[14]来解决。

DBSCAN算法作为传统的密度聚类算法，得到了广泛的应用。2015年的SIGMOD会议将最佳论文颁给了陶宇飞和其学生合作的文章《DBSCAN Revisited》^[8]。这篇文章有意思的地方是证明了著名的DBSCAN原始论文^[9]存在错误，后者中的一个算法时间复杂度实际上是基于错误的分析。在2014年，在KDD会议上，将经受时间检验奖（test of time award）颁给了DBSCAN 的原始论文，这篇论文到现在有8000多的引用量，但是从论文发表到现在的17年时间里，居然没有一个人找出其中存在的错误。不过，由于其较好的聚类效果以及简单的思想，还是成为主流密度聚类算法，并且在一些领域中有很好的表现。

• • 1. 基于网格的聚类

基于网格的聚类方法的思想是：先将待聚类的数据空间分割为相同的单元，数据点就有可能掉落在这些单元中，此时这种聚类方法只关注单个单元里面的数据点，统计其相关信息，例如最大值、最小值以及平均值。然后通过迭代和递归的方法对空间进行再划分。这些统计出来的数据会储存起来，可以作为聚类的标准，也可以用于对其他机器学习方法的前期准备工作^[15]。代表算法有：STING，CLIQUE等。基于网格的聚类方法只计算单元内的数据信息，因此该算法的优点在于计算速度很快，其速度与数据对象的个数无关。但是基于网格的聚类也存在一些问题：参数太多而且很敏感、不规则分布的数据集无法进行有效的处理、当维数增加时计算速度太慢等。

• • 1. 其他聚类方法

基于模型的聚类（model-based clustering）算法思想是：对每一个待观测集合都设定了有限个模型，即数据集是由有限个模型生成的。这个混合模型的每一个组件都代表了一个聚类。将每一个观测值分配给具有产生他们的最高概率的混合成分（即聚类），从而完成对数据集的分类。尽管组成一个数据集的概率分布可以有很多种方式，但是我们在实践中一般采用设定高斯混合模型（GMM）^[12]。在这种情况下，可以通过使用期望最大化（EM）算法的最大似然估计来完成模型参数的估计。这种方法使用缺失聚类标签的形式来扩张缺失的数据，并且在给定目前对混合模型中参数的估计值的情况下获取聚类标签的期望值之间进行迭代，然后在给定估计值的情况下最大化参数的可能聚类情况。这个迭代过程一直到收敛，最后返回估计参数以及聚类的分配向量。

剩余内容已隐藏，请支付后下载全文，论文总字数：19770字

相关图片展示：