论文总字数:12681字
目 录
1 绪论 5
1.1研究目的及意义 5
1.2蚁群算法的产生 5
1.3蚁群算法的研究现状 5
1.3问题的提出 6
2 蚁群算法简介 7
2.1基本蚁群算法 7
2.1.1 蚁群算法的仿生学原理 7
2.1.2人工蚂蚁的概念 8
2.2 蚁群算法的基本模型 8
2.2.1 蚁群初始化 8
2.2.2信息素的更新 8
2.2.3蚁群算法模型的建立 9
2.3 蚁群算法的基本流程 10
2.3.1基本蚁群算法的步骤 10
2.3.2控制参数的选择 11
3 算例分析 11
3.1蚁群算法用于测量数据处理中的非线性模型参数估计 11
3.2蚁群算法用于测量平面控制网优化设计中的TSP问题 13
4 结束语 15
4.1总结与结论 15
4.2展望 16
参考文献 16
致谢 17
蚁群算法在测量数据处理中的应用研究
储世杨
, China
Abstract: Ant colony algorithm is the process of searching for food through the simulation of ant colony, which can achieve the goal of solving the difficult combination directly. Through simulation of ant foraging in walking, the ants in the process of walking will leave pheromone, and ants in the shorter path will release more pheromone, stay in the shortest path above the ants will more and more, so that the ants in the shortest path of the above information hormone concentration highest, and the final, find the global optimal solution. Are briefly introduced in this paper the basic principle of ant colony algorithm and its application in the treatment of the nonlinear problem in measurement data processing, with other algorithm, and we compared the calculation results show that the solution accuracy of the ant colony algorithm is higher and is not easy to fall into local optimal solution.
Keywords: ant colony algorithm; measurement data processing; parameter estimation
1 绪论
1.1研究目的及意义
如今,科学与技术的发展正朝着一个多元化方向进行,于此同时,科学家们也对科技发展提出了更高新的展望,关于优化算法的研究也随着科学技术的快速发展而得到了很大的重视。优化技术是当今数学界用于数据处理的一种重要手段,尤其在用于求解复杂优化问题中效果非常显著,近期以来一直广受人们的重视,而目前优化算法已经成为了很多科学研究的重要手段。为了解决复杂的非线性问题,各种智能算法被提出来,应用范围也遍及各个领域,本文的目的就是为了求解测绘领域中一些非线性问题,并分析蚁群算法在测绘数据处理中的优势和劣势,以此分析该算法在测绘领域的有效性。
1.2蚁群算法的产生
上世纪五十年代中期,仿生学渐渐成熟。在生物进化论的启发下,一套较为完善的算法被人们挖掘出来,能够处理很多较为复杂的优化问题,随着时间的推移并一步一步走向成熟。而蚁群算法(Ant Colony System, AS)是上世纪九十年代由M.Dorigo等首先提出来的一种模拟生物的优化算法。自从蚁群算法被提出以来,许多相关算法的框架被提出来。1998年,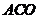 的第一届学术会议
的第一届学术会议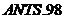 召开, 更引起了研究者的广泛关注。
召开, 更引起了研究者的广泛关注。
1.3蚁群算法的研究现状
蚁群算法(ant colony optimization, ACO),是机率型算法,它可以在图中找出优化的路径。作为模拟进化算法,我们通过研究发现蚁群算法有很多其他算法不具有的优秀方面。我们设置一个有关于优化PID控制器参数的问题,把遗传算法设计的结果和蚁群算法设计的结果相对比。得出的结论显示,蚁群算法作为一种新的模拟进化优化方法,应用价值方面和有效性方面都很好。
蚁群算法属于群智理论。群智理论可以分为两种:蚁群算法与微粒群算法。蚁群算法其实就是对蚂蚁群寻找食物的模仿,已在许多离散优化问题成功应用。微粒群算法同样是对一些比较单纯的容易的社会系统的模仿,一开始就是模仿鸟群寻找食物,但是后来人们觉得它是很棒的优化工具。和平常一些根据梯度的应用优化算法有所不一样,概率搜索算法是群智能算法的关键。尽管概率搜索算法一般情况要使用相当多的评价函数,但是和传统的演化算法以及梯度方法比较而言,它的长处还是很突出的 ,主要的表现有以下几个方面:
1)没有集中控制约束,个别和个体出现问题不会殃及整个问题的解答,使得系统有很好的可靠性;
2)用间接交流信息的方法,保证了整个系统的延展性;
3)使用并列行的分布式算法,让多处理器得到充足的使用;
4)不会限制问题是否有连续性;
5)算法可以简单实现。
群智能方法容易达成,算法只有一些基础的数学行为,而且CPU和内存都不用很高都能完成这些数据处理。并且群智能方法仅仅只要目标函数的结果值,不需要它的梯度信息。通过应用方法研究以及得出结果的群智能理论说明群智能方法是一种新的并且可以高效的解决问题的全局优化方面的方法。更加重要是,群智能的分布式特点以及内在的并行性为解决许多的用数据库的模式存在的数据供给了技术支持。不管是从应用研究的方面分析来看,还是从理论研究的方面分析来看,群智能理论和其研究发展都有很重要的现实价值与学术意义。
1992年,意大利的Marco Dorigo等人[1]提出了蚁群算法,并把蚁群算法首先运用在处理TSP(Traveling Salesman Problem)问题上。通过实验的结果来阐述蚁群算法很稳定以及寻找较优解的能力强,同时也存在自身的不足之处,在收敛速度方面可能有点迟缓、计算时发生停滞等。蚁群算法的提出引起了国内外学者和专家的强烈关注,同时关于蚁群算法的不足之处,提出了非常多的得到改进的蚁群算法。L. M. Gambardella和M.Dorigo[2]在前人的基础上又提出了Ant-Q算法,Ant-Q算法通过伪随机比例的状态转移规则代替蚁群算法的随机比例转移规则。这样使得Ant-Q算法构建解的过程可靠性得到了提高。除此之外,Ant-Q算法还采用部分信息素更新机制以及全局的信息素更新中得到最优解。M.Dorigo等人[3]还在Ant-Q算法的基础上提出蚁群系统(Ant Colony System,简称ACS ) ,蚁群系统算法是Ant-Q算法的一种特殊案例,运行起来更加容易,并且在解决TSP问题时显得游刃有余。Stutzle与Hoss[4] ,推出了最大-最小的蚂蚁系统(MAX-MIN Ant System,简称MMAS),这个算法的最大的特点在于设置了信息素的上下限能够有效地避免计算过程中过早发生停滞的现象。Bullnheimer等人[5]提出了基于排序的蚂蚁系统(Rank-based Version of Ant System,简称ASranx),这种算法在计算过程中每做完一次的迭代之后。都会把蚂蚁经过路线的长度按顺序进行排列,并将不同的权重分配给对应长度的路线,路线长度较短的权重大一点。由于蚂蚁系统存在检索速度比较慢以及质量不好的缺陷,Cordon[6]又提出了最优——最差蚂蚁的系统(Best-Worst Ant System,简称BWAS)。这个算法的核心是把理论上的最优解进一步的优化,从而使得最差解减弱,这样就会使得最优路径和最差路径上信息素的量差距变得越来越大。
国内关于蚁群算法的研究开展于九十年代末,现在中国的学者对蚁群算法的主要研究是对算法的应用方面与改进方面。吴庆洪与张纪会等人[7]将变异机制导入基本蚁群算法中,推出拥有变异特性的蚁群算法,使得算法变得简洁明了。吴斌与史忠植[8]率先将相遇算法引入到蚁群算法中,有效地提升了蚂蚁每次周游的速度和效果。谢剑英与王颖[9]将自适应的变化算法的挥发度等一些系数引入蚁群算法中,推出了一种自适应的蚁群算法,在解决一些局部最小而全局未必最优的问题中取得较好的结果。覃刚力与杨家本[10]提出了一种能够自己调节信息素的蚁群算法,并通过人工蚂蚁的求解的过程,来分配道路上的信息素。
1.3问题的提出
在现代测绘工作中,经常会遇到处理非线性模型的问题。随着科技的不断进步,在处理非线性问题上的精度要求也越来越高了。由于线性化近似处理的方法所带来的模型误差往往较大,不能够满足要求。
近年来,国内外的学者另辟蹊径,提出了许多人工智能算法,并且下迅速得到了应用,其主要优点在于求解精度高、并发性以及较强的鲁棒性。除了已经得到公认的遗传算法、模拟退火法、粒子群算法等,蚁群算法也逐渐开始被人们所认知。由于蚁群算法具有很强的搜索能力;分布式计算能够解决个体冗余而出过早收敛的问题,本文将蚁群算法引入到测量数据的处理中,将蚁群算法应用于非线性模型的参数估计,以得到高精度的参数估值。
2 蚁群算法简介
2.1基本蚁群算法
2.1.1 蚁群算法的仿生学原理
蚂蚁在觅食的过程中,能够在没有外界提示下发现蚁窝到食物源的最短途径,尽管在开始时不同的蚂蚁会选择不同的路径,但最终,所有的蚂蚁聚集在最短路径上。蚂蚁在寻找最短路径的过程中有一种正反馈的调节机制,蚂蚁会在经过的路径分泌一定量的信息素,而且能够感知这种信息素强度并朝这种信息素强度高的方向聚集。聚集过来的蚂蚁又会在该条路径下面留下信息素,随着蚂蚁数量的不断增加信息素的浓度也会不断的增加,形成一种正反馈的调节机制。最终通过最短路径上的蚂蚁最多,所以留在最短路径上面的蚂蚁的数量就最多。蚁群就是通过这种信息素来不断地反馈信息来调节行走的路线,来找到一条从蚁窝到食物源的最佳路径。
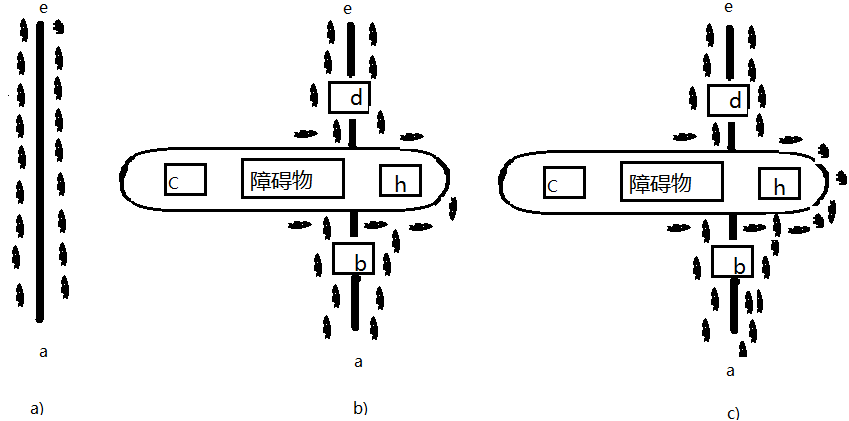
图1 蚁群模拟图[11]
如图1所示,在没有障碍物的情况下所有蚂蚁在a)的路径下由a到达e,当放入障碍物时如图b)部分蚂蚁会由a点经过b、c、d到达e点称为路线1,另一部分蚂蚁会由a点经过b、h、d到达e点成为路线2,但是随时间的推移,由于路线2的距离比路线1更短,留在路线2上面的信息素的含量闭合路线1要高,所以逐渐的蚂蚁都会选择行走路线2,最终,如图c)所有蚂蚁都会选择行走路线2。
2.1.2人工蚂蚁的概念
蚁群算法中的蚂蚁只是根据现实蚂蚁觅食行为抽象出来的一种人工蚂蚁。这种人工蚂蚁其实和现实蚂蚁相同,都是依靠蚂蚁所分泌的一种信息素为介质从而进行信息的交流。通过一种互相协作的模式来配合完成寻找最短路径的共同任务。如果完全按照现实中的蚂蚁这种正反馈的调节机制来进行的话,可能在真正的解决实际的优化问题的时候计算的时间可能很长,可以比拟成一个数量相当庞大的蚁群和存在很多障碍物的路径,这就使得计算的量相当的庞大,并且还有可能会出现局部收敛的情况即局部取得最优解而全局未必最优。人工蚂蚁与现实蚂蚁的异同:人工蚂蚁是具有一定记忆能力,它可以记住已经走过的所有路径,这样就能够保证不会再走重复的路径。但是现实的蚁群不具有记忆能力,是通过信息素的提示来区别已经走过的路径和未行走的路径。
2.2 蚁群算法的基本模型
2.2.1 蚁群初始化
在 个相互连通的点中,要解决要找出一条连接所有点的最短的闭合回路的问题。假设
个相互连通的点中,要解决要找出一条连接所有点的最短的闭合回路的问题。假设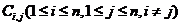 表示从第
表示从第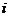 个点到第
个点到第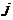 个点的距离,也可以代表
个点的距离,也可以代表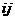 边上的权。把
边上的权。把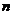 个点,每2个点相连接;抽象出由
个点,每2个点相连接;抽象出由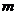 只蚂蚁构成的蚁群;每只蚂蚁任选一个点作为起点;初始时刻留在每条边上的信息素的浓度设为
只蚂蚁构成的蚁群;每只蚂蚁任选一个点作为起点;初始时刻留在每条边上的信息素的浓度设为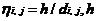 为常数,
为常数,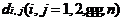 为
为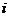 点到
点到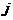 点的距离;设t时刻,留在
点的距离;设t时刻,留在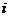 点的蚂蚁得数量为
点的蚂蚁得数量为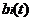 ,留在
,留在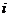
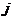 边上的信息素浓度为
边上的信息素浓度为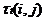 。于是有
。于是有
剩余内容已隐藏,请支付后下载全文,论文总字数:12681字
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


