论文总字数：12721字

目 录

1 绪论 4

1.1 课题背景及研究目的与意义 4

1.1.1 研究背景 4

1.1.2 研究目的和意义 4

1.2 混合蛙跳算法的国内外研究现状 4

1.3 问题的提出 5

1.4本文研究内容 5

2 混合蛙跳算法简介 6

2.1 SFLA算法基本思想 6

2.1.1 SFLA算法的仿生学原理 6

2.1.2 SFLA算法的数学模型 6

2.1.3 算法的参数设置 7

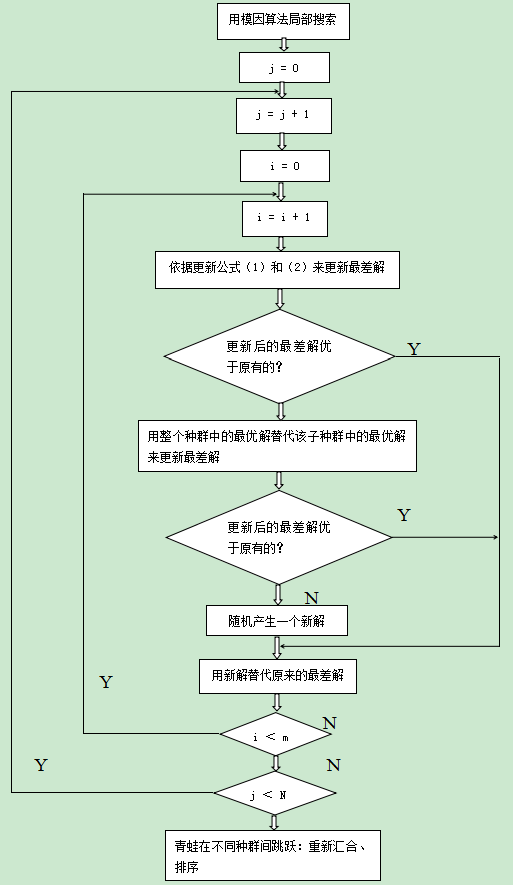
2.2 SFLA算法基本流程 7

3 算例分析与应用 10

3.1 算例介绍 10

3.2 结果分析 10

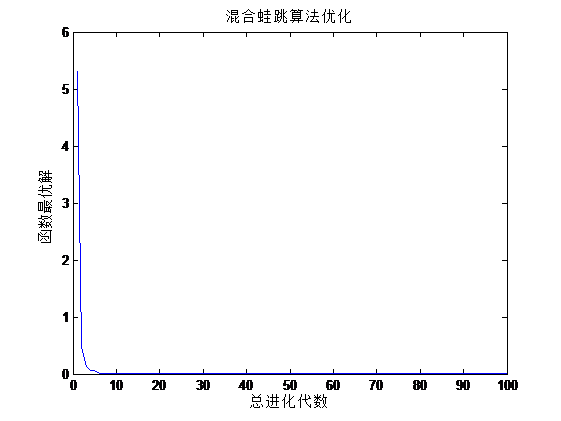
3.2.1 测试结果 10

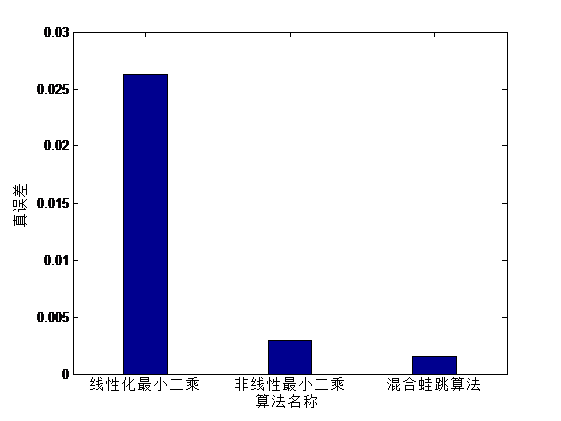
3.2.2 与其他算法对比分析 11

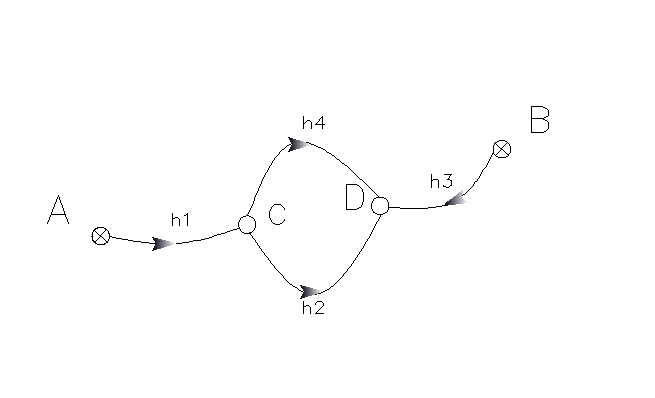
3.3.1 构建平差模型 13

3.3.2 算法应用于平差的结果 14

4 结论与展望 15

4.1 总结与结论 15

4.2 展望 15

参考文献 17

致谢 18

混合蛙跳算法在水准网平差中的应用研究

孙渡

, China

Abstract：Parameter estimation of nonlinear system is an important part of modern control field, and it is also an important part of surveying adjustment in surveying and mapping major.Traditional nonlinear parameter estimation algorithm has strong constraints on the estimation model, low computational accuracy, slow search speed, and easy to fall into local optimum..MATLAB is used to invoke the shuffled frog leaping algorithm, iterative calculation of objective function examples, the results of parameter estimation is (5.422743, -0.255669), The accuracy is much higher than that of the linear least square method.The results show that the shuffled frog leaping algorithm is an effective method to estimate the nonlinear model parameters. Finally, the hybrid frog leaping algorithm is applied to a specific wire network adjustment computation examples to verify the algorithm in the level network adjustment in study of feasibility and superiority.

Key words：shuffled frog leaping algorithm;nonlinear model;parameter estimation;swarm intelligence;adjustment of level network

1 绪论

1.1 课题背景及研究目的与意义

1.1.1 研究背景

当前，在测绘领域中，我们经常会遇到非线性方程组的求解问题，内业处理时往往面临大量的该类问题。所以，现在有很多学者致力于非线性方程问题的求解算法研究。到目前为止，解算非线性问题已经取得了令人瞩目的成就。运用传统求解算法如拟牛顿法、最速下降法以及信赖域法等求解精度较高、速度较快，但是对初始值的选取限制条件较多，当初始值不符合这些算法的要求时，就要另辟蹊径了。这时候，以粒子群算法、蚁群算法以及鱼群算法等为代表的群智能优化应运而生。这类算法对初始值的要求不高，但是缺点也很明显：易陷入局部最优，求解精度不高。

现代信息技术日新月异，实际生活中遇到的优化问题越来越复杂，许多问题呈现出多极

值、多目标、多维、不可微等特点，高效的智能优化技术的市场需求非常大。2003年，美

国学者Eusuff和Lansey将青蛙的觅食活动与优化问题联系在一起，提出一种新的群体智能

优化算法——混合蛙跳算法（SFLA）。混合蛙跳算法是一种亚启发式协同搜索算法，它把模因算法（MA）的模因进化和粒子群优化算法（PSO）的局部搜索思路两大优点融合进来，该算法参数较少、求解效率高、全局搜索能力强且易于实现^[12]。这些年来研究人员不断完善该算法，并将其广泛应用到工程中：如聚类分析、输电网规划设计、旅行商问题和背包问题等，这进一步说明了它在处理优化问题上的优势。混合蛙跳算法是智能优化领域新兴的一种智能优化算法，已逐渐成为相关领域的研究热点。

1.1.2 研究目的和意义

非线性模型参数估计是现代控制理论研究的一个重要研究方向，同时也是测量数据处理中的重要内容。传统的非线性参数估计算法对估计模型有较强的约束条件、计算精度较低、搜索速度慢、易陷入局部最优。混合蛙跳算法提出的时间较晚，在处理实际生活中的优化问题方面应用前景值得期待。很多群智能算法在非线性参数估计中已有上佳的表现，而混合蛙跳算法在这方面的应用不多。因此，研究混合蛙跳算法在非线性模型参数估计中的应用具有一定的现实意义。

1.2 混合蛙跳算法的国内外研究现状

混合蛙跳算法由Eusuff等人于2003年在文献[1]中第一次提出，提出伊始就受到国内外学者的高度重视，如今该算法已经成功应用到很多方面，成为研究人员们热衷的研究方向。目前该算法的研究成果并不是很多，研究内容也主要集中于对算法的改进以及实际应用。

2005年，Elbeltagi等将遗传算法、蚁群算法和粒子群算法三种方法综合对比，得出混合蛙跳算法在解决优化问题时的搜索速度最快^[2]的结论。2006年，Eusuff等从收敛速度方面与遗传算法进行对比，发现在解决组合优化问题时混合蛙跳算法卓有成效^[1]。这几年，众多研究人员针对混合蛙跳算法的缺点做出更新策略，得到了更加实用的蛙跳算法。文献[3]在经典混合蛙跳算法中引入加速搜索范围这一参数，将其用来研究连续和离散这两类问题，并通过具体的实验分析凸显出新参数起到的重要作用。文献[7]在创造性地混合蛙跳算法中引入了生物学的吸引排斥思想，不仅维持了种群的多样性，而且大大提高了算法的收敛速度，很好地解决了混合蛙跳算法在局部搜索时出现的“早熟收敛”。在处理背包问题时，文献[8]首倡基于0-1规划的数学模型，针对离散搜索空间对混合蛙跳算法进行改进，将改进的算法成功解决了背包问题。文献[9]提出了基于阈值选择策略的改进混合蛙跳算法，在局部更新的时候，青蛙个体的最大移动步长是随机的，跳跃也是随机的前后变化非常大，这种改进的混合蛙跳算法以减少个体的空间差异，来提高算法的性能。文献[11]建立了Markov链数学分析模型，分析了Markov链的性质，证明了青蛙族群状态序列是齐次Markov链。文献[13]对局部搜索的过程重新调整，在青蛙群体进行信息交换时采用变异思想，并用改进算法解决旅行商问题。

因为混合蛙跳算法提出的初衷就是为了解决水资源优化分配的，所以当前的研究方向基本上是将混合蛙跳算法与实际生活中的优化问题结合，并提出解决方案。值得注意的是，混合蛙跳算法的研究时间不长，没有完整的理论支撑，使得算法本身在逻辑上显得不是那么完美，所以目前的研究工作都还处于较低层次。尽管混合蛙跳算法优点明显，但它也存在寻优结果精度低以及计算速度慢等缺点，影响算法的性能。所以，当前工作的主要方向应该是完善混合蛙跳算法的理论基础，并对该算法的应用进行更深层次的探索。前者是解决算法自身的问题，提高算法性能，未解决复杂的非线性问题指引一条康庄大道；后者则会推动智能优化算法的发展，从而创造出巨大的社会价值。

1.3 问题的提出

在现代高精度的测量工作中，对非线性模型的参数估计一直是数据处理方面的难点与热点。用线性化近似处理的传统方式越来越不能满足测量数据处理的精度要求，最小二乘法和遗传算法、粒子群算法等经典的群智能算法应运而生，并取得了非常不错的成绩。但是，这些优化算法都或多或少有着较明显的缺陷，如最小二乘法对模型的约束条件有较高的要求；遗传算法计算量大，搜索速度较慢，在估计精度方面也有待进一步提高；粒子群算法对参数设置的限制条件较多，易陷入局部最优。

混合蛙跳算法是新兴的群智能优化算法之一，它参数少、计算速度较快、全局寻优能力强。本文主要针对测量数据处理面临的寻优精度不高、搜索速度较慢以及参数设置较多三个问题，将混合蛙跳算法运用到非线性模型参数估计中，用matlab对算例进行处理。因为混合蛙跳算法的局部搜索过程是参考的粒子群算法，所以可以预见的是，混合蛙跳算法在估计精度和搜索速度方面会与粒子群算法相近，与最小二乘法相比会有较大的提高。同时，与粒子群算法相比，混合蛙跳算法比较不易陷入局部最优。这些内容在第三部分是重点，本文会将处理结果与上面提到的几种算法的结果（已有）进行对比分析，以期获得预期的结果。

1.4本文研究内容

本文首先对混合蛙跳算法的基本原理进行了简单介绍，在此基础上，将混合蛙跳算法应用于非线性系统参数估计，通过对算例计算结果的分析以及与传统非线性方法的结果比较，检验混合蛙跳算法的性能，然后将混合蛙跳算法运用到水准网平差中以验证其可行性和优越性。最后是对本文的总结和展望。

2 混合蛙跳算法简介

2.1 SFLA算法基本思想

2.1.1 SFLA算法的仿生学原理

混合蛙跳算法是由青蛙觅食的行为获得灵感而产生的，所以这里就以青蛙觅食作为例子描述该算法的原理。

每只青蛙以不同的荷叶作为媒介，通过不停地随机跳跃逐渐接近所需要的食物。这个过程中如果有些青蛙同时到达一片荷叶上，它们就会互相分享自己的信息，我们姑且称之为信息交换。把所有青蛙分成若干小群体，那么规定每个小群体都有自己的文化，其中的每只青蛙也都各自有独特的文化，这里的文化在实际问题中相当于问题的解。在小群体中，每只青蛙的文化不仅会影响着其它青蛙的文化，且自己也会随之改变。在局部搜索过程中，小群体内部进行迭代计算，小群体的文化不断进化，促进单个青蛙向着最优解靠近。这个过程迭代一定次数后，小群体之间像青蛙个体一样进行相互作用，达到目的后即停止交流。子群体的青蛙个体随子群体进化到规定的代数，各子群体进行思想交换实现混合运算。与其它算法最大的不同在于，混合蛙跳算法融入了局部深度搜索和协调全局信息交换的策略，从而跳出局部极值点并向着全局最优解运行，这也体现了算法的本质特征。

2.1.2 SFLA算法的数学模型

我们设有包含P只青蛙的群体，它们随机分布在空间内，规定第i只青蛙所在的位置就是我们所要的第i个解，且Xi=(xi1,xi2…xis)，s表示空间维度。在确定所要解决的问题之后，我们首先要计算其目标函数，求出所有解的函数值，按照从大到小的顺序排列。然后把问题均分成M个部分，每个部分有N个解。我们执行这样的操作来合理分配这些解：把第i个解放到第i个部分中，分配好前M个解后，把第M i个解放也到第i个部分中……按照这样的策略完全分配这P个解。

剩余内容已隐藏，请支付后下载全文，论文总字数：12721字

相关图片展示：