论文总字数：16609字

目 录

1 绪论 1

§1.1研究目的及意义 1

§1.2群智能算法研究现状 2

§1.2.1群智能算法简介 2

§1.2.2萤火虫算法的产生与发展 2

§1.3问题的提出 3

§1.4本文研究内容 4

2 萤火虫算法简介 4

§2.1萤火虫算法基本思想 4

§2.1.1萤火虫算法的仿生学原理 4

§2.1.2萤火虫算法的基本概念和思想 5

§2.2萤火虫算法基本流程 5

§2.2.1控制参数的选择 5

§2.2.2智能优化策略分析 6

§2.2.3萤火虫算法基本流程 7

3 测量平差算例应用及其结果分析 7

§3.1算例一 7

§3.1.1算例介绍 7

§3.1.2结果分析 8

§3.2算例二 11

§3.2.1算例介绍 11

§3.2.2结果分析 12

§3.3小结 13

4 结论与分析 13

§4.1总结与讨论 13

§4.2展望 14

参考文献： 14

致 谢 16

萤火虫算法在测量数据处理中的应用研究

马慧

，China

Abstract： The Firefly Algorithm (FA) is affected by the nature of the Firefly exchange of information through a fluorescence to hunt, warn and breed, which inspired this kind of crowd behavior has evolved. It is more parallel and current than others. First, it is introduced in the paper theoretical concepts of firefly Algorithm, then, getting definition of the process and modeling from the mathematical descriptions of firefly algorithm. Finally, realize the Parameter estimation of nonlinear model function simulation test and get results. At the same time, comparing test results of firefly algorithm and other algorithm in the accuracy of the optimization results of function respectively. In the process of comparison, according to the result of test, the parameter of firefly algorithm close to the true answer and its residual is small, that means the fitting degree of firefly algorithm is good. This experiment can shows that the firefly algorithm on the accuracy of the optimization results and fitting degree of Parameter estimation of nonlinear model function is superior to genetic algorithm. It shows that the feasibility and effectiveness of firefly algorithm in the continuous space optimization.

Key words： Nonlinear model; Firefly Algorithm; The bionic swarm intelligent optimization algorithm; Parameter estimation

1 绪论

随着现代测量工作的发展，非线性模型在测绘工作中的比重逐渐增大，这是测量人员在实际工作中需要面对的重要问题。当前测绘工作中，对测量精度的要求正在日益提升，传统的线性化最小二乘的平差方法已不能满足日益进步的测量工作的需求^[1]。为此，改进利用最小二乘估计解决非线性模型以及加强其在测量数据处理中的应用研究开始逐渐走入测绘界许多学者的视野 ^[1]。近几十年来，国内外学者在该领域提出了一个重要的研究理论，并成功将其引入测绘工作——群体智能与仿生算法的应用研究。

§1.1研究目的及意义

现代测绘工作中，大多数的观测方程为非线性方程，在面对此类问题时，传统的做法是将非线性方程线性化，即在进行平差计算时，首先将非线性方程按台劳公式展开，取展开式的一次项，舍去剩余项，将其转化为线性方程。由于线性化做法略去二次以上各项，其过程必然引起模型误差^[2]。迄今为止，测绘工作的观测精度较从前已有了显著提高，这导致了有些建模产生的误差甚至大于观测产生的误差 ^[2]。因此，在平差过程中采用线性近似的理论去处理具有拥有较高精度的观测结果，反而会使测量误差增大，这违背了测量平差的初衷。随着现代科学技术的不断发展，对平差精度的要求正在不断提高，在这种背景下，越来越多的仿生群智能算法开始备受关注，以其快速精准的优势成为解决非线性模型参数估计的新生力量。

课题所研究的萤火虫算法(Firefly Algorithm， 即FA)，是基于生物群智能的研究而衍生出的一种寻优算法。该算法通过模拟萤火虫觅食、择偶、交配、繁衍等习性，模拟其通过产生荧光吸引彼此移动的行为来寻找最优解^[3]。萤火虫算法与其他群智能算法类似：算法中由于拥有多条搜索路径而体现出很强的并行性。其次，该算法只需利用目标的取值信息和函数信息，具有很强的通用性和普适性。因此，该算法被广泛应用于模式辨别、自动搜索、网络选择等多个领域^[4]。萤火虫算法过程中不要求具有严格的模型，对于目标函数也没有严格的约束条件，和经典算法相比，在计算复杂度上则表现的更加出色。本文将针对萤火虫算法的原理、优势、以及其在测绘领域的应用前景进行探讨，在用Matlab实现该算法的基础上，对测量数据进行算例分析，最终得出最优解。

§1.2群智能算法研究现状

§1.2.1群智能算法简介

20世纪40年代，美国学者Mc Culloch和Pitts提出二值神经元模型，这一模型为后来的仿生学算法研究奠定了至关重要的基础。在之后的六十多年间，受达尔文“适者生存”的启发，智能选择、信息处理和优化控制等方面的新兴智能算法飞速兴起和发展，群智能算法作为一种新兴的优化选择技术，以其众多的优势成为越来越多研究者所关注的焦点^[4]。

近几十年来，国内外学者通过分解、研究、模仿群体生活的动物的社会行为特征，提出了一系列模拟生态系统中物种群体生活的智能优化算法，几类比较有代表性的群智能优化算法主要以下几种：遗传算法(Genetic Algorithm， GA)完全从大自然中学习，从遗传学的角度解释了自然选择和优胜劣汰的生存法则。蚁群优化算法(Ant Colony System， ACO)利用分工合作的蚁群体系，适用于路径优化选择^[5]。粒子群算法(Particle Swarm Optimization， PSO)模拟了鸟群、鱼群等群体的合作觅食行为^[6]。细菌觅食优化算法(Bacteria Foraging Optimization Algorithm，BFOA)模拟大肠杆菌之间的觅食行为所包含的特征^[20-24]。上述几种算法就是通过学习或模拟某些生物生存因素、生存技能或生存性质的特殊现象。因此此类算法又被统称为群智能优化算法(Swarm Tntelligent Optimization Algorithms)^[7]。

群智能算法源于对自然界生物进化过程中繁衍、觅食、交配等行为的模拟。搜索和优化过程即视为成进化、觅食、繁殖和交配的过程；用搜索空间中无体积的点模拟自然界中的个体群体；将待解决的目标函数度量成个体对环境的适应能力或影响力；将个体间的适者生存的过程比为寻优过程中较优解取代较差解的迭代过程^[8]。这类算法对目标函数的形态和阶数没有特定要求，通常适用于大规模的、不宜进行求导运算的复杂结构优化问题。相对于传统的优化算法，群智能优化算法拥有理论简单、易于实现、寻优效果更优等优点^[9]。

§1.2.2萤火虫算法的产生与发展

萤火虫算法的概念最早是由剑桥大学的Xin-She Yang教授于2009年提出的，后来的一年中，Xin-She Yang教授先后发表了《对于萤火虫算法的随机优化的研究报告》、《萤火虫算法的多模优化问题》等研究论文，为萤火虫算法的成功应用奠定了基础^[4]。

目前，国内外学者将萤火虫算法进一步推广，将其应用到许多领域：2010年11月，Theofanis Apostolopoulos和Aristidis Vlachos发表研究了应用萤火虫算法解决经济排放负荷调度问题； 2012年10月，Surafel Luleseged Tilahun和Hong Choon Ong提出萤火虫算法的优化问题^[10]。国内关于萤火虫算法的研究工作也相继展开，叶春明教授在2011年到2013年间先后发表论文介绍了萤火虫算法，以及提出了置换流水车间调度问题的萤火虫算法、应用萤火虫算法求解PFSP问题、Job-shop调度问题和置换流水线问题等^[11]。此外，国内主要研究还有：2011年7月，王迎菊和周永权提出了一种基于荧光素扩散的人工萤火虫算法；2012年3月，彭伟和汪镭提出了基于萤火虫算法的神经网络CPI预测模型；2012年8月，袁际军发表基于多目标萤火虫算法的可调节产品族优化设计；2013年3月，曾冰、李明富、张翼等人发表了基于萤火虫算法的装配序列规划研究；2013年4月，李铁、姚晔等人发表了基于改进型人工萤火虫算法的云计算资源^[10]。

我国对于萤火虫算法的研究从21世纪初开始，十几年间一直处于上升期。特别是近年来，萤火虫算法的应用在很多领域取得了显著成效。据不完全统计，目前有关萤火虫算法、进化算法的研究论文就多达600余篇。

§1.3问题的提出

在经典平差，即最小二乘平差中，具有最优性的条件是：1、函数模型为线性模型；2、观测误差为服从正态分布的偶然误差。而在现代测绘工作中，非线性模型的出现频率比线性模型更高，即：，若（模型误差），破坏了系统误差为零的假设，则导致：1、最小二乘解为有偏估计；2、最优性值得怀疑^[2]。

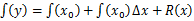
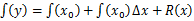
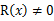
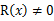
传统非线性最小二乘估计的解法如下：

剩余内容已隐藏，请支付后下载全文，论文总字数：16609字