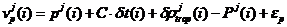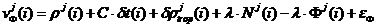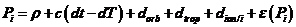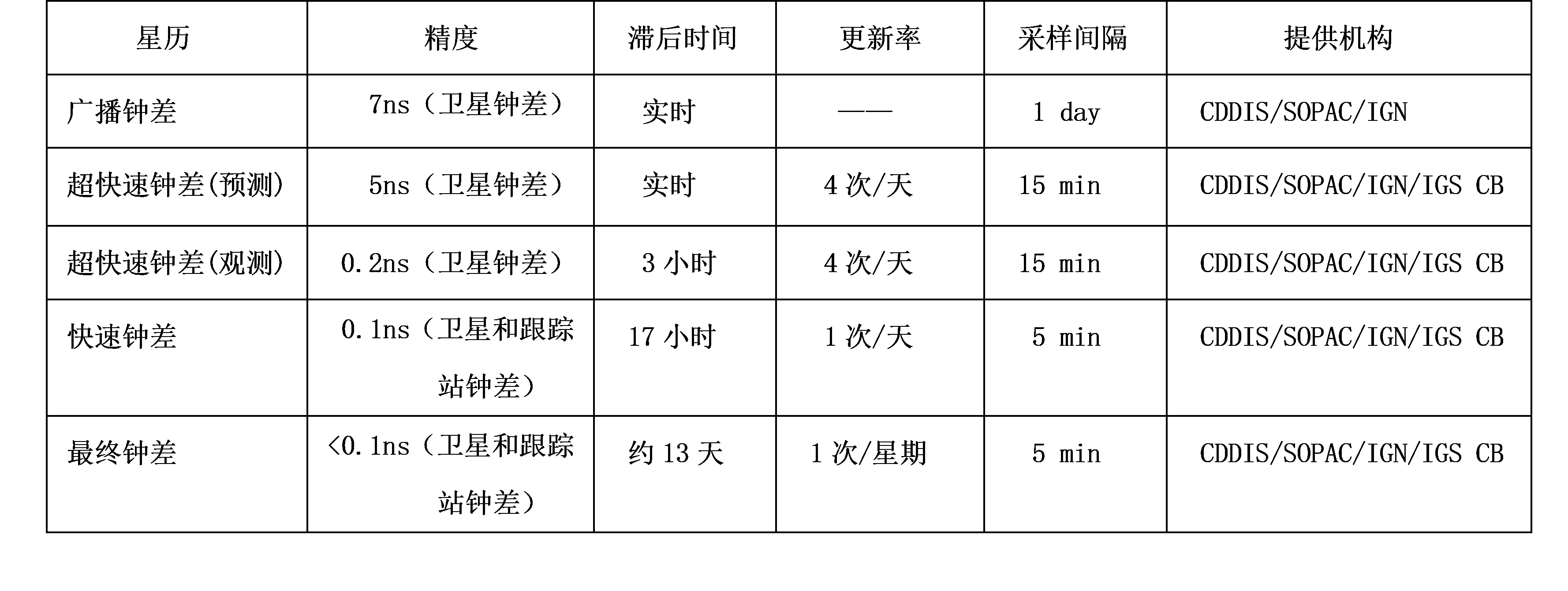论文总字数:14349字
目 录
1绪论 1
1.1研究背景及意义 1
1.2国内外研究现状 1
2 精密单点定位的原理与误差 2
2.1 精密单点定位的原理 2
2.2 PPP观测方程 2
2.3 PPP的观测误差源 3
2.3.1 星历误差和卫星时钟误差 3
2.3.2 对流层折射误差 3
2.3.3 电离层折射误差 4
3 精密单点定位数学模型与参数估计方法 4
3.1 PPP数学模型 4
3.1.1 传统模型 4
3.1.2 UofC模型 5
3.1.3 无模糊度模型 5
3.1.4 PPP的三种模型特点及区别 6
3.2卡尔曼滤波参数估计方法 6
4数据试验与成果分析 7
4.1数据获取 7
4.2 数据处理流程 9
4.3数据试验与成果分析 10
5 总结与展望 12
5.1 总结 12
5.2 展望 13
参考文献 13
致谢 15
GPS精密单点定位原理及其实践
尹卓
,China
ABSTRACT: This paper studies the Precise Point Positioning the basic theory, introduced the research status of Precise Point Positioning, analyzes the main error sources and their corresponding correction model to explain precise point positioning parameter estimation method - Kalman filtering parameters estimation methods, explored three positioning model for precise point positioning:the traditional model, UofC models with and without ambiguity model. Positioning the data of global IGS stations ,then we analyze the size of error and convergence time on the basis. In local Cartesian coordinates coordinate system,the positioning error is almost less than 2cm in the N-direction and 5cm in the E-direction,while the positioning error is larger than them in the U-direction.Although most of the error are in the interval [0,5],points are distributed more discretely.
Key words: Precise Point Positioning (PPP); Model ;Error Of Positioning ; International GPS Service(IGS)
1 绪论
1.1研究背景及意义
全球定位系统(Global Positioning System,GPS)自投入使用以来,在测量定位领域中得到了普遍的应用。在当前的GPS测量作业中 ,最为常见的大致包含标准单点定位和差分GPS定位。传统的单点定位虽然仅需单台GPS接收机便能够实时作业,且大范围应用于导航领域,但是精度不高,可能无法达到一些用户高精度定位的要求。而差分GPS定位(DGPS)技术尽管误差相对较小,却不能单基站定位。作业时不单要考虑到两者间的远近程度,其耗费成本也会随之增加[1]。
在GPS卫星定位快速发展的背景下,美国JPL(Jet Propulsion Laboratory)的Zumberger J F等学者于1997年提供了他们的解决方法,通过全球对单台GPS接收机所采集的相位观测值和双频测码伪距进行定位解算。使其能够在全世界区域内完成定位并得出精度为厘米级的结果。单台GPS接收机定位,极大地提升外业的工作效率以及仪器的利用程度。且它不需要依赖基准站,不会因距离远近而受到限制。在一定程度上,精密单点定位消除了标准单点定位与差分定位的劣势,综合了它们各自的优点。此外,它处理数据十分方便,不需要平差,测量点位数据之间无累积误差且精度均匀,因而该技术已成为国内外卫星大地测量研究领域的热门方向之一。
然而,精密单点定位在现阶段仍暴露出一些问题,主要体现在以下几个方面:
(1)定位的模型问题。PPP利用的函数模型,是影响其误差的重要原因。
(2)精确地施加各种必要的改正。由于PPP对精度的要求极高,因此需要精准地削弱乃至消除影响结果的误差。
(3)获取信号发出瞬间的卫星坐标和钟差。当前IGS上的卫星精密星历和钟差每5分钟或15分钟更新一次,使用Lagrange等插值法即可获取观测时刻卫星的空间位置。但卫星钟差变化不定,用插值方法处理会导致误差较大。
(4)参数的估计问题。PPP的观测量大,未知参数较多,如何使用恰当的函数模型和参数估计方法精准和快速地估计参数,成为PPP研究领域的重中之重。
1.2国内外研究现状
1997年,Zumbeger等人提出了精密单点定位方法,通过他们自己编制的GIPSY软件定位解算,使得单天解误差在水平方向上控制在1厘米以内,高程方向上控制在2厘米以内[2]。
Heroux 等人通过一段时间的静态定位解算,其成果显示误差也达到了厘米级[3]。加拿大卡尔加里大学的Gao等人对PPP的原理和算法进行了深度的剖析[4]。德国的GFZ和加拿大的GSD开发了PPP软件系统,得出了同等精度的静态和动态解算结果。美国的Han等学者展开了详尽的研究,依据估算得到的高精度卫星钟差和已知的卫星空间坐标解算出待测点的坐标。加拿大纽布伦斯威克大学的Leandro博士通过PPP技术演算出估算电离层延迟和卫星钟差的公式,极大地延伸了PPP的运用领域。
GPS精密单点定位虽然在国内的研究起步略迟,但是发展速度飞快。2002年武汉大学的叶世榕博士利用自己编制的软件定位解算,单天解的精度为在B、H、N方向分别小于1厘米、2厘米、3厘米[5]。随后武汉大学的张小红教授独立研发了PPP数据处理的商业化软件TriP,其解算精度与国外软件持平[6-7]。香港理工大学的陈武博士将PPP技术成功运用在海面变化的监测。韩保民等学者将PPP解算结果与双频差分定位得到的坐标对比,成功证实了定位误差能够保持在厘米级以内[8]。洪樱等人探究了高精度卫星星历和卫星钟的插值方法[9]。
2 精密单点定位的原理与误差
2.1 精密单点定位的原理
当下的GPS空间定位技术多数采用的是差分数学模型。差分定位作业要满足至少2台接收机工作并同步观测,该方法主要是通过差分去除两个测站共有的系统误差,以便能够实现精准的相对定位。
GPS定位过程中会存在着各类系统性误差,因而对它们建立起对应的函数模型,通过各自估计和改正已达到对它们的削弱和消除。将GPS后处理星历和卫星钟差,作为起算数据,用来计算未知点的空间位置。
在GPS精密单点定位技术中,利用精密星历所提供的卫星钟差,可消除观测方程中的卫星钟差项。采用双频观测值,建立电离层误差改正模型,可以消除电离层折射误差的影响。综上,精密单点定位的误差方程可表示为:
式中,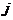 为卫星号,
为卫星号,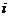 为相应的观测历元,
为相应的观测历元,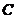 为真空中光的传播速度。
为真空中光的传播速度。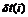 是接收机钟差,
是接收机钟差, 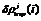 为对流层延迟影响。
为对流层延迟影响。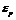 ,
,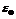 为多路径、观测噪声等未模型化的误差影响。
为多路径、观测噪声等未模型化的误差影响。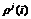 ,
,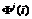 为相应卫星
为相应卫星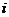 历元的观测值的线性组合。
历元的观测值的线性组合。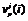 ,
,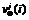 为该历元的观测值误差,
为该历元的观测值误差,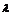 为载波的波长。
为载波的波长。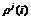 是卫星信号发射时刻的卫星的位置,与接收机接收信号的站星距离。
是卫星信号发射时刻的卫星的位置,与接收机接收信号的站星距离。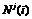 为整周未知数。
为整周未知数。
2.2 PPP观测方程
伪距的观测方程如式(2-3)所示,载波相位测量的观测方程如式(2-4)所示。在
剩余内容已隐藏,请支付后下载全文,论文总字数:14349字
相关图片展示:
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;