论文总字数：22285字

目 录

1.绪言 1

1.1研究意义 1

1.3研究内容和研究目标 1

1.2国内外研究现状及存在的问题 2

1.4研究区概况 2

2. Pearson（皮尔森）相关性分析 4

2.1原理 4

2.2进行Pearson相关分析的条件 5

3. 多源滑坡监测数据获取方法 7

3.1 多源数据的概念 7

3.2 GNSS表面位移监测 7

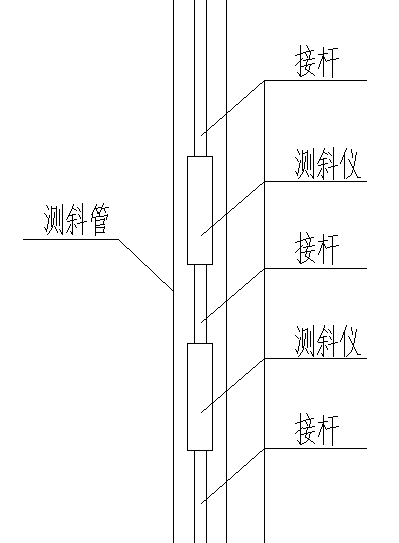
3.3 深部位移 9

3.4 土壤湿度 10

3.5 孔隙水压力和地下水位 10

3.7 滑坡数据预警平台 10

4.多源数据处理 12

4.1数据预处理 12

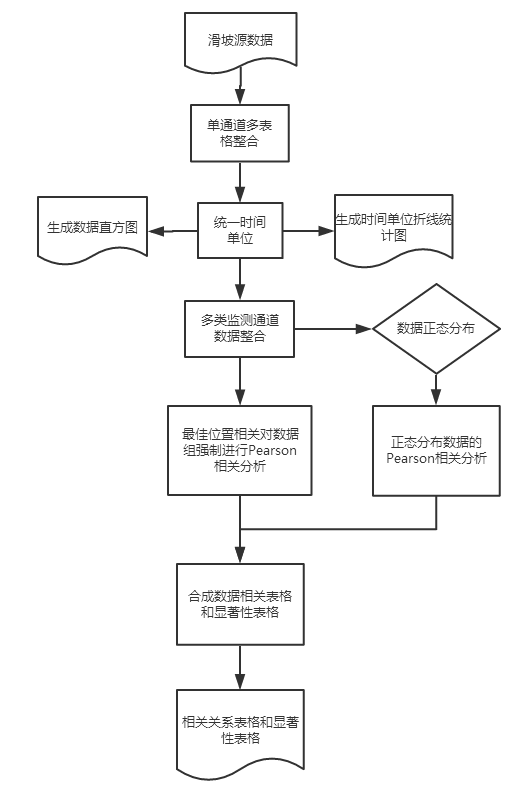
4.2数据处理 12

4.3 SPSS Pearson相关分析 14

4.4 MATLAB图绘制 14

5.数据成果与分析 15

5.1最进位置相关的数据相关分析 15

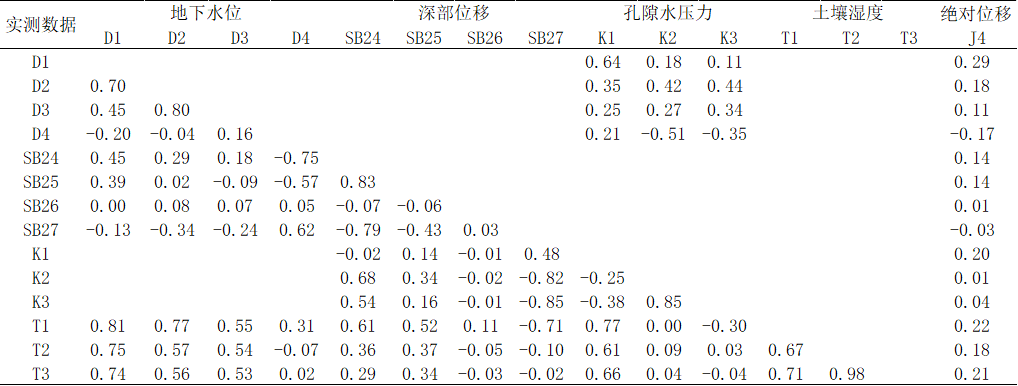
5.1.1相关系数矩阵分析 15

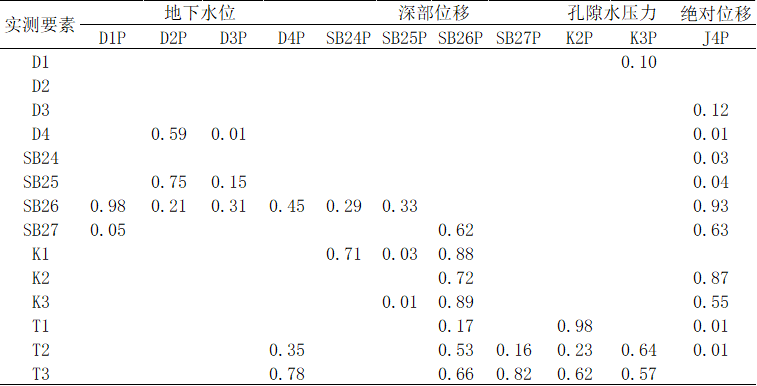
5.1.2显著性矩阵分析 16

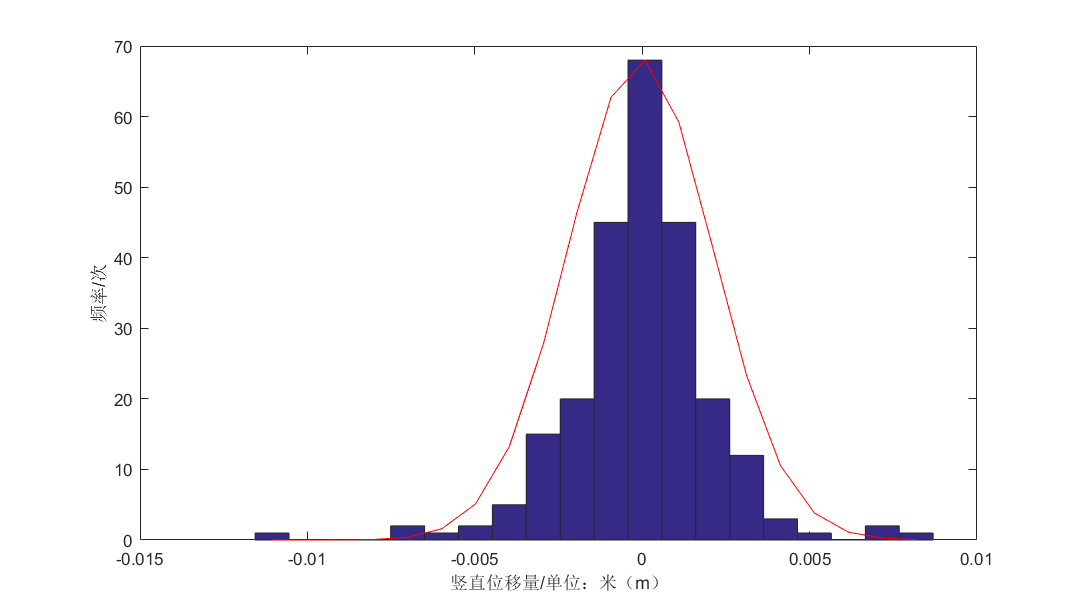
5.2数据正态分布时的数据相关分析 17

5.2.1相关系数矩阵分析 18

5.2.2正态分布数据相关性分析显著性分析 19

5.3滑坡位移时间和空间上的分析 20

5.3.1表面位移分析 20

5.3.2数据的时间分析 21

5.4结论 23

5.5不足与展望 23

参考文献： 24

致谢 26

多源滑坡实测数据关联性和时空特征分析

吴宇飞

Abstract: In order to solve the data validity of landslide system, the inherent correlation of multi-source measured data is studied and analyzed. This paper mainly studies the correlation between the data, explains the correlation between the landslides monitoring data sources and the analysis of the landslides data in time and space. Correlation is related to Pearson (Pearson), making scatter plots and bivariate correlation analysis using SPSS data analysis software. The results show that there is a strong correlation between the groundwater level, pore water pressure and soil moisture data (generally between 0.6~0.8), and the highest correlation between soil moisture and deep displacement is -0.75, the correlation of surface displacement and groundwater level is high in 0.4~0.5; it is also not found in each group of data. There are correlations, such as partial surface displacement and groundwater level. The results can be directly applied to the late maintenance of the monitoring system, and the monitoring points should be added and changed to make the data more practical in forecasting and forecasting.

Key words: Multisource data; data correlation; landslide monitoring; feature analysis.

1.绪言

1.1研究意义

滑坡是指在地下水活动、雨水入侵、地震活动和人工边坡开挖等因素的影响下，在一定的软弱面或软弱带上，斜坡上的岩土体的地质过程和自然现象^[1]。

近几年，随着社会的发展需求，很多的大工程落成，边坡的滑坡问题越来越受到重视，市场上不断出现新的滑坡监测系统。然而由于当前对滑坡实测数据的分析没有形成有效的分析和认知，导致实测数据在分析和使用时没有具备有效的理论资料支撑。

因此，本文的研究有一下几个方面的意义：

1. ‌对滑坡监测系统的建设有重要意义，其中监测系统传感器的选择和安装提供参考。根据实际生产发现，监测系统选用的传感器，安装的方法步骤，对监测效果以及数据的获取有很大的影响，而作为产物的数据，数据分析反应前者的有效性^[2，3，4]，因此数据相关性和时空特征分析对系统的建设有重要意义。
2. ‌对系统后期的升级换代，传感器监测点的选择提供参考。滑坡监测都属于长期持续的工作，设备难免都会有出现老化损坏的情况，同时设备的精度性能等需要根据实测数据的特征分析结果进行更改选择，提高传感器的有效性和可靠性^[5,6]，也为监测的智能化与自动化提供理论资料。
3. ‌另一方面，对研究滑坡影响因子、产生机理^[7，8]、诱发因子^[9]、滑坡相关数据临界值^[10]、以及实测数据的深度挖掘^[11]具有重要意义。随着滑坡监测的增加和行业技术成熟，对数据会进行更详细的研究，因此数据相关性和特征分析会提供可靠的资料和科学依据。

1.2研究内容和研究目标

合滑坡预警系统的滑坡数据进行相关性研究，并合理运用已有的论文资料和研究成果进行科学分析。

1. 根据已有资料及现场勘察综合判断测区滑坡的性质和状态。
2. 根据滑坡监测系统的历史数据进行初步分析判断滑坡变化的规律和趋势。
3. 利用相关性分析手段计算滑坡各项数据在各时间段内数据的关联度，根据数据的关联度的大小预测数据间的相关性，用显著性来衡量数据的可靠性。
4. 利用数据统计分析数据时空特征，充分描述滑坡数据的时间和空间的特征。验证相关程度的真实性。

1.3国内外研究现状及存在的问题

本文把实测数据之间进行相关分析，不仅对不同传感器之间进行分析，对同类传感器之间也进行了分析，并结合时空特征分析进行验证相关性的准确性。

目前在国内有各种区域的滑坡因素以及各项滑坡因素的研究和分析，也形成和各样的数据研发和预警平台，形成完整的产业链。国内的研究主要注重的是预警平台的建立以及预警平台的预警预报评估方法。其主要的研究方向为地质条件和气象条件^[12]。手段多基webgis、实时降雨、集对分析等，研究的课题多为滑坡机理与因素、稳定性评价的分析、监测预报依据和建设及区域性滑坡分布及成因规律等方面^[13]。

在监测系统方面，周根平教授提出了“滑坡监测的指标体系与技术方法”^[14]，根据其方法可以得知滑坡监测系统通常监测的要素，以及使用的仪器。在滑坡位移特征方面胡显明提出“滑坡监测点运动轨迹的分形特性”^[15]，描述了监测位移数据累加值依赖于监测周期,其运动轨迹具有分形特征。同时，也有新技术的应用，即赵久彬做了大数据关键技术在滑坡监测预警系统中的应用，同系统中可以看出预警系统产生的大量数据必然会走大数据分析这一方向。而由崔云发表的《滑坡的数据挖掘方法和关键问题研究》则很好解释了滑坡数据挖掘方法^[16]。在数据分析方面由张纯志发表的《滑坡监测数据处理回归模型分析及探讨》，对滑坡实测数据进行了线性回归^[17]，初步解释了滑坡实测数据之间具有线性分布。

综上所述，滑坡实测数据缺乏关联性具体分析的科学依据，本文主要基于多数据融合下的互联网滑坡预警云系统的多源数据上进行的研究^[18]，补充滑坡实测数据在预警评估中各数据的关联性作为数据预警预报临界点的参考 ^[19]。同时具体阐述了滑坡同类传感器和不同传感器之间实测数据的关联性。

1.4研究区概况

（1）自然概况

滑坡点位于南京市浦口区老山山脉东端。中心点的地理坐标是：经度118°39’37’和经度32°09’24’。

受断裂控制的影响，在调查区西北坡上沉积了一系列的第三系砂层。20世纪70年代，该地区规模庞大。采砂活动的开采，以及大量的人工充填，增加了边坡的荷载，改变了地下水的循环条件，进入二十一世纪以后，由震旦系石灰岩、千枚岩和寒武系灰岩、白垩纪砂岩等组成。

测区附近的岩溶洞穴在试验区特别活跃的地区发育良好。土壤类型受母质影响，包括石灰土，黄棕壤和紫色土。由于土地资源的紧张，斜坡的脚已经被相继使用。

调查区气候温和，属亚热带季风气候。年平均气温为15.3°C，无霜期为228天，年降水量为1000毫米。植被类型为落叶阔叶林和常绿阔叶林。植被资源极其丰富。蕨类植物和种子共有。有148种植物。森林覆盖率为80%，森林蓄积量为330000立方米。

（2）人为活动

在土地利用过程中，坡脚为了建房使用，把多余的土堆积成了测区的坡，但由于治理不善，出现了山体滑坡。

各级政府和领导高度重视调查地区山体滑坡的危害。近年来，他们多次邀请专家到现场进行调查和了解，并投入大量财力对高风险的边坡进行调查和整治工作。但由于山体滑坡规模较大，仍有部分地区没有处理斜坡，并且在不久的将来会出现山体滑坡的新危险。 2010年10月，南京市国土资源局对山体滑坡进行了地质灾害检查。调查发现，山体滑坡群属于大型山体滑坡群，对物业造成大量威胁，是一个特大型地质灾害点。

2. Pearson（皮尔森）相关性分析

Pearson相关系数是一个线性相关系数，它也被称为Pearson积矩相关系数。用Pearson相关系数来反映两变量统计量的线性相关程度。相关系数用R表示，其中n是样本量，它分别是观测值和两个变量的均值， R描述两个变量之间的线性相关程度， R的绝对值越接近1，相关性越强^[20]。

皮尔逊的相关方法也用于社会科学，生物学，生态学和计算机科学。在这个阶段，人工智能分支下的机器学习也有使用Pearson相关进行相似性分析，以便机器执行特征学习和判断。

2.1原理

1. 协方差与Pearson相关系数

两个变量之间的相关性可以用许多统计值来衡量，最常用的是Pearson相关系数^[21]。为了理解Pearson相关系数^[22]，我们首先必须理解反映两个随机变量之间相关程度的指标——协方差（Covariance）。如果一个变量跟随另一个变量并同时变大或变小，那么两个变量的协方差就是正值，反之亦然，公式如下：

剩余内容已隐藏，请支付后下载全文，论文总字数：22285字

相关图片展示：