论文总字数：32016字

摘 要

Abstract II

第一章 绪论 2

1.1研究背景和研究意义 1

1.2国内外研究现状 1

1.2.1 风电场的概率模型 2

1.2.2 随机潮流的求解算法 3

1.3本文主要工作 4

第二章 数学原理基础 4

2.1 随机变量的描述及特征^[25] 1

2.2 几个常用的随机变量分布 2

2.3 概率密度函数的参数估计 3

2.4 本章小结 4

第三章 随机潮流的概率建模 4

3.1 风速的建模 1

3.2 Weibull分布的参数估计 2

3.2.1 利用平均风速和最大风速估计 2

3.2.2 矩估计法 3

3.2.3 最小二乘估计 3

3.3 风速随机序列生成的方法 4

3.4 风速序列与真实数据相似程度的评判 5

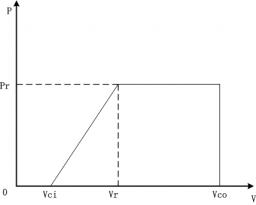
3.5 风-电转化关系 5

3.6 常规发电机与负荷模型 7

3.7 本章小结 8

第四章 基于蒙特卡罗方法的随机潮流计算 8

4.1 蒙特卡罗方法的原理 1

4.1.1 蒙特卡罗方法的精度和方差 1

4.1.2 蒙特卡罗方法的误差 3

4.1.3 蒙特卡罗方法的基本思想 4

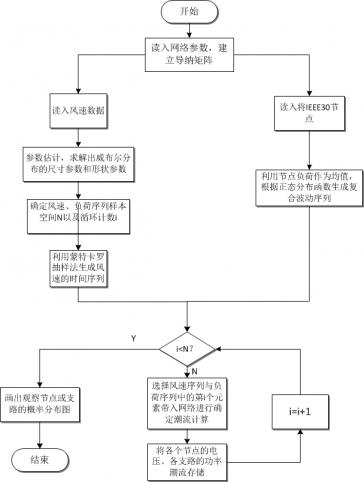
4.2 基于蒙特卡罗方法的随机潮流计算 4

4.3 基于改进算法的蒙特卡罗潮流计算 5

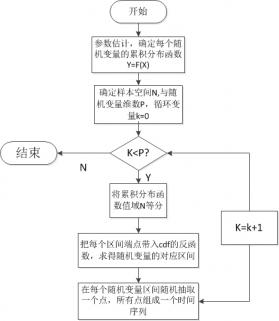
4.3.1 拉丁超立方抽样生成随机序列 5

4.4 本章小结 8

第五章 算例分析 8

5.1 风速与风力发电机出力模型建模的结果 1

5.2 各影响因素下的随机潮流计算的结果比较 3

5.2.1 考虑发电机状态的随机潮流仿真 3

5.2.2 考虑风电接入下的随机潮流仿真 4

5.2.3 蒙特卡罗抽样与拉丁超立方抽样的比较 5

5.3 本章小结 8

第六章 结论与展望 8

6.1 结论 1

6.2 展望 1

致 谢 2

参考文献 1

摘要

近几年来，风力发电在全国范围内得到了大力发展，并且风力发电的装机容量逐年递增。尽管风力发电不会引入污染，但是由于其的出力的随机性，风电的引入会对调峰、电能质量以及系统稳定性带来影响，再加上电力系统中原本就存在如运行方式改变、元件故障或检修等诸多不确定性，继续使用常规潮流计算会有很大的误差。针对这个问题，本文提出了一种基于蒙特卡罗方法的随机潮流计算，以求能更好地反映大规模风电接入下的电力系统的电压、潮流分布。

本文首先对电力网络中的不确定行进行建模，考虑了大规模风电接入下的风电场的概率模型；负荷波动模型以及常规发电机组的故障模型；风电场的概率模型通过威布尔分布对风速建模，之后利用风——电功率转化关系得到风电场的出力的时间序列；负荷建立的是正态分布模型；常规发电厂用二项分布建立模型。

将随机变量引入系统中后，本文使用了蒙特卡罗算法来求解随机潮流。蒙特卡罗法有着很好的普适性以及准确性，求解过程不受问题复杂程度以及规模的影响。但是蒙特卡罗方法需要大量抽样，因此效率并不高，所以本文提出了拉丁超立方抽样来提高其抽样效率，拉丁超立方抽样可以利用少量的抽样点就还原出样本特征，因此能大幅减少抽样点数，节约算法时间。最后结合IEEE30节点，在考虑各种不确定性的影响下验证了蒙特卡罗算法的准确性和改进抽样算法的准确性以及快速性。

关键词：随机潮流计算，威布尔分布，蒙特卡罗方法，拉丁超立方抽样

Abstract

In recent years, the wind power generation has been well developed in the whole country, and its installed capacity is still increasing. Although wind power generation doesn’t cause pollution, the introduction of wind power will influence on the regulation of system load, power quality and stability of the system ,which is due to the randomness of its output power performance. Besides, some other randomness originally exists in power system, such as the change of operation, the fault or recondition of power elements. All of that randomness will cause unacceptable errors if we still use the conventional power load flow method. In this case, this paper proposes a probability power flow method which is based on Monte Carlo Method,to make a better description of the distribution of load power and note voltage in a system connected to large-scaled wind farms.

Above all, this paper model the randomness in the system, take the probability models of large-scaled wind farms, load fluctuation and the faults of conventional power generators into account. The randomness of wind speed are accepted to conform to the Weibull distribution. After the models of wind speed have been set up, it can be transfer to the time series of output power of wind farms via wind speed-power relation; the loads conform to Normal distribution and conventional generators conform to the Binomial distribution.

Once all the probability models have been set up, the probability load flow of the system can be solve by the Monte Carlo Method. The Monte Carlo Method is universally feasible to all kinds of problems and the result can be adequately accurate. Mean while, the procedure will not be affected by complexity of the problem. However, to make the result accurate, Monte Carlo Method needs huge quantities of sampling points which decrease is efficiency. To raise its efficiency, this paper introduce Latin Hypercube Sampling Method. This method can describe the characteristic of the cumulative distribution functions of multidimensional random variables with little sampling. At last, this paper verifies the accuracy of Monte Carlo method’s result and the rapidity and as well the accuracy of Latin Hypercube Sampling Method.

Keywords:power load flow method, Weibull distribution, Monte Carlo Method, Latin Hypercube Sampling

第一章 绪论

1.1研究背景和研究意义

能源是社会进步所离不开的助力与基础。但是，现如今，化石能源的储量越来越少，并且这些不可再生资源总会枯竭，而努力缓解能源稀缺而带来的压力、寻求可再生能源作为替代并最终实现能源的可持续发展也成为世界各个国家的重大能源战略。

经过近数十年的努力，依靠着材料、动力、控制策略与互联网技术等科技最新成果，风力发电的技术越来越成熟、控制越来越可靠、功率越来越大、成本越来越低。与其他常规的发电方式比如火力发电相比，它的建设的工期一般比较短；装机规模可大可小，非常灵活，并且也可以根据资金宽裕程度来调整；风力发电机运行简单，通常是无人值守的；而风力机的占地面积却相对较小，建设装机时不需要非常良好的建筑环境，甚至在丘陵地区、海岸、河岸、戈壁等复杂地形下均可建设。这些非常实用并且突出的优点，让风力发电成为上述几种新能源中最热门、拥有最成熟的理论实践依据、最能进行大规模建设即有良好商业化发展前景的发电方式^[1]。

我国近几年来风力发电的发展很快。2014年一年的风机的装机容量的增幅更是创下了历史新高。全国新增的装机机组共有13121台，总容量达到23196MVA。并且除了东北地区，西北、西南、华北、华东地区的装机容量都大幅增加，其中以甘肃、新疆的增幅最大。另外，我们国家在海上也加紧了风电的开发，去年我国海上新增61台装机，总容量为229.3WM，增幅接近五倍^[2]。

风力发电完全无污染是我们大力发展的原因，但风电场的有功出力会随着天气情况的变化而起伏，这将会给大电网带来很大的随机波动。在电网看来，可以把接入的风电当做是一个随机扰动。大规模风电接入电网的情况下会给电网引入大量谐波，并且电压会出现上下波动，线路之间的潮流分布也不再是确定的数值^[3]。电网中这些随机性会降低电网的稳定性，并且使发电厂发电厂制定发电计划以及电网的运行调度遇到困难。同时，风电的接入还会对系统的调峰调频带来影响^[4]。在这种情况下，要使用确定潮流计算，就必须考虑对所有的随机变量的每一种状态的组合都进行一次运算，这无疑使得计算量很大。

为此，本文引入随机潮流来描述大规模风电接入电网下电网的电压、功率潮流的分布情况。随机潮流计算的结果可以很方便地展示节点电压和线路功率潮流的过限率，从而进一步地得到大量随机变量的情况下电网运行指标。这些指标可以应用到如下方向^[5]：

(1) 规划问题：电力系统的规划需要潮流计算作为参考依据和验证，在大规模风电接入以及诸多不确定因素的情况下，随机潮流能够更好地描述系统的状态。

(2) 运行问题：包括调度分配、以及考虑电力市场作用的发电、电网以及负荷之间的互动问题^[6]。

(3) 其他诸如最优化潮流^[7]，风险评估^[8]等等。

1.2国内外研究现状

在生产实际中，潮流计算不仅在系统稳态运行时是了解各地运行情况的重要依据，在发生故障时也是进行故障类型、地点判断的基本运算，而且是电网做长期规划、设备选型最终验证方案正确性的基础。

常规的潮流计算认为网络中的各个参数都是确定的，包括网络拓补、发电机出力与负荷情况等等并以此来求解节点电压与各条支路的功率潮流。然而，在实际运行过程中，整个电网充满了不确定性，比如负荷是无时无刻不在变化的，网络拓补可能会因为运行情况的变化而发生变化，同时网络里还可能出现故障，有些设备要退出运行。这些都会对潮流计算的结果造成影响，如果不加以考虑，我们得到的计算结果会与实际情况有较大的误差。

电网中的不确定因素主要表现在：

(1) 供电局或是设计院在做电网规划的时候一般都是要考虑未来十几年乃至于几十年该地区的用电情况，包括发电、用户用电、网络建设。但在经济的高速增长，长期的规划很难做到精确。

(2) 国家电力行业产业现在逐步进行改革，整个行业从原来的统一管制到将来引入市场机制，电网的建设和运行机制会出现越来越多的变数，这也会导致电网在未来运行中的不确定性进一步加强。

(3) 而在用户侧，用户更关心的是电价对其造成的经济影响^[9]。用户可能会选择其最有利的电价环境下用电。居民用电的价格相对便宜，而工业、商业用电的价格相对较高，而本身需要赢利的工厂、商家就不得不考虑在一个电价相对较低的时段进行更大规模的生产，这无疑会对电网的运行引入变数。

(4) 电力系统在运行的时候设备可能出现故障，亦可能需要退出运行进行检修，这都是网络的不确定性。

(5) 现如今，国家大力推进新能源技术的发展，以风力以及太阳能发电代表的新能源具有清洁环保的有点。但很多新能源也伴随着发电能力依赖于天气情况等随机因素，导致在电源端可能出现很强的随机性。

针对以上情况，如果就每一种情况都进行建模、确定潮流计算，无疑需要极大的工作量，并且需要的时间会很长，跟不上系统要求的快速响应的要求。因此，我们引入随机潮流来解决这个难题。

1.2.1 风电场的概率模型

在求解电力系统随机潮流计算时，根据系统中的随机变量是否考虑其时序，可以分为序贯仿真、非序贯仿真^[10]。

非序贯仿真不考虑随机变量的时序性，又被称为状态抽样法。这种方法的可靠性根据抽样次数来判断，并被广泛运用在电力系统分析当中。我们知道，系统状态是系统中各个部件的状态的组合，每个部件的状态都是一个随机变量，可以依照其处于某种工况下的概率利用抽样的方式来得到。由于非序贯仿真不需要考虑随机变量的时序性，所以计算量很小，计算时间很短，可以用来模拟系统中发电机故障这一不确定性。

剩余内容已隐藏，请支付后下载全文，论文总字数：32016字

相关图片展示：