论文总字数：47780字

摘 要

潮流计算是电力系统分析中最基础的一个部分，配电网的潮流计算则对配电网调度和安全运行有很重要的作用。而配电网的本身结构了决定了它不能够直接使用传统的潮流计算方法，需要进行三相潮流计算。并且基于新能源的分布式电源具有发电波动性与随机性特点，出力较难得到一个准确值，所以整个系统是具有不确定性的。

本文则对包含不确定性的配电网系统的潮流计算进行了研究。首先本文对不确定性的信息进行了处理，将其表达为区间量的形式，并提出了仿射计算来改进区间计算的保守性。然后对配电网系统中的线路，并联电容器组，非分布式电源等元件进行了三相建模，并把风机转化为了可以直接进入潮流计算的区间值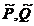。最后提出了用前推回代法进行潮流计算，对IEEE33节点系统进行了数据仿真，证明了本文提出的算法是可行的，准确的；而且对仿射计算和区间计算进行了对比，证明了基于仿射计算的配电网区间潮流计算得到的结果区间宽度是要比区间计算小的；最后用前推回代法对IEEE33节点的缺相系统进行仿真，证明了该算法可以在不对称运行的情况下进行配电网区间潮流计算。

关键词：配电网潮流计算 分布式电源 前推回代法 区间计算 仿射计算

ABSTRACT

The power flow analysis is the most fundamental part of power systems analysis, while the power flow calculation of distributed power systems is very essential for distributed systems safe running and managing. And due to its structure, the traditional power flow algorithm can not be directly used in distributed power flow calculation, which means that people need to take three phase into consideration. And with the development of distributed generators, the distributed power systems contains more and more uncertainties. Because distributed generators are intermittent and random and its outputs are depended on real conditions.

This paper concentrates on the power flow analysis of distributed power system which contain uncertainties. Firstly, this paper comes up with interval math to describe uncertainties and compares interval algorithm and affine algorithm. And this paper gives the three-phase models of elements in distributed power systems such as lines and an interval outputs of wind generators denoted as 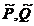. At last, this paper uses IEEE33 system to test and verify the correctness and effectiveness of algorithm; furthermore, it compares the results of interval algorithm and affine algorithm and verifies the algorithm can be used in unbalanced running.

Key words: power flow analysis, distributed generators, interval algorithm, affine algorithm

目录

第一章 绪论 1

1.1 研究背景 1

1.1.1 主动配电网 1

1.1.2 配电网潮流计算与传统潮流计算区别 2

1.2 考虑不确定性的配电网潮流计算研究现状 2

1.2.1 三相配电网确定性潮流算法 2

1.2.2 配电网概率、区间、模糊潮流计算目前研究 4

1.3 本文所做的工作 6

第二章 区间数学理论基础 7

2.1 区间数的基本理论和区间计算 7

2.2区间计算的保守性问题 8

2.3 仿射计算 9

第三章 配电网系统三相建模 12

3.1 线路的三相建模 12

3.2 并联电容器的三相建模 13

3.3 非分布式电源的三相建模 14

3.4 负荷的三相建模 15

3.5 风电机的三相建模 16

第四章 配电网三相区间潮流计算 18

4.1 基于区间计算和前推回代法的配电网潮流计算 18

4.2 基于仿射计算和前推回代法的配电网潮流计算 20

第六章 结论 27

致谢 28

参考文献 29

附录 31

绪论

1.1 研究背景

1.1.1 主动配电网

随着化石能源的逐渐枯竭，对环境污染与气候恶化所产生的严要影响，太阳能以及风电、光伏等可再生能源等新型发电技术的发展，分布式能源已经成为了人们未来发电的最佳选择。灵活、经济与环保是分布式发电技术的主要特点, 然而受地理条件、天气情况和外部环境等因素的影响，这些可再生电源的能量输出具有间歇性和随机性，对其发电量的预测也比传统发电方式预测复杂，通常这些可再生能源的输出通常是一个不确定的输出，也就是包含不确定性。

常用的分布式能源有内燃机，燃料电池，微型燃气轮机，光伏电池，风力发电机等。在某些特定地理环境中，还可以采用诸如地热发电，潮汐能发电等技术。本文主要对风力发电机组进行分析，所以仅介绍风力发电。

风力发电技术是将风能转化为电能的发电技术，也是一种清洁能源。和光伏电池类似，它的输出功率由风能决定。风力发电机可采用同步电机、感应电机、或者直流电机。由于其输入功率存在固有的不平衡性，风力发电在一定程度上可起到储能作用，有的风力发电机输出的交流电经过整流后向蓄电池组充电，然后通过逆变器连入电网。

目前对分布式发电的研究工作可以主要分为硬件与系统两个方面。硬件研究包括：分布式电源的研究，电力电子转换接口的研究，电能存储系统的研究，和分布式发电系统实验室的建设。其中，对分布式电源的研究集中于电机设计方面，主要目的是降低电机成本。而对分布式能源的系统研究包括：分布式发电系统的规划，分布式发电系统的稳态分析和分布式发电系统的暂态分析。

而对于配电网其本身来说，配电网的自身系统中也包含了许多的不确定性信息。比如系统中每个负荷节点的负荷量在每个时刻都是不一样的，根据负荷预测，只能说负荷的波动是在某一个确定的范围内，但并不能得到准确的负荷值；其次，由于配电网的线路是开环运行的，当供电方向发生改变的时候，或者当线路进行常规检查的时候，网络的连结运行方式都会发生改变，因此配电网本身是具有不确定性的。对于负荷的不确定性，目前只能通过大量的历史数据来进行负荷预测，从而得到一个负荷的变化范围。通过该变化范围，可以得到负荷不确定性的概率分布或隶属度函数。

1.1.2 配电网潮流计算与传统潮流计算区别

当在进行常规的高压输电网的潮流计算的时候，普遍采用的是牛顿-拉夫逊算法及其变种。这些算法已经被证实其正确性和优越性，并成功的被人们广泛利用于输电网络的潮流计算当中，特别是环状结构的高压网络中。对于规模比较大的系统来说，牛顿-拉夫逊算法存在一定的问题，主要是因为牛顿-拉夫逊算法其本身需要求解非线性方程组的雅克比矩阵，而对于大规模的系统来说，利用牛拉法进行计算，由于节点众多，非线性方程组中的未知量众多，这一点导致了雅克比矩阵的阶数必然增多，而迭代过程中，每一次迭代都需要求解雅克比矩阵和线性修正方程的值，因此为了减少牛顿-拉夫逊算法的工作量，在潮流计算中通常做出如下的一些假设：

首先高压输电网络中各元件的电抗一般远大于电阻（即）。各节点电压幅值的改变主要是影响网络中的无功分布，而有功功率分布主要决定于节点电压的相角。因而可以将牛拉法的修正方程解耦；

使得雅克比矩阵中的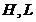阵化为常数阵，这是由于默认两个节点之间的电压相位的变化并不大。

传统的牛顿-拉夫逊算法及其变种主要面对的对象是高压输电网，而对于配电网来说，配电网的电压等级普遍低于或等于35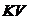，并且配电网的另外一些不同的特征，使得牛顿-拉夫逊算法及其变种在配电网潮流计算中无法很好的运用，因此需要对牛顿-拉夫逊算法及其变种提出一些新的要求：

首先，是否能够收敛在配电网系统的潮流计算中比传统的潮流计算中更为重要。这是由于配电网都是闭环设计, 开环运行，因此, 线路供电容量差别较大, 使得整个配电网中线路参数差别也较大, 比值的范围较宽, 而且一般比值较大，使得原来在高压输电网中行之有效的算法不能使用，其次要计算三相的情况。

因此，在计算配电网的潮流的时候，很难能够直接应用在输电网中证明其有效性和实用性的一些已知算法，对配电网潮流计算的算法提出新的要求。

1.2 考虑不确定性的配电网潮流计算研究现状

1.2.1 三相配电网确定性潮流算法

目前能够成功利用于三相配电网潮流计算中的已知算法主要有如下几种：

1. 前推回代法

前推回代法类似于手算潮流，通常系统都已知了根节点的电压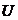，以及每一个节点的确定性负荷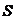，还有配电网网络的结构图以及每一个支路的阻抗。而需要求得每一条支路上的功率和各个节点的节点电压。它的基本思想是基于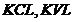定理，当进行第一次迭代时，假设系统网络上的每一个节点电压保持恒定，该电压为根节点的电压，然后从线路的最后一个节点根据电压幅值和节点负荷开始依次计算每个节点的出端电流和进端电流，该过程中只考虑了网络中的功率损耗，而电压保持不变，由此可以得到根节点的功率。再根据根节点的电压和回推过程中得到的根节点功率，依次计算每一条支路上的电压损耗，由此得到每一个节点的电压幅值。反复的进行这个过程，一直到满足收敛条件。

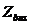1. 高斯法

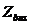高斯法主要是通过下述公式来求解配电网网络方程：

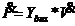(1-1)

其计算过程利用了叠加原理，考虑两种节点：源节点与其他节点，分别通过公式求得当源节点单独作用时候的各节点电压和支路电流；以及切除源节点后，各节点电压和支路电流，然后将其叠加，完成潮流计算。

3）网络化简法

网络化简法的主要原理是将网络中非线性的元素进行相应的线性化，首先根据线路的初始条件将系统中非线性的元素线性化，然后在每一个节点寻找驱动点线性值，再由此计算出电压电流。

1. 直接法

对于配电网络来说，其拥有独特的树形结构，根节点就是供电节点。配电系统可以利用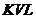直接写出一串等式，这些等式包含了供电节点。如果负荷不是表示为恒定的电阻而是恒定的复功率的话，那么配电网潮流计算的问题就可以转化为简单的电路问题：

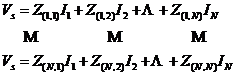(1-2)

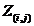式中，是节点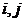之间的阻抗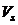，是已知量。

上述方程可以通过支路电流直接求解。

1. 牛顿法和改进牛顿法

牛顿法和传统潮流计算中一样，通过非线性方程组的雅可比矩阵求解修正量，不断对初始值进行修正，最终得到待求量，这里不再进行叙述。

改进牛顿法是对配电网潮流计算进行了如下两点假设：

1. 相比输电网络来说，配电网络中，每一条支路的长度很短，功率很低。并且总的长度相比输电网线路长度来说，也很小，因此在线路上的电压降落可以忽略不计。
2. 配电网是树形结构，不存在或存在极少环路。

于是可以对雅可比矩阵中的元素进行化简，从而得到其简化形式。

1.2.2 配电网概率、区间、模糊潮流计算目前研究

可再生电源的能量输出具有间歇性和随机性，必须考虑不确定性问题。对于电力系统中的随机性的信息，目前主要有三种描述方式：区间潮流，概率潮流，模糊潮流。但是上述的三种方法都存在其本身的弊端。概率理论无法处理那些不具有随机性特性的信息，而且概率理论的计算量很大。而模糊集理论由于存在人为设定的成员函数，因此从一定程度上来说，模糊集理论受到人为的干预，况且模糊集理论在细致刻画问题的同时，也使问题复杂化。而相反区间数学使得问题过于简单化，很多节点负荷的边界是模糊的、不确定性的。因此选择一种合适的方法来描述信息的不确定很重要。

剩余内容已隐藏，请支付后下载全文，论文总字数：47780字