论文总字数：23987字

摘 要

本文对柔性球体碰撞接触的相关问题展开研究。首先选取铅质球体为仿真对象，利用有限元模拟，分析它在接触压缩甚至碰撞中的变形行为，并将所得的结果与Hertz理论的计算结果作对比，最终得出结论。另外，推导了弹性球体碰撞问题中的动荷系数，并有数值模拟证明其有效性。最后，又模拟乒乓球受刚性平面压缩变形时的复杂变形行为，并将结果与实验实测作对比，借此研究薄壁空心球结果的压缩失稳模型。

通过本文的研究，进一步证明了数值模拟技术在接触力学中的重要作用。另一方面，本文开创性地将动荷系数推广到柔性球体与刚性平面的无摩擦接触问题中，为以后此类问题的解决又添一个有效的手段，并为动荷系数法的应用拓宽了领域。最后，本文对薄壁空心球的相关研究增进了我们对其变形行为的认识，为更好地利用这类材料提供依据，同时为数值模拟方法解决此类问题提供一个计算平台，供以后的研究者参考。

关键词：接触、碰撞、有限元、Hertz理论、动荷系数、薄壁空心球结果

A STUDY ON THE CONTACT OF A DEFORMED BALL

WITH 3D NUMERRICAL SIMULATION

Abstract

In this paper, the problem of the collision contact of deformed spheres is studied. Firstly, lead ball is simulated with finite element method (FEM) and compared with the result from Hertz theory to evaluate the effectiveness of FEM. Besides, dynamic load coefficient is extended to the collision of a deformed ball. We can prove it effective in such problem with the simulation by FEM. In addition, Thin-walled hollow spheres is studied in this paper. Simulation by FEM shows the patterns of sphere’s deformation. The result from FEM is compared with that from experiments to inquire the mechanical properties of porous material.

Through the research of this paper, the important role of the numerical simulation technology in contact mechanics is proved. On the other hand, the dynamic load coefficients creatively extended in this paper will provide another way to solve the collision problem of a deformed ball. Finally, FEM used in the study of thin-walled hollow spheres could offer future researches a reference.

Key Words: Contact、Collision、FEM、Hertz theory、Dynamic load coefficient、Thin-walled hollow spheres

目 录

摘 要 I

Abstract I

第一章 绪 论 1

1.1 引言 1

1.2 接触力学简介 2

1.2.1 经典接触力学 2

1.2.2 非经典接触力学 2

1.2.3 计算接触力学 3

1.2.4 实验接触力学 3

1.3 分析碰撞接触问题的一般方法 4

1.4 多孔轻质结构材料介绍及研究现状 5

1.5 本文的研究目的和主要研究内容 6

第二章 柔性球体碰撞问题的数值模拟研究 8

2.1 简介 8

2.2 研究方案设计及可行性研究 9

2.3 实心球静态接触问题研究 10

2.3.1 静态接触问题的数值模拟研究 10

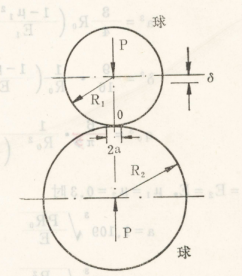
2.3.2 静态接触问题的Hertz解法 12

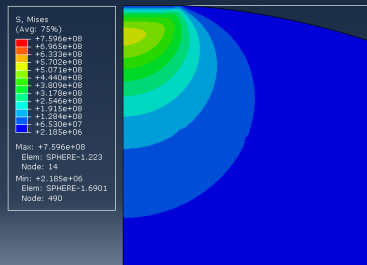
2.3.3 静态接触问题结果分析 13

2.4 实心球动态碰撞问题研究 16

2.4.1 动态碰撞接触问题的数值模拟研究 16

2.4.2 动荷系数计算碰撞问题 17

2.4.3 动态碰撞问题结果分析 19

2.5 薄壁空心球压缩变形问题研究 21

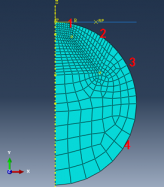
2.5.1 空心球结构受接触压缩时的有限元分析 21

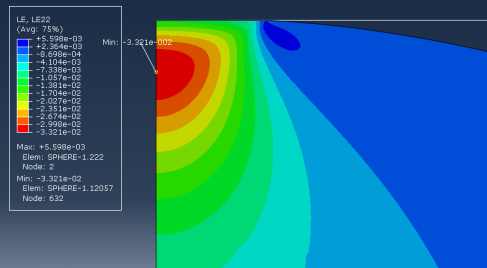
2.5.2 薄壁空心球结构接触问题的结果分析 23

第三章 全文总结与展望 28

【参考文献】 29

致谢 31

第一章 绪 论

1.1 引言

碰撞接触在我们的生活中随处可见：小到运动员将时速100km的乒乓球打向球台，大到陨石飞向地球时展现出的绚丽流星雨。作为常见的运动形式，碰撞接触问题也受到古往今来的科学家们的重视。

然而在力学中，接触问题却并没有得到全面的解决。接触时的力学测量一直是实验力学中的难点。首先，接触问题无法用常规的电测手段解决，因为表面的应变片会因为物体的接触而失效，而内部的植入式应变又无法测量出接触面的应力应变变化。光测手段却会因为接触材料的阻挡而只能对特殊的透明材料进行测量。

理论研究方面，Heinrich Rudolf Hertz在接触力学领域作出了开创性的突出贡献，提出了弹性变形阶段的Hertz理论。随后由其他人完善的接触力学理论是涉及到接触体的各种科学及工程研究中不可缺少的工具之一。但这些理论大都停留在弹性阶段和理想弹塑性模型，伴以各种各样的简化假设，并且只有模型足够简单的某些经典问题才能得到精确的解析解。

计算机的发展无疑为此类问题的解决提供了新的思路。有限元和有限体积法的提出让计算机解复杂微分方程成为可能。而随着计算机性能的日益提高，计算机数值模拟技术在各种复杂的工程问题中显得越来越重要。

所以，针对以上传统力学手段在处理碰撞接触问题时的困难，利用数值仿真模拟技术无疑是一个新的有效手段。但是，针对碰撞接触这一类高度非线性的变形行为，仿真过程也并不容易。尤其当模拟的是大变形行为时，那么将包含几何非线性和边界非线性甚至是材料非线性三种非线性过程，结果并不一定可信。

本文就将针对上述些问题展开研究，利用有限元分析，模拟柔性球体与刚性平面接触受压时的变形行为，分析其压缩力学性能，并将结果与理论和实验结果对比，分析得出结论。

另外，对乒乓球的研究同时还可以为分析薄壁空心球的压缩力学性能提供平台。这类的薄壁空心球结构是能够充分利用材料的力学性能的一种最基本的子结构之一。利用空心球烧结的空心球泡沫材料就是一种典型的有着良好力学性能的多孔材料。这类多孔材料被广泛应运于多个行业。所以，分析多孔材料的基础子结构——空心球的力学性能也就显得尤为重要。因此，对乒乓球压缩力学性能的分析同样也具有深远的工程实用意义。

1.2 接触力学简介

接触力学问题可以说是开始于Heinrich Hertz在1882年发表的经典论文——《On the contact of elastic solids》^[1]。当时Hertz年仅24岁，并在柏林大学做Helmholtz的研究助理。他对这个问题的兴趣是由玻璃透镜间的光学干涉实验引起的。为了保持住玻璃透镜而施加在上面的接触力所引起的弹性变形是否对干涉条纹的图案产生重要的影响，这一问题吸引了Hertz的注意力。他在对干涉条纹的观测中得出了接触部位的椭圆区域假说。静电势理论方面的知识使得他可以通过类比展示出接触压力的椭圆赫兹分布。这样的接触压力可以在两个接触体上产生弹性位移，并在所提出的椭圆接触区域是相协调的。最终，Hertz提出了他的理论，并于1881年1月撰写成论文提交给柏林物理学会。

然而，Hertz理论只适用于无摩擦的表面和完全弹性体。接触力学在20世纪下半叶的发展，很大程度上就可以说是在除去这两个限制方面所做的进步。对接触体接触部分摩擦力的合适处理，就可以把弹性理论扩展到实际情况中两物体接触时所发生的滑动和滚动摩擦。与此同时，塑性理论和线性粘弹性理论的发展，使得接触问题中应力和变形可以丰富到非弹性体中。

1.2.1 经典接触力学

在接触问题中，对Hertz理论中的两个假设（无摩擦、纯弹性）的研究，发展出了经典的弹性接触力学。经典接触力学就是以Hertz所开创的理论及其相关解决方法为基础。然而，其发展确是相对很缓慢的。直到约一个世纪之后，Johnson、Kendall和Roberts才找到一种近似的方法处理两个弹性体的粘着接触问题^[2]。20世纪中叶，谈论接触力学领域的发展就不得不提及Bowden和Tabor。Bowden和Tabor首次强调了接触中物体表面粗糙度的重要性，考虑表面粗糙度重新处理接触问题时发现，存在这种表面摩擦的接触体之间的真实接触面积要小于表面接触面积^[3]。他们的研究也派生出了几种粗糙表面的接触力学理论。另外，Archard 在1953年的文章也在此领域做出了突出贡献。通过他的研究，粗糙的弹性表面间，接触面积与法向力接近比例关系^[4]。

1.2.2 非经典接触力学

虽然经过很多科学研究者的努力，但经典的接触力学解决方法任然有太多的限制，只能求解一些几何形状比较规则的物体，应用范围非常有限，无法处理实际生活生产中的接触现象。最近的半个世纪内，数值解法蓬勃兴起并得到了长足发展。这也为接触问题提供了新的数学求解工具。数值解法只能得出所处理问题的离散的结果数据集合，得不出完整的函数关系。但对于实际工程问题，这样的方法已经有足够的实用意义。

众多的数值解法中，有限元法发展得最快，应用的范围最广，也最成熟。二十世纪五十年代，处理固体力学问题时，有限单元法首次被提出，随后又经历代科学家丰富完善，并最终成为众多领域处理各类问题不可或缺的技术手段^[5]。而在接触力学中，有限元法也自然扮演着重要的角色。1970年，Parson和Wilson在处理二维弹性无摩擦问题时首次使用了有限元解法^[6]。Kikuchi和Cheng用增量形式研究大变形的摩擦，讨论了各种情况下摩擦接触的增量规律。他们用现代化的Lagrange关系式,根据虚功原理，由大变形的Prandtl-Reuss的应力应变关系式，写出拟静力学的增量平衡方程，最后得到用于有限元法的矩阵方程,给出了数值解^[7]。在处理边界条件方面，最有影响力的就是将接触转化为最小值约束问题的思想。而解决这种最小值的方法，就不得不提到Oden和Ohtakate所建立的罚有限元方程^[8]。这项工作，将约束变分问题转化为罚优化问题求解，减少了计算量，并最终很好地解决了弹性接触问题。

1.2.3 计算接触力学

20世纪末计算机的飞速发展，更加促进了数值解法在接触问题中的应用。甚至发展出了更具生命力的分支——计算接触力学。大量发表的著作显示，这种解决方法几乎可以解决一切的接触问题^[9]。

为了提高计算接触问题的有效性、可靠性、精确性和稳健性许多大型通用程序编入多个接触计算方法和算术，因此计算接触问题的能力大大加强。不仅能够计算弹性体和刚体，弹性体与弹性体之间的接触，也能够计算非弹性体之间的接触，更能有效地计算接触面之间有摩擦的问题。在了解粗糙表面的变形行为时，计算接触力学被广泛使用并能得出满意的结果。Kuchaski等人分析了弹塑性球和一个刚性平面之间的接触，并得到了载荷和接触面积的关系^[10]。Liu等人开发了一个等温弹塑性粗糙模型，并用单纯型算法的增量形式求解圆柱与刚性平面的接触问题^[11]。而Lipo Lin和Jenfin Lin利用有限元计算软件创建了新的模型，为确定在两个表面接触时粗糙球面的弹塑性规律提出了一种新的方法^[12]。

计算接触力学的发展，促进有限元法和有限元法为基础的工程分析系统的发展，同时也促进了接触力学本身和固体力学的发展。

1.2.4 实验接触力学

接触问题一直是实验力学中的难点之一。然而，20世纪80年代左右，用实验方法处理接触问题有了重大的突破。这一突破仍然归功于计算机的发展，使得一项新的技术得以面世——三维数字图像相关技术。三维数字图像相关技术是一种基于双目立体视觉原理和数字图像相关匹配技术的方法^[13]。由于数字图像相关技术具有非接触、全场、高精度测量等优点，所以被广泛用于接触实验中材料接触受压时的全场变形测量。尽管如此，这项手段也只能用于某些特殊的透明材料间的接触实验。

另外，借助于多项实验器材的面世（原子力显微镜，摩擦力显微镜和纳米压痕仪器），原子级摩擦过程的实验方法也得到了长足进步。这些实验仪器可以通过材料在加（卸）载时的位移——载荷关系得出其硬度和弹性模量等力学性能^[14]。所以，这些实验手段也可以很好地测量材料在接触载荷条件下的变形行为。

除此之外，还有一些研究者发明出天平称重法和复写纸压痕法，来测量微小颗粒间复杂的碰撞接触问题^[15]。

1.3 分析碰撞接触问题的一般方法

剩余内容已隐藏，请支付后下载全文，论文总字数：23987字

相关图片展示：