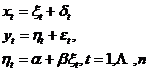论文总字数：19759字

目 录

摘要 1

Abstract 2

一、引言 3

二、正态混合尺度分布 4

2.1多元t分布（T-SMN） 5

2.2多元slash分布（S-SMN） 5

2.3污染正态分布（CN-SMN） 5

三、SMN-RMEM的估计 6

3.1重尾重复测量误差模型 6

3.2 EM算法简介 6

3.3参数估计 7

四、局部影响分析 8

4.1 Hessian矩阵 10

4.2常见的扰动模型 11

4.2.1 似然加权扰动 11

4.2.2 响应变量的扰动 12

4.2.3 方差加权扰动 13

五、应用 13

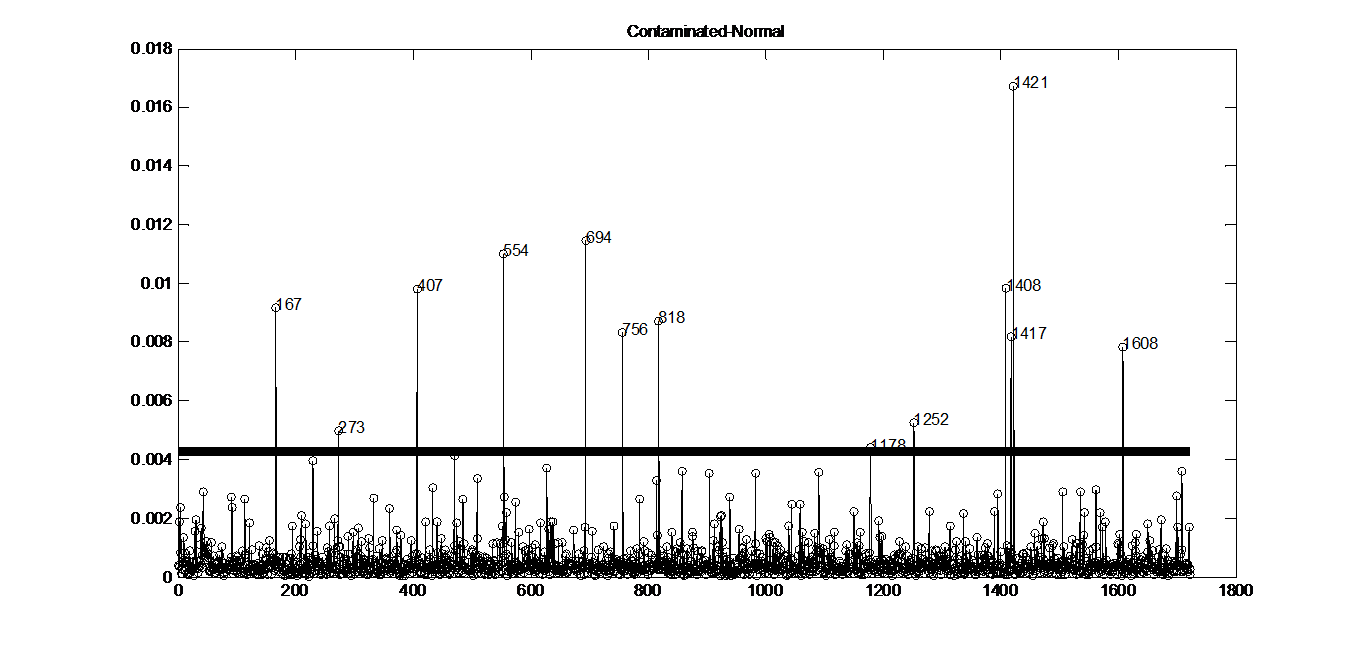
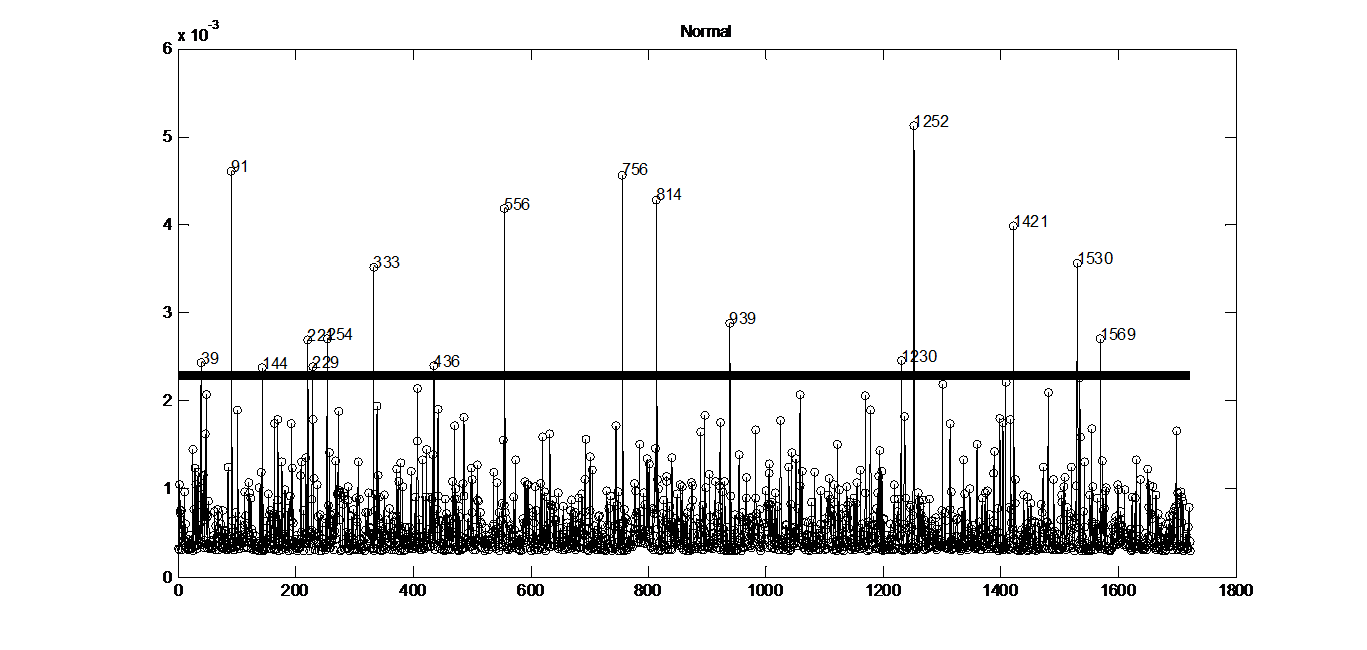
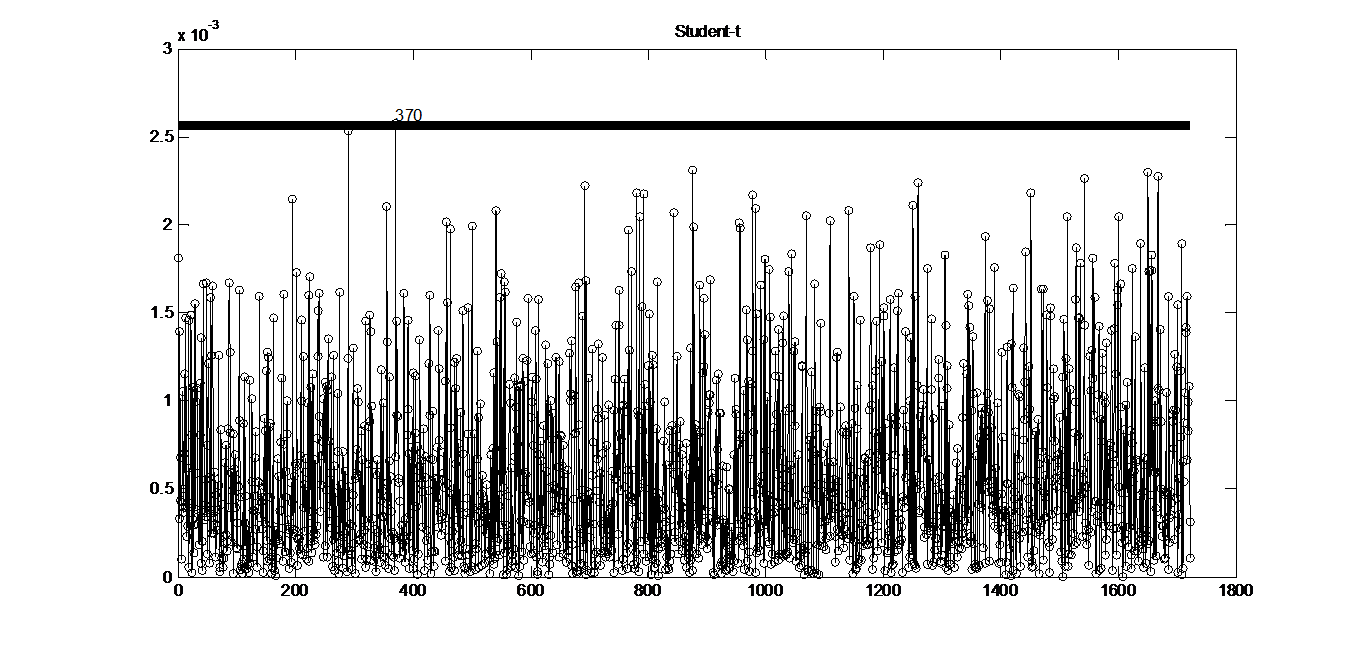
5.1 三种扰动模型 14

5.2 对比分析 21

六．小结 22

参考文献 22

致谢 25

重尾重复测量误差模型的估计和局部影响分析

卢晶晶

，China

Abstract Measurement error models are frequently used in various scientific fields,such as engineering, medicine, chemistry, etc. In this work, we consider a new replicated structural measurement error model in which the replicated observations jointly follow scale mixtures of normal distributions, which called SMN-RMEM. Scale mixtures of normal distributions form a class of symmetric thick-tailed distributions that includes the normal one as a special case. Maximum Likelihood estimates are computed via an EM type algorithm method.The local influence method is used to assess the robustness aspects of the parameter estimates under some usual perturbation schemes. However, as the observed log-likelihood associated with this model involves some integrals, Cook’s well–known approach may be hard to apply to obtain measures of local influence.Instead, we develop local influence measures following the approach of Zhu and Lee, which is based on the EM algorithm. Results obtained from CSFII data set are reported, illustrating the usefulness, relative simplicity, and practical adaptability of the proposed methodology.When a small disturbance occurs in the model or the data, the local influence analysis can compare the variation of the estimated quantity before and after the disturbance.The results of s data set local influence analysis confirm the robustness of SMN replicated measurement error model, compared to the normal ones.

Key words：EM algorithm ; Measurement error ; Replicated measurement; Scale mixtures of normal distribution; Local influence analysis

一、引言

在经典的统计研究中，通常认为回归模型中的协变量或者解释变量，可以通过观测准确所得。但是，当认为变量的观测值与变量的真实值是存在测量误差时，该假设是很难成立的。显然，忽略该误差将导致回归系数的估计有偏。如经典回归模型中一个更为真实的代表，在测量误差（变量中的误差）模型中，假定独立的变量是服从于误差项的。Fuller(1987),Cheng和Van Ness(1999)以及Carroll等人对测量误差模型（Measurement Errors Models，简记为MEM）进行的全面性研究。

线性测量误差模型表示如下：

（1）

其中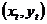为观测值，等于真实值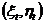加上测量误差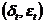。变量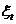可以被视为固定的未知参数（功能模型），或作为独立同分布的随机变量（结构模型）。在本文中，我们主要考虑结构类的模型。Reiersol(1950)表明，在正态性条件假设下，除非有关于参数进一步的信息，否则该模型是不可识别^[4]。因为我们不可能只是关于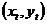的分布函数或者模型的参数之间建立单一的关系。解决该问题的一种常见的方法是Cheng和Van Ness(1999)提出的，对误差变量作出先验性分布假设^[2]。然而在重复测量误差模型中，不可识别的问题将不复存在，并且通过重复测量所得的数据可以对误差项进行估计。Chan和Mak (1979)^[5]以及lsogawa (1985)^[6]解决了在正态分布下重复测量结构模型的极大似然（ML）估计。近期，同样是在正态分布下，Lin等人^[33]（2004）推导出一种迭代的EM算法来计算重复模型中的极大似然估计^[7]。但是，在参数估计中正态性假设对于并非总是可靠的，以及当出现异常值时参数的估计是缺乏稳健性的。重复测量误差数据下需要开发更多的稳健模型，Lin和Cao^[23](2013)提出了重尾分布下的重复测量误差模型，并给出了该模型下的参数估计。

在本文中，我们主要是在混合尺度正态分布(Andrews^[8]和Mallows 1974^[9])假设下，检验出重复测量误差模型中的强影响点和异常值点。Fang等人^[10](1990)提出作为椭球对称分布一个非常重要的子类，SMN分布是正态分布灵活的扩展，与正态分布相比，基于SMN分布下的模型更加具有稳健性。关于SMN分布的更多细节参见Andrews和Mallows(1974)，Fang等人(1990)，以及Lange和Sinsheimer(1993)^[11].近期，SMN分布已经被应用于一些特别的测量误差模型，比如，Osorio等人(2009)在SMN分布下研究了Grubbs模型的估计和影响分析^[12]；Lachos等人(2011)研究了在SMN下无重复测量误差模型的估计和影响分析^[13]。另外，Lachos等人(2010)混合尺度偏斜正态分布应用于测量误差模型之中^[14]。在本文中，我们将讨论重复测量误差模型的极大似然估计，该模型中重复观测值一直服从SMN分布。由Pinheiro等人(2001)提出的结构代表使得EM算法可以更好的用于参数估计^[15]。

在最近几十年里，研究人员一直都非常重视统计模型中参数估计稳健性方面的评估。例如减少个体观测点后，研究参数估计受到的影响，是用来检测强影响点或异常值点最常用的技术(见Cook和Weisberg 1982^[16]; Lindley 1972^[17]).然而，近几年来在模型或数据中有较小扰动的影响性分析已经受到越来越多的关注，局部影响分析是一种常见的统计方法，用于评估参数估计的稳健性。随着Cook(1986)^[18]开创性工作的展开，近几年Galea-Rojas等人(2005)^[19]和Osorio等人(2007)^[20]，以及其他统计研究者已经在该研究领域作出了很多研究成果。然而，SMN-MEM的对数似然函数涉及到积分，由于这些方法将涉及到函数的一阶和二阶导数，所以直接运用Cook关于SMN-MEM的研究成果是非常困难的。近年，Zhu和Lee（2001）提出了对带有缺失数据的统计模型进行局部影响分析的方法，通过对Q函数进行处理分析，即EM算法中第E步的完全数据对数似然函数的条件期望^[21]。V.H.Lachos,T.Angolini和C.A.Abanto-Valle把Zhu和Lee影响分析的理论应用于SMN-MEM上，提出了重尾分布下测量误差模型的局部影响分析^[22]。

本文将按以下结构进行分析。在第二节中，为了结构的完整性，我们将对正态混合尺度分布(SMN)进行介绍。在第三节中，我们将定义重尾分布下重复测量误差模型(SMN-RMEM)，并给出EM算法的概括性介绍，再利用EM算法进行极大似然估计。在第四节中，在不完全数据模型下，给出局部影响分析的介绍并推导出在SMN-RMEM下进行局部影响分析所需的公式，将在3种扰动模型下进行分析。在第五节中，我们将应用局部影响分析方法对真实数据展开分析。最后，在第六节中，给出总结性结论。

二、正态混合尺度分布

正态混合尺度分布对于统计模型是十分重要的，可以将其定义为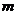维自由向量

剩余内容已隐藏，请支付后下载全文，论文总字数：19759字

相关图片展示：