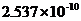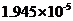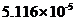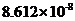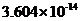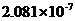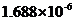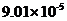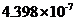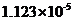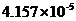论文总字数:31838字
目 录
- 引言....................................................5
- 数据分析与处理..........................................5
2.1数据导入..............................................................5
2.2相关性检验............................................................6
2.3数据进行对数变换......................................................6
3.回归分析................................................7
3.1模型的构建............................................................7
3.2对2006年数据构建回归方程.............................................8
3.3对2007年数据构建回归方程............................................10
3.4对2008年数据构建回归方程............................................13
3.5对2009年数据构建回归方程............................................14
3.6对2010年数据构建回归方程............................................16
3.7对2011年数据构建回归方程............................................18
3.8对2012年数据构建回归方程............................................20
3.9对2013年数据构建回归方程............................................21
3.10对2014年数据构建回归方程...........................................23
3.11对2015年数据构建回归方程...........................................24
- 聚类分析...............................................26
- 时间序列分析...........................................28
- 结论...................................................30
参考文献.................................................31
附录.....................................................32
- 引言
近年来,随着住房问题的关注度越来越来,房价成为了一个广泛关注的社会问题,经济问题。但是由于炒作哄抬房价等不良行为,使得某些地方的房价不随社会发展内在规律控制,一度往上飙升,甚至出现天价房等不正常事件。因此,找出房价与各个相关因子间的关系,得到一个不受炒房等不良行为影响,仅和市场规律变化有关的理性价格势在必行。沈英英 通过线性回归对房地产价格影响因素进行建模分析;李曦和汪淋媛
通过线性回归对房地产价格影响因素进行建模分析;李曦和汪淋媛 通过层次分析模型对房屋因素,生活因素和其他因素建立定性模型;秦迎霞等人
通过层次分析模型对房屋因素,生活因素和其他因素建立定性模型;秦迎霞等人 通过多元线性回归对房地产价格进行分析建模;郭生南
通过多元线性回归对房地产价格进行分析建模;郭生南 通过对房地产价格建立多元回归模型实现对其的分析。刘红勇
通过对房地产价格建立多元回归模型实现对其的分析。刘红勇 等人通过岭回归法对四川省的房地产价格进行分析;马世骁和高梦瑶
等人通过岭回归法对四川省的房地产价格进行分析;马世骁和高梦瑶 通过多元回归分析法对沈阳市房地产价格预测;吴敏
通过多元回归分析法对沈阳市房地产价格预测;吴敏 以广东省为例通过多元回归法对影响房地产价格的因素进行分析;梁浩和杨光宇
以广东省为例通过多元回归法对影响房地产价格的因素进行分析;梁浩和杨光宇 通过回归分析和傅里叶级数分析得到关于武汉的房地产模型;洪增林等人
通过回归分析和傅里叶级数分析得到关于武汉的房地产模型;洪增林等人 通过主成分回归分析对西安的房地产走势进行预测;陈微微
通过主成分回归分析对西安的房地产走势进行预测;陈微微 通过多元回归分析和灰色关联度分析对岳阳市房地产影响因素进行分析;Huixuan Zhang
通过多元回归分析和灰色关联度分析对岳阳市房地产影响因素进行分析;Huixuan Zhang 等人以吉林市为例对房地产价格影响因素研究进行回归分析;Hui Zhi
等人以吉林市为例对房地产价格影响因素研究进行回归分析;Hui Zhi 等人通过ARMA模型对西安的住房价格影响因素进行研究;Han Dengli
等人通过ARMA模型对西安的住房价格影响因素进行研究;Han Dengli 等人通过多元线性回归模型对房地产价格进行预测。但是他们都是将全国的数据作为一个整体进行分析,由于中国东部和西部发展水平差别大,大城市与小城市间发展水平差别大,使得他们得到的回归模型并不适用于中国每一个省市,只能得到一个平均值或者仅研究单独的某一地区,使得到的结果不能处处适用。因此本文对此做出改进,根据每一个省每一年的数据,根据找出各省的理性价格将不同等级的房地产价格分别开来,再分别对不同等级的房地产理性价格进行时间序列分析,以得到较为准确的趋势变化。
等人通过多元线性回归模型对房地产价格进行预测。但是他们都是将全国的数据作为一个整体进行分析,由于中国东部和西部发展水平差别大,大城市与小城市间发展水平差别大,使得他们得到的回归模型并不适用于中国每一个省市,只能得到一个平均值或者仅研究单独的某一地区,使得到的结果不能处处适用。因此本文对此做出改进,根据每一个省每一年的数据,根据找出各省的理性价格将不同等级的房地产价格分别开来,再分别对不同等级的房地产理性价格进行时间序列分析,以得到较为准确的趋势变化。
2.数据分析与处理
2.1数据导入
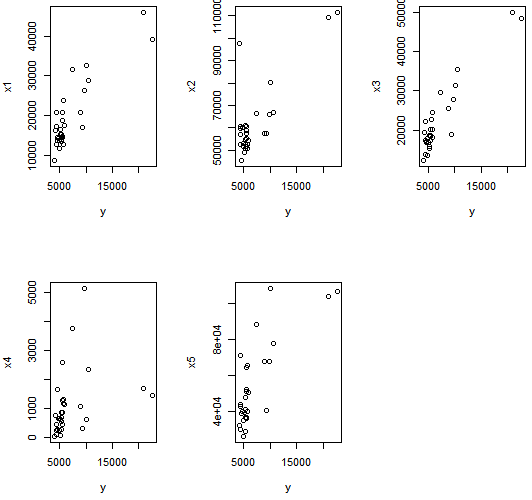
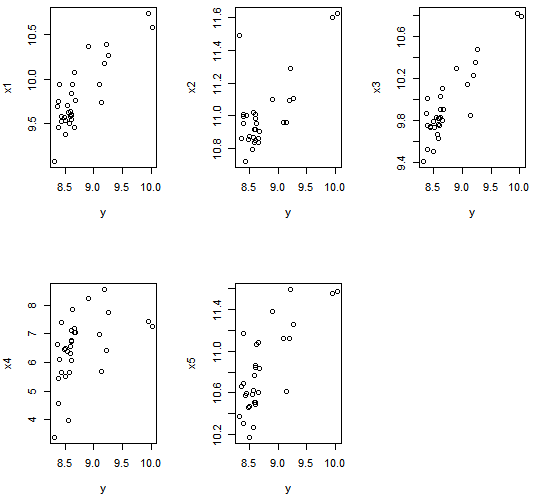
利用国家统计年鉴,分别获得了2006年至2015年总共十年的31个省市自治区的六个指标的具体值,并分别令因变量y为商品房平均销售价格(元/平方米),自变量x1为居民消费水平(元),x2为城镇单位就业人员平均工资(元),x3为居民人均可支配收入(元),x4为房地产增加值(亿元),x5为人均地区生产总值(元/人)。表1为2015年的部分数据,作为范例进行说明。
表1 2015年31个省市自治区商品商品房平均销售价格和各因素的量化数值(部分)
省份 | 商品商品房平均销售价格 | 居民消费水平(元) | 城镇单位就业人员平均工资 | 居民人均可支配收入 | 房地产业增加值 | 人均地区生产总值 |
北京省 | 22633 | 39200 | 111390 | 48457.99 | 1438.43 | 106497 |
天津省 | 10107 | 32595 | 80090 | 31291.36 | 618.25 | 107960 |
河北省 | 5759 | 12829 | 50921 | 18118.09 | 1313.62 | 40255 |
山西省 | 4870 | 14364 | 51803 | 17853.67 | 639.07 | 34919 |
内蒙古自治区 | 4441 | 20835 | 57135 | 22310.09 | 441.37 | 71101 |
... | ... | ... | ... | ... | ... | ... |
2.2相关性检验
再进行回归分析建模之前,由于数据的多元性,本文有必要分别对2006年至2015年十年的数据进行相关性检验,确保所选变量与因变量y确实存在相关性。本文将通过三种相关检验pearson检验,kendall检验和spearman检验来进行确认。通常使用pearson相关系数来表示变量间的线性相关程度;kendall相关系数通常用来衡量变量间的等级相关程度;而spearman相关系数一般用来衡量定序变量之间的相关度。通过相关性检验可分别得到2006年至2015年每一年的三种相关性检验均通过,各个自变量和因变量都相关。本文以2015年的相关性检验为例进行说明。
表2 2015年各自变量和因变量的相关性检验
pearson检验 | kendall检验 | spearman检验 | ||||
商品房平均销售价格 | P值 | 相关系数 | P值 | 相关系数 | P值 | 相关系数 |
居民消费水平 | 0.8680665 | 0.5182796 | 0.6733871 | |||
城镇单位就业人员平均工资 | 0.79601 | 0.02625 | 0.2817204 | 0.0428 | 0.3673387 | |
居民人均可支配收入 | 0.9303892 | 0.6129032 | 0.7709677 | |||
房地产业增加值 | 0.07976 | 0.3195069 | 0.4795699 | 0.000141 | 0.6419355 | |
人均地区生产总值 | 0.7687106 | 0.5311828 | 0.6794355 | |||
从表2可以看到在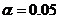 下各自变量和因变量的三种相关性检验的P值均小于0.05,均通过了检验,说明各个自变量和因变量是相关的。
下各自变量和因变量的三种相关性检验的P值均小于0.05,均通过了检验,说明各个自变量和因变量是相关的。
- 3数据进行对数变换
由于商品房平均销售价格的理性售价是一个十分复杂的因素,因此不能仅用一个简单的函数表达式来表达。而多元回归分析法可以通过一系列数学计算找到一个经验回归函数对目标进行拟合。因为回归函数符合多元线性相关模型的几率很低,这使得多元非线性回归模型是有效的。即y的值等于所有自变量x做关于对应b的指数运算之后的n个乘积再乘以参数A。由于多元非线性回归模型无法估计待定参数,需要将非线性模型拆分转化成线性模型计算。这样既准确又方便计算。 由于每年的数据分布相差不大,以2015年的数据为例进行说明。
由于每年的数据分布相差不大,以2015年的数据为例进行说明。
剩余内容已隐藏,请支付后下载全文,论文总字数:31838字
相关图片展示:
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;