论文总字数:15802字
目 录
1.引言 1
1.1 选题意义 1
1.2 国内外研究现状 1
1.3 研究内容 2
2.聚类算法比较 2
2.1 传统聚类算法 2
2.1.1 k-means算法 2
2.2 基于模型聚类算法 3
2.2.1 k中心函数聚类算法 3
2.2.1 线性混合样条模型(lmms) 5
3.数据介绍 6
3.1 数据来源 7
3.2 数据说明 7
4.聚类算法实例分析 7
4.1 k-means聚类 7
4.2 k中心函数型聚类 9
4.2.1 k-centers FC初始聚类 9
4.2.2 k-centers FC迭代聚类 10
4.3 基于lmms聚类 11
4.4 聚类质量评价 12
4.4.1 聚类谱图分析 12
4.4.2 相似性度量 13
4.4.3 CV准则评判 13
5.讨论 14
6.结论 14
参考文献 15
致谢 16
基于基因表达数据的函数型数据聚类方法分析
周颖
, China
Abstract:Cluster analysis is an important analytic method for gene expression data. Because the traditional multivariate clustering method can not grasp the characteristics of gene in the study of gene expression data, a number of novel clustering methods based on functional data have emerged.
In this paper, we analyze and compare the k-mean, k-centers function clustering and linear mixed spline models which are mainstream function clustering methods. And the difference of clustering effect of these methods is discussed by yeast gene expression data. It is found that the functional clustering method has a robust advantage in dealing with gene expression data, and the clustering method based on linear mixed spline model has better performance than other clustering methods in the case of data loss and high dimension.
Key words:Gene expression data;K-mean clustering;K-centers functional clustering; Linear mixed model splines
1引言
1.1选题意义
随着基因芯片技术和生物技术的迅速发展,产生了大量的基因表达数据。时间过程基因表达研究涉及随时间重复测量数千个基因的表达水平,因而导致极高维的数据。这些基因数据往往是在时间序列上选取多个截面,再在截面上的同一时间点下选取样本观测值所构成的样本数据。在数据空间中表现出函数性的特征,并具有数据量大,维数高的特点。因而如何对这些数据进行有效分析,认识其中的本质,从中挖掘出有用的生物学信息是目前研究的重点[1] 。聚类是目前基因表达数据分析的主要技术之一,能将功能相关的基因按表达谱的相似程度归纳成功能表达类别。鉴于聚类在基因表达数据分析中的广泛应用,根据聚类数目的不同而选择合适的聚类方法来应用于基因表达数据聚类中,这对研究者来说是至关重要的。
1.2国内外研究现状
多元聚类方法像k-均值聚类[2],层次聚类,自组织图上的聚类,有限混合模型,模糊平均聚类和紧密聚类等都有利于降低基因表达数据的维数,并鉴定共表达基因和共调节基因组。这些常规聚类算法经常应用于纵向数据,例如生长曲线,重复测量的基因表达谱和许多其他数据集。但由于时间过程基因表达研究涉及随时间重复测量数千个基因的表达水平,因而导致极高维的数据。上述方法将每个基因的测量序列作为不同点的载体处理,因此序列元件的任意排列不会影响聚类结果。然而,在时间过程基因表达研究中,需要着重考虑数据的时间排序以及获得的相应聚类。此外,时间过程基因表达数据表现出诸如缺失值,不等的取样时间或较大的测量误差等问题[3]。上述提到的许多技术在处理缺失值方面存在困难,并且对所有基因需要相同的取样时间,又或者不能解释随着时间的推移在相同基因上进行的测量之间的相关性,因而不能较好地抓住基因特征。
近年来,已经出现利用函数型特性的聚类方法来研究基因表达数据。国内外知名的统计学者就函数型数据做了许多的研究,也取得很多有价值的成果。如Song等[4]提出一种基于函数型数据分析(Functional Data Analysis,简称FNDA)来聚类时间过程基因表达谱的方法。通过FNDA设置来解决聚类问题,该方法使用基函数扩展来描述随时间变化的基因表达曲线。又由于基于聚类的系数必须为所有聚类选择相同的基函数,以使用拟合的系数作为聚类指标。这可能产生一些困难,因为必须选择适当的基函数,使得拟合的系数可以充分地反映聚类差异。因而Chiou和Li[5]提出一种用于纵向数据的函数型聚类方法:k中心函数聚类算法(k-centers FC),考虑聚类间的变化差异的平均值和模式,以预测聚类成员,且证明了在可识别性条件下,k-centers FC提出与传统的聚类算法相比可以大大提高集群质量。Coffey等[3]提出一种方法来研究函数型数据。该方法利用线性混合效应模型和P样条平滑来同时平滑基因表达数据,目的是消除任何测量误差/噪声,并使用混合效应模型的有限混合来聚类表达谱。这种方法具有许多优点,包括减少计算时间以及在标准软件包中更容易实现。Straube等[6]提出一个模型框架来处理时间过程“组学”数据,利用线性混合模型样条(Linear Mixed Model Splines,简称lmms)框架来对函数型数据进行建模。在框架中建模每个分子表达谱,其考虑受试者特异性。通过序列选择最佳模型,并使时间序列数据的维度降低。该框架具有高度灵活的数据驱动方法,旨在建模随时间可能不同的噪声水平和轨迹的海量数据。它不仅可以处理缺失值,具有低计算量,而且可以避免任意输入参数。郭均鹏等[7]在对传统聚类算法研究基础上,首次提出将导函数距离引入函数型数据的聚类中,设计了函数型数据的分步系统聚类算法。由于函数型数据的稀疏性和无穷维特性使得传统聚类分析失效,王德青等[8]在界定函数型数据概念与内涵的基础上提出一种自适应迭代更新聚类分析。汪雪红[9]提出一种结合有损数据压缩的双聚类算法,将其应用于基因表达数据中,从而挖掘出更多和更高生物学价值的基因。岳超[10]为深入了解大豆疫霉引起的大豆病害,在基因芯片试验数据分析中通过聚类分析以及基因网络构建来深入挖掘出大豆遗传育种的信息。
1.3研究内容
现有的基于函数型的聚类方法存在许多差异,如k-centers FC[5]在可识别性条件下,与传统方法相比可以极大地提高聚类质量。又有通过线性混合效应模型和P样条平滑[3]的结合来处理纵向数据,从而更好地拟合时间过程基因表达数据。又有如线性混合效应样条模型(lmms)[6]考虑受试者特异性来建模每个分子表达谱。并通过序列模型选择方法选择最佳模型,并使时间序列数据的维度降低。
因而本文期望比对一种传统的聚类方法(k-均值聚类法)与两种函数型聚类方法(k-centers FC与基于lmms的聚类方法),通过将方法运用到酵母基因表达数据中来比较不同聚类方法在应用到函数型数据上的差异性能规律。本文的其余部分概述如下:第2节介绍三种方法的基本原理和理论性质。第3节对数据进行简要介绍。第4节中将方法运用于酵母基因表达数据,并对聚类质量进行分析。第5节和第6节分别是对结果的讨论和文章总结。
2聚类算法比较
2.1 传统聚类算法
2.1.1 k-means算法
k-means算法是典型的基于距离的聚类算法,其采用距离作为相似性的评价指标,当两个对象的距离越近,则相似度就越大。该算法认为簇是由距离相近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。
2.1.1.1 k均值算法流程
令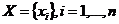 是n个d维点的集合,被聚成K个簇的集合,
是n个d维点的集合,被聚成K个簇的集合,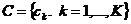 。 K-means算法找到一个分区,使得集群的经验均值与集群中的点之间的平方误差最小化。让
。 K-means算法找到一个分区,使得集群的经验均值与集群中的点之间的平方误差最小化。让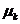 成为群集
成为群集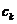 的平均值。
的平均值。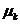 和簇
和簇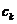 中的点之间的平方误差定义为:
中的点之间的平方误差定义为:
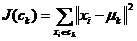 (1)
(1)
K均值的目标是使得所有K个簇上的平方误差的总和最小化,
剩余内容已隐藏,请支付后下载全文,论文总字数:15802字
相关图片展示:
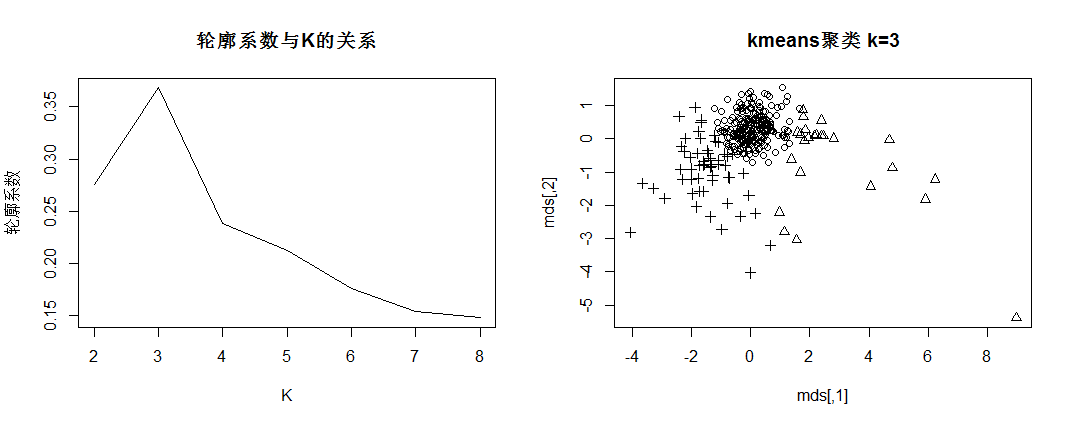
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


