论文总字数：29970字

摘 要

国内金融市场的日益完善加快了利率市场化的进程。为迎合这样的变化，利率和金融基础工具的理论也需要进一步的发展。为此，本文主要探究了利率期限结构模型并应用到折现债券的定价。

首先，本文阐述了利率期限结构在债券定价中的基准作用以及利率期限结构传统理论和现代模型的发展。然后，基于Vasicek模型和Cox-Ingersoll-Ross模型作折现债券定价方程的推导。再向Vasicek模型引入跳跃大小服从非对称双指数分布的跳跃项建立了跳跃-Vasicek模型，并基于此模型推导出来折现债券定价方程。最后，利用银行间7天回购利率作实证分析。实证分析表明，上述三种模型可以比较好地刻画利率的变动趋势。新建立的跳跃-Vasicek模型较为准确地刻画利率的跳跃行为，但是用作仿真时会模拟出异常值。基于这三个模型的定价结果与实际报价的误差不大，这表明这样的债券定价方程可以体现折现债券的内在价值。

关键词 Vasicek模型 Cox-Ingersoll-Ross模型 跳-扩散模型 债券定价

The Term Structure of interest rate and the research of bonds pricing

Abstract

The improvement of the domestic financial market accelerates the process of interest rate liberalization. To satisfy this, interest rates and financial tools basic theory also need further development. Therefore, this dissertation mainly analyses the term structure of interest rate model and its application on the discount bond pricing.

Firstly, this dissertation shows that the term structure of interest rate theory is the benchmark of the bond pricing and that how the traditional and modern theories develop. After this, discount bond pricing function is deduced based on the Vasicek model and Cox-Ingersoll-Ross model. The jump-Vasicek model, which has a jump term obeying the asymmetric double exponential distribution, is created and used to deduce a discount bond pricing function. In the last part of this dissertation, we provide an empirical analysis of 7 day repo rate between banks. According to the empirical analysis, it can be found that the jump- Vasicek model can accurately depict the jump behavior interest rates, but it sometimes simulates some abnormal values. The discount bond pricing results basing on three models mentioned above are very close to the real market prices, which means that pricing function deduced from these models can reflect the intrinsic value of the discount bond.

Keywords:Vasicek model; Cox-Ingersoll-Ross model; Jump-diffusion model; Bond pricing

目录

摘要 I

Abstract II

插图索引 IV

表格索引 IV

第一章 绪论 1

1.1.研究背景及意义 1

1.2.国内外研究现状 1

1.2.1.单因素模型 2

1.2.2.多因素模型 2

1.2.3.跳跃模型 2

1.3.本文内容安排 2

第二章 利率期限结构的理论基础 3

2.1.传统的利率期限结构理论 3

2.1.1.预期理论 4

2.1.2.流动性溢酬理论 4

2.1.3.市场分割理论 4

2.1.4.期限偏好理论 5

2.2.现代的利率期限结构理论 5

2.2.1.均衡模型 5

2.2.1.1.单因素模型 5

2.2.1.2.多因素模型 7

2.2.1.3.跳跃模型 7

2.2.2.无套利模型 8

第三章 利率期限模型与债券的定价 9

3.1.基于Vasicek模型和Cox-Ingersoll-Ross模型的债券定价 9

3.1.1.基于Vasicek模型的债券定价 10

3.1.2.Cox-Ingersoll-Ross模型的推导 11

3.2.基于带跳跃项的Vasicek模型 11

3.2.1.跳跃项的统计性质描述 11

3.2.2.跳跃模型的债券定价方程 12

第四章 折现债券定价模型的实证研究 14

4.1.数据 14

4.1.1.银行间7天回购利率数据描述 15

4.1.2.债券数据描述 16

4.2.参数估计的实现方法 17

4.3.利率期限结构模型的参数估计结果 18

4.4.折现债券的定价结果 20

第五章 结论 21

参考文献 22

致谢 23

附录 23

插图索引

Figure 1利率期限结构模型分类 1

Figure 2利率期限结构的形状 3

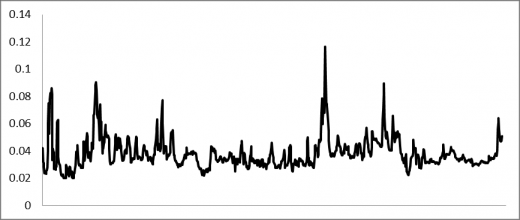
Figure 3 2011年至2014年银行间七天回购利率走势图 15

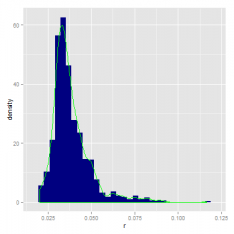
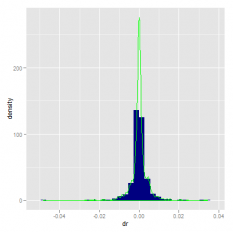
Figure 4 银行间7天回购利率其一阶差分频率直方图 16

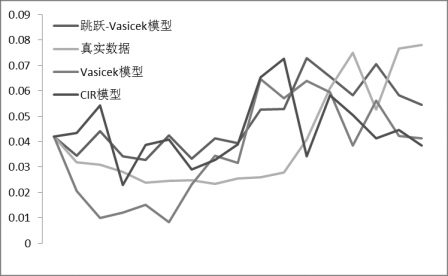
Figure 5 真实数据和各个模型的仿真结果比较 19

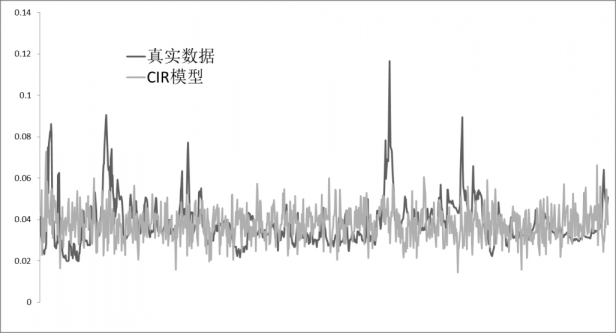
Figure 6 真实数据和跳跃-CIR模型的仿真结果比较 19

表格索引

Table 1利率及其一阶差分的描述统计量 15

Table 2 研究的贴现债券信息表 17

Table 3 参数估计的结果 18

Table 4 贴现债券的定价结果 20

Table 5 三个模型的定价结果误差比较 21

Table 6 计算误差和期限、利率的关系 21

绪论

• 1. 研究背景及意义

当政府、金融机构或企业想筹集资金的时候，它们其中一种选择是以借债的形式筹集。一般来说，它们承诺按照协商好的利率支付投资者应得利息，并按照约定归还本金。而这样的向投资者做的承诺会以发行债权债务凭证呈现，这个凭证就是一般说的债券。人们一般除了关注除了债券带来的定期的或不定期的利息收入，人们还会关注价格的变动趋势。这是因为债券价格因为各种因素而变动，人们可以买涨或是卖空债券赚取利润。因而，债券定价模型受到了很多研究者的关注，且相关的模型一直在更新和拓展。

金融数学中债券定价模型相比传统模型更关注各种不确定因素的影响。而其中一个重要的因素便是利率。有一点值得注意的是，债券的收益利率是与市场上某些特定的利率相关的。比如，浮动利率债券的利率大小就是由某一个基准利率的和既定的利差决定的。这个基准利率可以是各种与市场整体收益率水平要有较强的相关性且波动不定的利率，比如1年期定期储蓄存款利率、银行间同业拆放利率等。而由于贴现债券或者零息票债券是折现发行的，其的收益率也往往和这些基准利率有较强强相关性。

而主流观点认为期限是影响利率大小变化的重要因素，所以期限会是利率理论的研究重点。而表现某一个特定时间点的期限和利率关系的曲线就是所谓的利率期限结构。而债券定价方程式也是在描述债券的收益利率与其到期期限之间的关系^[[1]]。又因为债券价格是与利率的变化相关，它们之间函数关系是确定的，所以要构建的债券定价模型，需要研究的是利率期限结构模型。

• 1. 国内外研究现状

本文主要研究的是利率期限结构模型，并将其成果应用到债券定价方程的推导中。根据利率期限结构理论的研究进程，相关的研究可分为：传统利率期限结构理论和现代利率期限结构理论。收益率曲线的形态特征、特征的意义和曲线成因是传统理论的关注重点。现代理论则着眼于利率期限结构变化的动态过程，而这是本文研究的重点。下面Figure 1 是利率期限结构模型的研究概况。

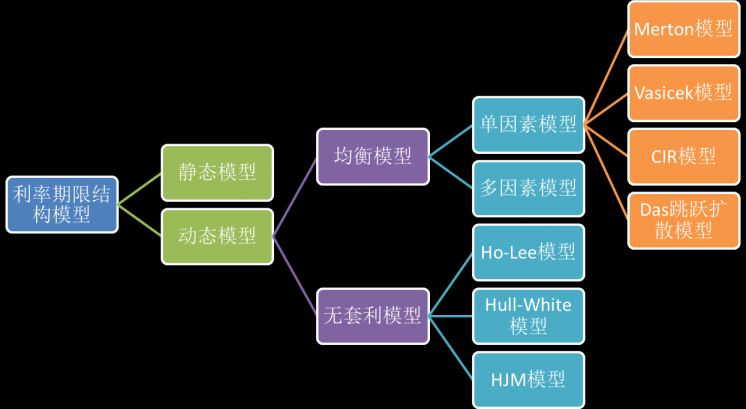
Figure 1利率期限结构模型分类

• • 1. 单因素模型

动态利率期限结构模型的研究开始于二十世纪七十年代。在Merton应用随机微分方程来描述利率的动态变化过程之后，这方面的研究就逐渐开始。Vasicek（1977）[1]提出了可以描述了利率的会围绕某个值上下波动的特征的单因素模型。这个模型与其他模型相比较为简单，描述利率的主要参数都是常数。尽管如此，Vasicek模型在实际应用中还是有用处的，这一点体现在它的拟合结果比较优质。但是，这个模型有一个缺陷是：模拟仿真模拟的结果会出现负数，这与利率恒大于零的实际情况是不相符的。Cox、Ingersoll、Ross（1985）[2]提出的利率的方差和利率平方根成正比的模型则避免了上述问题，此模型简称CIR模型。根据推导过程分类，除了上述的均衡模型，还有基于无套利假设所构建的模型。比如Ho和Lee（1986）[3]提出的模型，就是一个基于上述假设但是不具均值回复性的二项式的Vasicek模型。以上提及的都是仿射模型，除此之外，还有Black、Derman和Toy（1990）[4]以及Black和Karasinski（1991）[5]等提出的非仿射模型。

• • 1. 多因素模型

单因素模型一般只有瞬时利率是随机变动的，不足以很好的描述受到多个因素影响的利率的变动过程，因此研究学者以单因素模型为基础又提出多因素模型。Longstaff和Schwartz（1992）[6]构建了以短期利率和短期利率变化的方差为因素两因素模型.Hull和 White（1994）[7]提出了以短期利率和长期均值为因素的两因素Vasicek模型。Balduzzi(1996)[8]还提出加入波动水平作为考虑因素构建了三因素模型。

• • 1. 跳跃模型

金融市场不是一直保持平稳的，偶尔会因为异常事件而波动。这些异常事件可能会使得利率快说的上升或者下降。上述的模型就不能够很好地描述如股市大幅度波动、金融危机、货币政策调整等信息对利率变化的影响。而有研究发现经济信息能促使利率跳跃行为的发生。Baz和Das（1996）[9]计算出了跳-扩散利率期限结构动态模型的解。Das（2002）[10]提出了一类描述美联储利率变化的泊松-高斯模型，证明了这类模型可以很好的描述短期利率的统计特征以及理解一些市场现象。童汉飞和刘宏伟（2006）[11]利用沪市和深市的股票数据，证明了跳-GAERCH模型可以很好地估计股票收益率和波动率的跳跃性质，这对结构相似的利率跳跃模型的研究也有实质意义。刘凤琴和戈晓菲（2009）[12]用极大似然估计法完成遵循跳-扩散模型的利率模型的参数估计，以及用蒙特卡罗法模拟了存款和贷款的波动过程。

• 1. 本文内容安排

本论文主要从利率期限结构的理论基础、利率模型与债券定价方程的关系和实证研究三个部分，来研究利率期限结构和债券定价这个课题。

第一章是一个绪论。这一章简要地介绍了在利率市场化的背景下，利率期限结构的动态变化过程的研究在债券定价的研究中起到了基准的作用。同时，这一章回顾了现代利率期限结构理论的发展历程，对一些文献进行了综述。

第二章分别阐述了传统和现代利率期限结构理论的具体内容。其中，传统利率期限结构理论的包括了四个重要理论的描述。现代理论期限结构理论的讲述主要基于多个经典的动态模型。

第三章选取了Vasicek模型和Cox-Ingersoll-Ross模型作债券定价公式推导。在为上述两个模型引入跳跃强度服从非对称双指数分布的跳跃项后，再做了新的债券定价方程推导。

第四章对第三章中的利率期限结构模型进行参数估计，将估计的结果应用到债券定价方程和折现债券的实证研究。其中，模型参数估计的部分，本论文采用了MCMC法来实现。

第五章对全文内容作一个总结。

利率期限结构的理论基础

从理论发展进程来看，利率期限结构的理论研究有传统理论和现代理论。传统的利率期限结构理论探究的是收益率曲线的形态特征、这些特征带来的信息和曲线的成因。而现代利率期限结构理论将重心放在描述利率的动态变化过程，其主要内容为各个描述利率变化的期限结构模型。现代理论中的模型还引入了随机微分项来描述利率的动态变化，更能反映市场实际，因而是本论文关注的重点。

剩余内容已隐藏，请支付后下载全文，论文总字数：29970字

相关图片展示：