论文总字数:16741字
摘 要
可靠性理论是以系统寿命特征作为主要研究对象,对产品的寿命进行大量的定量分析的的一门科学,可以说是定量的科学。其诸多的基本概念的定义都是依赖数学术语给出。本文就利用其中的马尔可夫型的相关理论,对2/5(F)可修系统进行了相关的分析和研究。
文中考虑了两种情况。在第一种情况下,假设系统只存在一个修理人员,若同时出现多个部件发生故障,先修关键部件;另一种情况下,假定系统有多个维修工,所有故障部件都可以得到及时的维修,系统转移矩阵可以明确写出。求得概率转移矩阵之后,利用概率论的知识以及求解微分方程组,分别求得系统可靠性的各项指标。
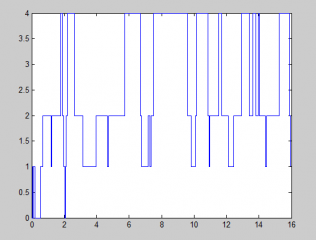
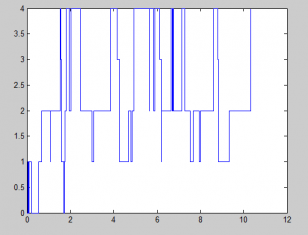
最后,对系统进行数值模拟,在给定参数具体数值的情况下计算出稳态可用度和首次故障前平均时间等可靠性指标的数值解,然后用matlab程序画出系统运行轨线图。最后通过对比,得出“无穷维修工假设下的模型在各方面都略优于只有一个维修工假设下的模型”的结论。
关键词:连续2/5(F)可修系统;可修系统;马尔可夫型;可靠性指标
Reliability analysis for 2-out-of-5 (F) repairable systems
Abstract
Reliability theory is a system features as the main object of study, a science to the life of the product and a large number of quantitative analysis , it should be called quantitative science. Many of its basic concepts are dependent on the definition of mathematical terms. In this paper, the use of the theory of markov model, to 2/5 (F) repairable system analysis and research.
In this study, two cases are considered. In the first model, only one repairman is provided for the system, and it should wait for repair when there are more than one component failed. In another model, sufficient many repairmen are provided so that the failed components all can be repaired immediately. The transition rate matrices are given explicitly. Then we can get these indices by using probability theory and solving differential equations.
Finally, some simulation is provided. Some reliability indices, such as availability and mean time to failure are calculated numerically, and the orbits of system states are also plotted by using Matlab procedure. At last, we got the conclusion that ‘The sufficient many repairmen model is better than only one repairman model’ with comparison of their indices.
Keywords:Continuous 2/5(F) Repairable Systems ; Markov Chain ; Reliability index
目录
摘要 i
Abstract ii
- 引言 1
- 可靠性理论基础 3
2.1 系统可靠性数量指标………………………………………………………………3
2.2 马尔可夫过程定义…………………………………………………………………6
2.3 马尔可夫型可修系统的一般模型理论……………………………………………6
- 连续2/5(F)可修系统的可靠性分析 11
3.1 连续2/5(F)可修系统的定义………………………………………………………11
3.2 连续2/5(F)可修系统的状态分析…………………………………………………13
3.3 只有一个维修工的连续2/5(F)可修系统的可靠性研究…………………………14
3.4 无穷多个维修工的连续2/5(F)可修系统的可靠性研究…………………………20
- 数值模拟 25
- 总结 29
参考文献 30
致谢 31
附录 32
- 引言
在对于诸多系统的可靠性的评估中,可靠性数学,都起到了非常重要的工具的作用。可靠性数学,主要是通过数学中的方法,对所需要评价的系统建立相应的数学模型,并通过数学的手段来对系统的各项指标进行估算。他所涉及的范围非常广泛,包括概率论,随机过程,微分方程,统计和拓扑等诸多的数学领域。通过使用这些数学工具,我们可以实现对系统数据的收集,分析和模型的求解。可以利用其结果指导类似的系统的构建,以实现高效的资源利用。
可靠性是对于产品在一定的条件下,一定的时间内,能够以何种效率完成其对应使命的能力的评价指标。它包含了产品的规定的条件、规定的时间长度、所要实现的功能和完成任务的能力5个因素。其中,时间是可靠性的最重要的评价指标,这个特定的时间是会随着对象的变化而发生改变的,因此,讨论可靠性的重要前提就是确定任务时间。所谓的规定的条件即产品的工作环境条件、使用以及保障条件等。这些条件对产品的可靠性会产生直接的影响,使用时的条件不同,同一产品的可靠性也可能会发生改变。
系统的可靠性分析可以分为不可修系统和可修系统两大类来讨论。从可靠性分析起来的难度的角度来说,不可修系统的分析要相对简单。在讨论不可修系统的可靠性问题时,我们主要运用的是概率论的相关知识。在参考文献[3]中,我们可以看到叶尔哗和白成刚两位就已经对由 n 个部件组成、开关寿命为连续型随机变量的不可修冷、温贮备系统的可靠性的分析。参考其方法,容易掌握对不可修系统的可靠性分析。当问题变为可修系统的可靠性问题时,我们则需要掌握马尔可夫型随机过程的相关知识。这主要是因为在可修的系统中,系统部件的故障和维修的寿命分布往往是服从指数分布且相互之间是独立的,这就导致马尔可夫型在这类系统中有着广泛的应用。在参考文献[4]中,吴清太及叶尔哗就运用了马尔可夫随机过程的相关知识对由两个部件组成的开关寿命为连续随机变量的温贮备可修系统的可靠性进行了分析。当然,现实中还有更多的情况,由于寿命分布不是指数分布,马尔可夫过程的理论是无法适用的。在这种情况下,可修系统的研究就需要另辟蹊径。这种时候我们就需要其他的数学方法来研究这些更为一般的可修系统。在研究非马尔可夫型可修系统时,我们通常可以使用如下的工具:更新过程、马尔可夫更新过程和补充变量方法等等。具体的内容可以在文献[2]中获得详细的介绍。
在文献【1】中,我们可以较为详细的了解各种简单的可修系统的可靠性,其中包括了部件寿命符合指数分布的马尔可夫型可修过程的研究,在指数分布且相互独立同分布的前提假设下,系统的可靠度和平均寿命等指标可以较为简单的通过概率论得到。但是到了实际的应用中,系统会出现各种复杂的组合,除了串联并联等情况以外,还会出现故障条件复杂的模型,比如连续2/5(F)可修系统。这种系统需要连续两个部件出现故障才会导致系统整体瘫痪,所以对系统寿命和故障的发生的求解会相对比较复杂。
在参考文献[1]中,曹晋华老师和程凯老师对可靠性数学的一些基础理论和基本概念进行了详细的介绍。我们可以通过阅读这篇文献,初步熟悉各种常见的需要评价可靠性的系统以及其对应的可靠性的研究方法。从这篇文献中,我们可以学习到串联系统、并联系统、串并联混合系统、表决系统和贮备系统等典型系统的相关理论知识,其中还包括冷贮备、温贮备以及转换开关不完全可靠等贮备系统。从中我们可以对可修系统有个基本的了解,对于其可靠性的分析也可以相应的有所概念,尤其是其对于马尔可夫型系统的研究和分析,对本文的撰写有极大的帮助。在参考文献[5]中,Sarkar.J 和 Li.F 研究了带有 R 个修理设备及 S 个备件的单部件可修系统的可用度特征。其中部件的寿命时间服从具有概率密度函数的分布,部件的修理时间服从指数分布。在参考文献[8]中,Wang K.H.等三人基于系统的可靠度和系统的可用度对四种开关不完全可靠的温贮备系统进行了比较,其中主部件和温贮备部件的寿命时间和修理时间均服从负指数分布。在参考文献[9]中,Zhang Y.L.对带有单个冷贮备及单个修理设备的两同型部件可修系统进行了探索分析。该篇文章中考虑了在每个部件都不能修复如初的条件下的最优替换策略。在参考文献[10]中,Gupta S.M.主要对以下两个可修系统进行了随机分析。第一个系统带有两个同型温贮备部件,部件和系统的故障率均为连续独立的且修理时间是一般分布。第二个系统由三个可修部分组成。三个部分的故障率和修复时间均为连续独立的。系统正常工作假如所有三个部分都在运行,否则系统以一个降低的水平工作直到所有三个部分均失效。
本文会首先介绍一些基本的可靠性指标,介绍这些指标的定义,意义以及简单的推导公式。随后会简单的介绍一下马尔可夫过程,包括其定义,可修马尔可夫系统的一般模型,以及各个可靠性指标的求解公式。之后会对连续2/5(F)可修系统进行介绍和分析,在5个部件独立同分布符合指数分布的假设下,对整个系统的可靠度进行求解。之后还会分别对所有部件都能立即得到维修的情况以及只能一个一个维修的情况作分析,得到对应的指标。
- 可靠性理论基础
2.1 系统的可靠性数量指标
系统,即由多个基本部件组合起来共同完成某种指定的目标的一个整体,这样的整体就是所谓的系统。在可修系统中,除了我们常见的那些用于工作的系统部件,还包括了维修故障所对应的设备。可靠性理论中对于故障的定义如下:产品(部件或系统)丧失规定的功能称为失效或故障。一般,我们将产品的寿命用一个非负的随机变量X来描述,其分布函数为:
 (2.1.1)
(2.1.1)
有了寿命分布F(t),我们可以利用它求得产品在t时刻之前都没有发生故障的概率,以及产品在t时刻依旧正常工作的概率:
 (2.1.2)
(2.1.2)
其中,R(t)被我们称为产品的可靠度。由上述公式可知,R(t)是产品在(0,t]时间段内一直都正常工作的概率。所以产品的平均寿命可以表示为:
 (2.1.3)
(2.1.3)
在产品或系统是可以被修复的情况下,由于有修理的因素存在,产品在故障之后可以经过一段时间被修复,因而可修产品的运行过程中会不断轮换出现系统正常和系统故障,本文将针对这一类问题进行分析和讨论,求解其可靠性的相关指标。
这类产品的可靠性主要指标有:
- 系统第一次出现故障的时间X的分布:
 (2.1.4)
(2.1.4)
剩余内容已隐藏,请支付后下载全文,论文总字数:16741字
相关图片展示:
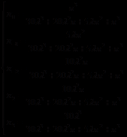
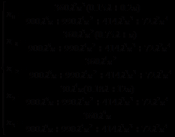
该课题毕业论文、开题报告、外文翻译、程序设计、图纸设计等资料可联系客服协助查找;


